Python OpenCV 影像处理：傅立叶转换

►前言

上篇介绍基于计算影像的梯度，通过在影像中找到梯度值的变化来识别边缘。

本篇将介绍傅立叶变换的基本原理，了解傅立叶变换是如何将影像从空间域转换到频率域的，以及为什么这种转换在影像处理过程中是有用的。以及傅立叶变换的实际应用，展示傅立叶变换在影像去杂讯、影像增强和影像压缩等方面的应用。

并透过程式码的说明，让各位了解OpenCV Python于图像处理上的基本操作。

►傅立叶变换定义

傅立叶变换是一种将讯号从时间域或空间域转换到频率域的数学工具。它可以用来分析各种滤波器的频率特性。对于影像，可以使用二维离散傅立叶变换 (DFT)来寻找频率域。

正弦波讯号 x(t) = A sin(2πft)，可以说  f是讯号的频率，采用其频域可以看到一个尖峰f，如果讯号被取样形成离散讯号，我们会得到相同的频域。也可以将影像视为在两个方向上(x, y )取样的讯号，通过傅立叶变换来分析评频率成分。

一维离散傅立叶变换如下:

 

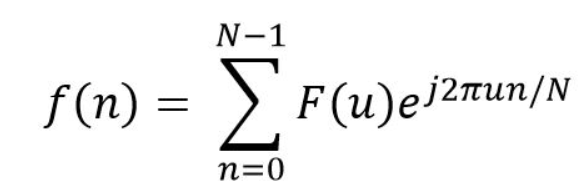
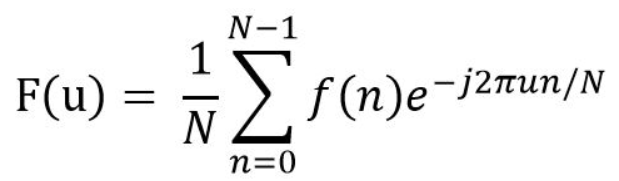
►傅立叶变换定义

OpenCV 提供了 cv2.dft() 和 cv2.idft() 函数来计算离散傅立叶变换（DFT）和逆离散傅立叶变换。这些函数可以用于图像的频域分析和处理。

1.频域