【雷达信号处理】单载频脉冲信号的时宽带宽积推导

前言

只是看到很多地方都有说到单载频脉冲信号的时宽带宽积为1，却没有具体的推导，在这里推导一下试试。

---

一、单载频脉冲信号

令单载频脉冲信号为$f(x)$，那么有$f(x)=g_{\tau }(x)cos({\omega }_{0}x)$，$g_{\tau }(x)$为宽度为$\tau$的门函数，${\omega }_0$为载频。那么具体波形如下。

代码：

tau = 0.02;
w0 = 2000;
t = -0.02:0.0001:0.02;
f = (heaviside(t+0.01)-heaviside(t-0.01));
plot(t,f);
f1 = (heaviside(t+0.01)-heaviside(t-0.01)).*cos(w0*t);
hold on
plot(t,f1,'--');
title('w0 = 2000, 门宽 = 0.2');
xlabel('t');
ylabel('f');

时宽带宽积推导

对$f(x)$利用频域卷积定理，有
$F(j\omega )=\frac{1}{2\pi }{G}_{\tau }(j\omega )\ast \pi (\delta (\omega -{\omega }_0)+\delta (\omega +{\omega }_0))$
即
F ( j ω ) = 1 2 { G τ ( j ( ω − ω 0 ) ) + G τ ( j ( ω + ω 0 ) ) } F(j\omega)=\frac{1}{2}\{G_\tau(j(\omega-\omega_0))+G_\tau(j(\omega+\omega_0))\} F(jω)=21​{Gτ​(j(ω−ω0​))+Gτ​(j(ω+ω0​))}
对于门函数$g_{\tau }(t)$而言，它的傅里叶变换结果$G_{\tau }(j\omega )$为
$G_{\tau }(j\omega )=\tau Sa(\frac{\omega \tau }{2})$
从而
F ( j ω ) = τ 2 { S a ( τ 2 ( ω − ω 0 ) ) + S a ( τ 2 ( ω + ω 0 ) ) } F(j\omega)=\frac{\tau}{2}\{Sa(\frac{\tau}{2}(\omega-\omega_0))+Sa(\frac{\tau}{2}(\omega+\omega_0))\} F(jω)=2τ​{Sa(2τ​(ω−ω0​))+Sa(2τ​(ω+ω0​))}
现在结果很明显了，单载频脉冲函数的频谱就是两个$Sa$函数偏移了${\omega }_0$个单位而已。
$Sa$函数结果如下所示

代码：

tau = 0.02;
w0 = 2000;
w = -20000:0.01:20000;
%%F = tau/2*( ((sin(tau/2*(w-w0)))./(tau/2*(w-w0))) + ((sin(tau/2*(w+w0)))./(tau/2*(w+w0))));
F = tau/2*( ((sin(tau/2*(w-w0)))./(tau/2*(w-w0))));

plot(w,F);
title('单边Sa函数');
xlabel('频率w');
ylabel('F');

带宽仅仅看正频率区即可，所以在上图我只画了右半频率区。带宽计算如下所示。

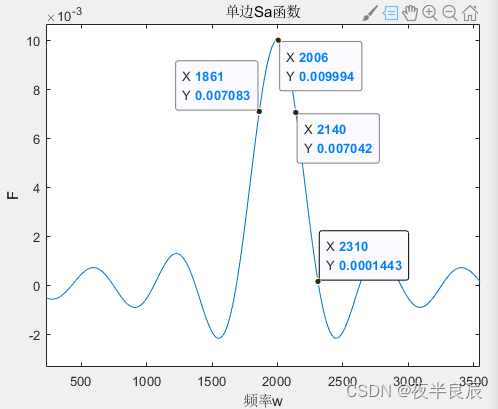
在上课时，我记得老师讲过，$Sa$函数的$-3dB$带宽和主瓣宽度的一般是差不多相等的，也就是$Sa$函数取到峰值和取到$0$之间的距离，虽然优点误差，但是大致误差不超过$10\%(279与304)$。同时载频对带宽并不起作用，于是单载频脉冲信号的带宽就是门函数的带宽。这样就可以利用公式计算，如下，
$Sa(\frac{\omega \tau }{2})=0$，即$\frac{\omega \tau }{2}=\pi$，则$\omega \tau =2\pi$换算成频率，左右同时除以$2\pi$，得$f\tau =1$，此时$B=f-0=f$，所以$B\tau =1$，大致如此。

---

总结

仅仅是自行推导，有问题的话欢迎大家提出。