秒懂二叉树：干掉一棵树

原创已于 2025-09-06 22:48:39 修改 · 918 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

于 2025-07-26 20:58:44 首次发布

c++学习小计专栏收录该内容

2 篇文章

订阅专栏

树在编程中是最疼脑壳的，也是比较难的一块这个数据结构写起来不仅特别复杂，理解起来还有一定的难度，非常非常的不友好，尤其是看到WA。今天就让我们从输了几个方面入手干掉这个大BOSS。

树的简介

数是编程里面一个比较常见的数据结构大致如下图（文字构建）：

A
/ \
B C
/ \ \
D E F

那就让我们先从非常常见的二叉树入手

树的遍历：

1.DLR先序遍历

--- 访问根，其次访问左子树，再访问右子树.

根据刚刚的案例遍历结果是：A,B,D,E,C,F

2.LDR中序遍历

--- 访问左子树，其次访问根节点，再访问右子树.

根据刚刚的案例遍历结果是：D,B,C,A,C,F

3.DLR后序遍历

--- 访问左子树，其次访问右子树，再访问根.

根据刚刚的案例遍历结果是：D,E,B,F,C,A

二叉树

二叉树它有两个分支，每个节点下面都有两个以下及两个子节点，每个节点除根节点外，至少有一个父节点。

我们可以使用一个结构体struct去存一个数：

struct tree {
	int num;   //值
	string s;  //路径
};

tree a[100010];

接下来让我们再定一个函数去判断这棵树是不是个好树如果是一棵好树，那则输出it is a good tree。如果是一棵坏树，那么输出it is a bad tree

一般一棵树是棵坏树，有两种情况:
1.有重复的路径

2.没有父节点

unordered_map<string, bool> path_map; // 用于判断路径是否唯一

// 递归检查树的结构
bool checkGoodTree(int index) {
    if (a[index].s == "") {  // 如果路径为空，说明是叶子节点
        return true;
    }

    // 检查当前路径是否重复
    if (path_map[a[index].s]) {
        return false;
    }

    path_map[a[index].s] = true;  // 标记当前路径已经存在

    // 假设节点的子节点是左右孩子，递归检查左右子树（此部分可以根据实际情况调整）

    return true;
}

例题

1.P1030 [NOIP 2001 普及组] 求先序排列

题目描述

给出一棵二叉树的中序与后序排列。求出它的先序排列。（约定树结点用不同的大写字母表示，且二叉树的节点个数 ≤8）。

输入格式

共两行，均为大写字母组成的字符串，表示一棵二叉树的中序与后序排列。

输出格式

共一行一个字符串，表示一棵二叉树的先序。

输入输出样例

输入 #1复制

BADC
BDCA

输出 #1复制

ABCD

说明/提示

【题目来源】

NOIP 2001 普及组第三题

解析

我们可以使用递归的思想完成一道题，先向左数，进行递归，再向右树进行递归，最后再回溯。

这道题主要考察的是先后变历的顺序

AC CODE

#include <bits/stdc++.h>
using namespace std;
char a[10], b[10];
void dfs(int la, int ra, int lb, int rb)
{
	if (la > ra) return;
	cout << b[rb];
	int p = la, cnt = 0;
	while (a[p] != b[rb]) p++;
	cnt = p - la;
	dfs(la, p - 1, lb, lb + cnt - 1);
	dfs(p + 1, ra, lb + cnt, rb - 1);
}
int main()
{
	cin >> a >> b;
	int len = strlen(a) - 1;
	dfs(0, len, 0, len);
	return 0;
}

是不是非常的简单，看起来非常强大的树，他出题的也就只有那几招。

2.NOT SO MOBILE

题目

Before being an ubiquous communications gadget, a mobile was just a structure made of strings and wires suspending colourfull things. This kind of mobile is usually found hanging over cradles of small babies. The figure illustrates a simple mobile. It is just a wire, suspended by a string, with an object on each side. It can also be seen as a kind of lever with the fulcrum on the point where the string ties the wire. From the lever principle we know that to balance a simple mobile the product of the weight of the objects by their distance to the fulcrum must be equal. That is Wl × Dl = Wr × Dr where Dl is the left distance, Dr is the right distance, Wl is the left weight and Wr is the right weight. In a more complex mobile the object may be replaced by a sub-mobile, as shown in the next figure. In this case it is not so straightforward to check if the mobile is balanced so we need you to write a program that, given a description of a mobile as input, checks whether the mobile is in equilibrium or not. Input The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs. The input is composed of several lines, each containing 4 integers separated by a single space. The 4 integers represent the distances of each object to the fulcrum and their weights, in the format: Wl Dl Wr Dr If Wl or Wr is zero then there is a sub-mobile hanging from that end and the following lines define the the sub-mobile. In this case we compute the weight of the sub-mobile as the sum of weights of all its objects, disregarding the weight of the wires and strings. If both Wl and Wr are zero then the following lines define two sub-mobiles: first the left then the right one. Output For each test case, the output must follow the description below. The outputs of two consecutive cases will be separated by a blank line. Write ‘YES’ if the mobile is in equilibrium, write ‘NO’ otherwise. Sample Input 1 0 2 0 4 0 3 0 1 1 1 1 1 2 4 4 2 1 6 3 2 Sample Output YES

翻译：

递归的方式输入一个树状天平(一个天平下面挂的不一定是砝码还可能是一个子天平)
根据力矩相等原则判断是否平衡。
每个天平的格式读入为W1，L1，W2，L2，当W1或W2为0时，表示该“砝码”实际是一个子天平，接下来会描述这个子天平。当W1和W2均为0时，会先描述左子天平，然后描述右子天平。
子天平的总重量即为原天平的砝码重量。

输入数据组数n，接着将每组天平输入，判断是否平衡。
若平衡则输出“YES”，不平衡则输出“NO”。
每组输出之间有一个空行隔开，注意最后不要输出多余空行。

input

2
1 2 2 2

0 2 0 4
0 3 0 1
1 1 1 1
2 4 4 2
1 6 3 2

output

YES

解析

这道题也是一个非常经典的递归题你要注意一下一个砝码下面可能不是一个砝码，而是一个天平。

AC CODE：

#include <iostream>
using namespace std;

long long read(bool& ok) {
    long long w1, l1, w2, l2;
    cin >> w1 >> l1 >> w2 >> l2; 

    long long lw = w1, rw = w2; 
    if (w1 == 0) lw = read(ok); 
    if (w2 == 0) rw = read(ok); 

    if (lw * l1 != rw * l2) ok = false; 
    return lw + rw; 
}

int main() {
    int n;
    cin >> n; 
    while (n--) {
        bool ok = true; 
        read(ok); 
        cout << (ok ? "YES\n" : "NO\n");

        if (n) cout << "\n"; 
    }
    return 0;
}

看吧！也就是个递归。

3.最后一个就是一个看上去比较难，实际上不是特别难，但代码要敲百行的那种。

题目描述

\color{Gray}\mathsf{Shuchong}Shuchong 给您一个二叉树，您的任务是写一个程序来输出依「阶层（level-order）」遍历的结果。在本问题中，二叉树的每个节点含有一个正整数，并且节点的数目在 [1,256][1,256] 的范围内。

在「阶层」遍历中，依阶层从低到高，同阶层从左到右的次序来列印。

\color{Gray}\mathsf{Shuchong}Shuchong：例如下面这个二叉树的阶层遍历结果就为
5,4,8,11,13,4,7,2,15,4,8,11,13,4,7,2,1

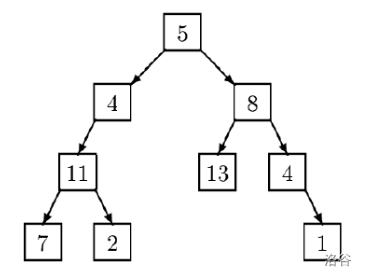
在本问题中，二叉树以节点来表示。每个节点以一个有序数对 (n,s)(n,s) 来表示：

nn 代表此节点的值
ss 代表一个字符串，代表从根节点到达此节点的路径，其中 L 代表左，R 代表右

\color{Gray}\mathsf{Shuchong}Shuchong：比如说上面那个值为 1313 的节点用 (n,s)(n,s) 的表示法就为 (13,(13,RL))，值为 22 的节点用 (n,s)(n,s) 的表示法就为 (2,(2,LLR))，根节点 55 用 (n,s)(n,s) 的表示法就为 (5,)(5,)。

输入格式

首先说明，我们定义 \mathsf{White\ Space}White Space 代表空格或换行符。
输入包含多组测试数据。
每组测试数据为若干节点的集合。各节点间以 \mathsf{White\ Space}White Space 分隔。
注意：在各节点内（也就是左右括号之间）不会有 \mathsf{White\ Space}White Space。当遇到 () 的节点，代表该组测试数据结束。

输出格式

对于每组测试数据，如果输入的节点可以正常的构成一个二叉树的话，请输出按「阶层」遍历的结果。如果输入的节点无法正常的构成一个二叉树的话，也就是说有某些该有的节点没有给，或者重复给（同一个路径上有 22 个节点），请输出 not complete。

输入输出样例 #1

输入 #1

(11,LL) (7,LLL) (8,R)
(5,) (4,L) (13,RL) (2,LLR) (1,RRR) (4,RR) ()
(3,L) (4,R) ()

Copy

C++

输出 #1

5 4 8 11 13 4 7 2 1
not complete

Copy

C++

说明/提示

节点数最少 11 个，最多 256256 个。
建议配合样例自行理解

根据我抄的样例模板，其实可以很快的将这棵树给存下来，但是这道题的输入的确有点逆天。

（在被我的损友险狙了几百下之后，我终于把这道题的题解给写出来了）:
在检测到括号之后，我们就把这个存入到我们的树中再通过sort()的排序检测之后再输出结果

#include<bits/stdc++.h>
using namespace std;
struct node{
	int v,len;
	string s;
}a[10001];
bool cmp(node a,node b){
	if(a.len == b.len) return a.s < b.s;
	return a.len < b.len;
}

int main(){
	string s;
	int cnt = 0;
	while(getline(cin,s)){
		
		int v = 0;
		string ss = "";
		for(int i = 0;i < s.size();++i){
			
			if(s[i] == ')'){

				if(s[i-1] == '('){

					sort(a,a+cnt,cmp);

					bool f = 1;
					for(int j=cnt - 1;j>0;j--){
						if(a[j].s==a[j-1].s) f = 0;
						string save = a[j].s.substr(0,a[j].len-1);
						bool flag = 0;
						for(int k=j;k>=0;k--){
							if(a[k].s == save){
								flag = 1;
								break;
							}
						}
						f=f&&flag;
					}

					if(!f || a[0].s != ""){
						cout<<"not complete\n";
					}else{
						for(int j = 0;j < cnt ; j ++) {
							if(j == cnt - 1){
								cout<<a[j].v;
							}
							else cout<<a[j].v<<" ";
						}
						cout<<"\n";
					}
					cnt = 0;
				}
				else {
					a[cnt++] = {v,ss.size(),ss};
					
				}
				v = 0,ss = "";

			}
			if(s[i] >= '0' && s[i] <= '9') v = v * 10 + (s[i] - '0');
			if(s[i] == 'L' || s[i] == 'R') ss += s[i];
		}
		
	}
	return 0;
}

同时你们的up也祝愿你们

while(true){
    rp++;
    ac++;
    lucky_num++;
}