树与二叉树 | 二叉排序树

二叉排序树简介

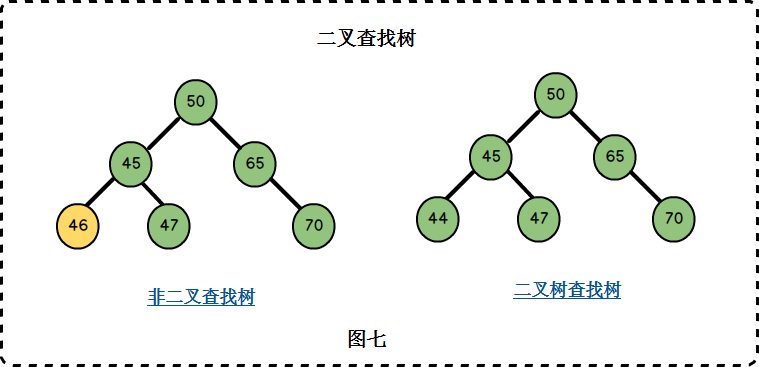
二叉排序树，又叫二叉查找树，它或者是一棵空树；或者是具有以下性质的二叉树：

• 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
• 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
• 它的左右子树也分别为二叉排序树。

二叉排序树的创建

假设我们要为数组 a[] = {62, 88, 58, 47, 35, 73, 51, 99, 37, 93}构建一个二叉排序树，我们按顺序逐个插入元素。

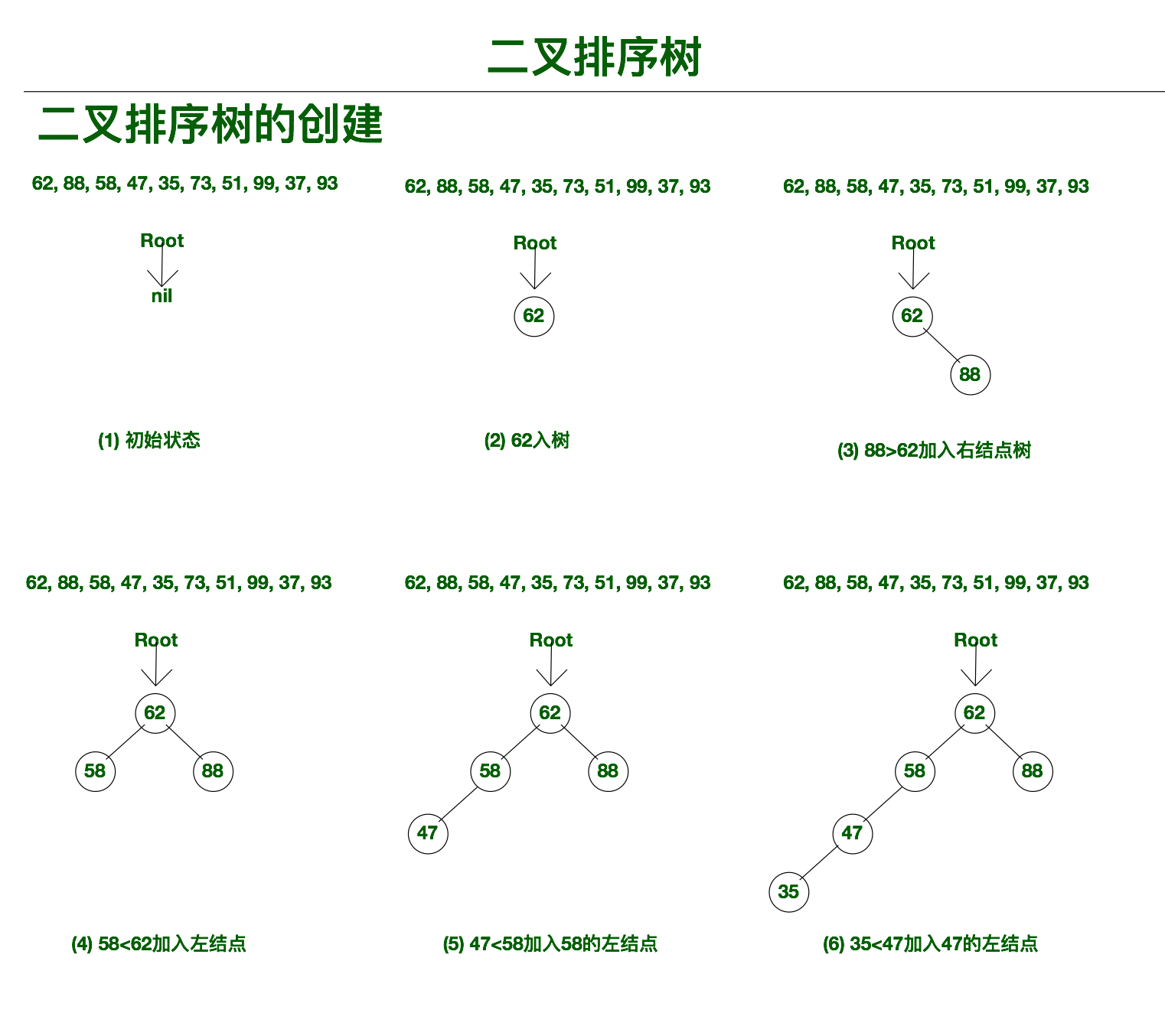
 插入过程是这样的：

1. 在初始化状态下我们二叉排序树的根节点为空，我们依次将集合中的元素通过搜索插入到二叉排序树中合适的位置。
2. 首先在二叉排序中进行搜索62的位置，树为空，所以将62存入到二叉排序树的根节点中，及root=(62)。
3. 从集合中取出88，然后查找我们的二叉排序树，发现88大于我们的根节点62，所以将88插入到62节点的右子树中，即(62)->rchild=(88)。
4. 从集合中取出58，然后从根节点开始查找我们现有的二叉排序树，发现58<62，将55作为62的左结点，即(62)->lchild=(58)。
5. 从集合中取出47，然后对二叉排序树进行搜索，发现47<58, 所以(58)->leftChild=(47)。
6. 从集合中取出35，再次对二叉排序树进行搜索，发现35又小于47，所以(47)->leftChild=(35)。
7. 从集合中取出73，再次对二叉排序树进行搜索，发现62<73<88, 所以有(88)->leftChild=(73)。

以此类推，要做的事情就是不断从集合中取值，然后对二叉排序树进行查找，找到合适的插入点，然后将相应的节点进行插入，具体步骤就不做过多赘述了。

2.1 定义二叉排序节点结构：

1 typedef int DataType;
2 typedef struct Node 
3 {
4     DataType key;
5     struct Node *lchild, *rchild;
6 }BSTNode

 

2.2 代码：

 1 bool InsertBST(BSTNode *&bt, char k)
 2 {
 3     if (bt == NULL)
 4     {
 5         bt = (BSTNode*)malloc(sizeof(BSTN);
 6         bt->key = k;
 7         bt->lchild = bt->rchild = NULL;
 8         return true;
 9     }
10     else if (k == bt->key)
11         return false;
12     else if (k < bt->key)
13         return InsertBST(bt->lchild, k);
14     else
15         return InsertBST(bt->rchild, k);
16 }
17  
18 BSTNode* CreateBST(char A[], int n)
19 {
20     BSTNode *bt = NULL;
21     int i = 0;
22     while(i < n)
23     if (InsertBST(bt, A[i]) == 1)
24     {
25         printf(" 第%d步，插入%d:"，i+1, A[i]);
26         ++i;
27     }
28     return bt;
29 }

 

 

 

二叉排序树的删除

3.1 删除结点为叶子结点

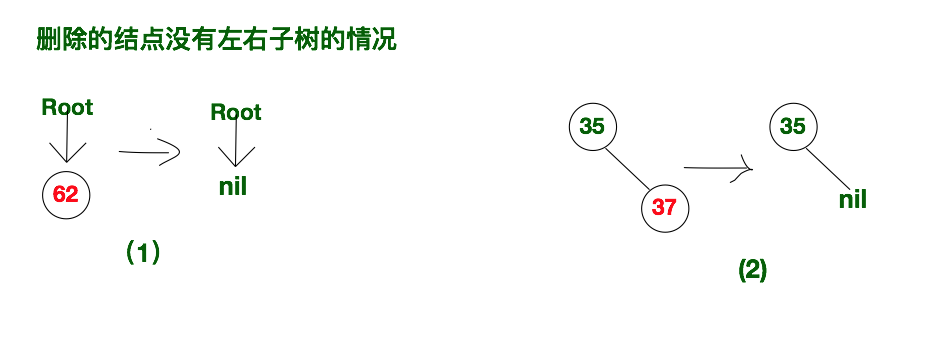
删除的结点没有左子树也没有右子树，也就是删除的结点为叶子结点。这种情况下我们有可以细分为两类:

1. 一种是该叶子结点就是二叉排序树的根节点，也就是二叉排序树中只有一个节点的情况。只需要将root指针置为空即可。
2. 第二种情况是有删除的叶子节点有父节点，直接将父节点连接该删除节点的指针置空即可。

示意图如下所示：

3.2 删除的节点只有左子树的情况

该情况也可以细分为两类：

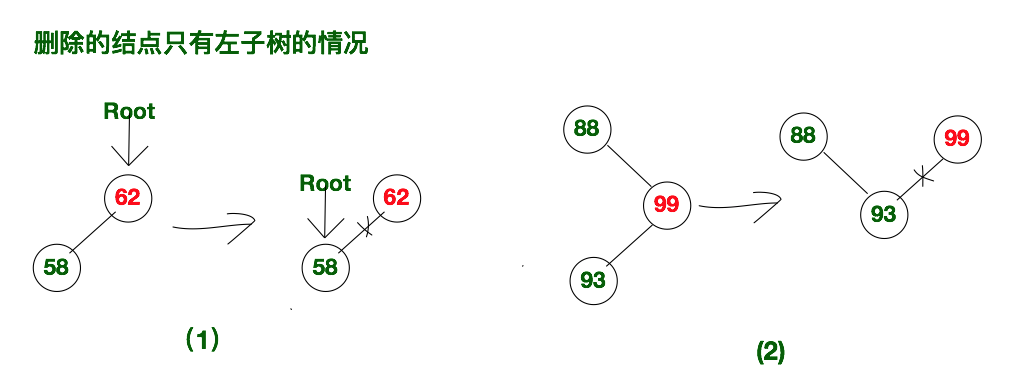
1. 一种是该删除的结点没有父节点，也就删除的节点为根节点，我们需要将根节点的root指针指向即将删除结点的左孩子，然后将删除结点的lchild置空即可。
2. 如果该结点有父节点，那么将父节点相应的孩子指针指向删除节点的左孩子，然后将删除节点的lchild置空。

示意图如下所示：

 

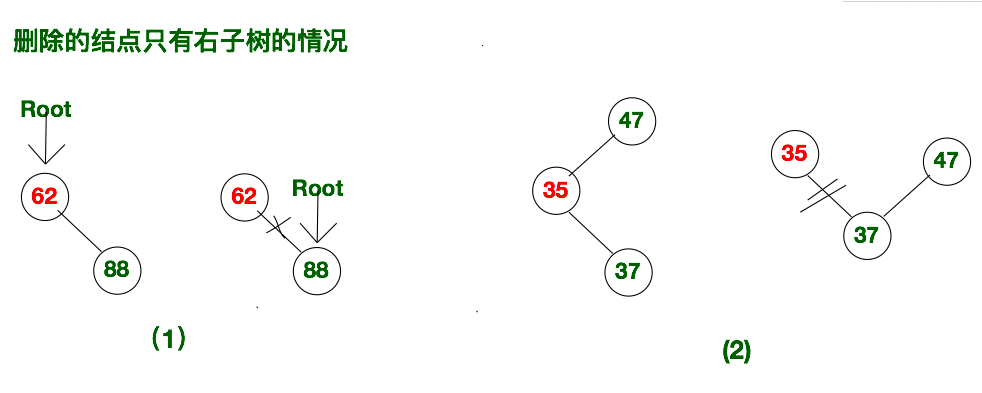
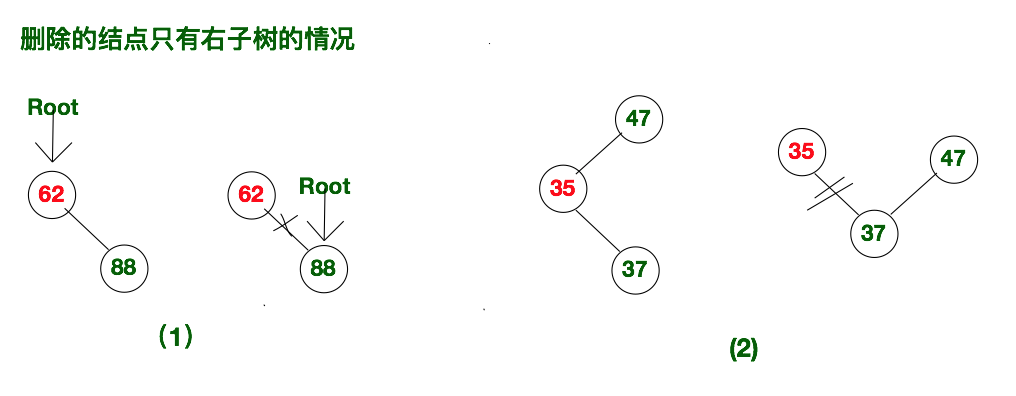
3.3 删除的节点只有右子树的情况

该情况也可以细分为两类：

1. 一种是该删除的结点没有父节点，也就删除的节点为根节点，我们需要将根节点的root指针指向即将删除结点的右孩子，然后将删除结点的rightChild置空即可。
2. 如果该结点有父节点，那么将父节点相应的孩子指针指向删除节点的右孩子，然后将删除节点的rightChild置空。

 示意图如下所示：

 

 

3.4 删除的节点既有左子树也有右子树的情况

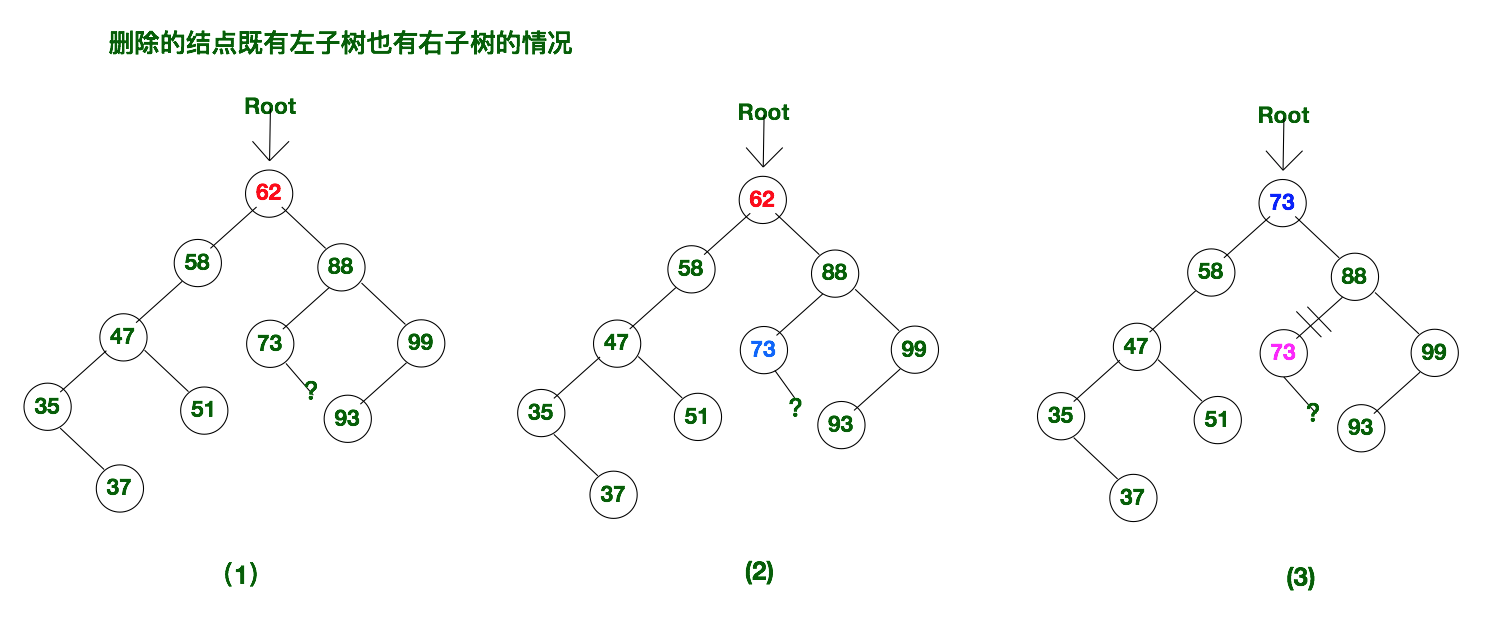
这种情况会稍微复杂一些，我们采用覆盖，再删除的方式进行解决。也就是曲线解决。直接将有左子树也有右子树的结点干掉似乎不是很好实现，因为这样会破坏二叉排序树的结果。我们可以间接的去做。可以分为下方的两步。

• 第一步：查找删除结点右子树中最小的那个值，也就是右子树中位于最左方的那个结点。然后将这个结点的值的父节点记录下来。并且将该节点的值赋给我们要删除的结点。也就是覆盖。
• 第二步：然后将右子树中最小的那个结点(左子树中最大的那个节点也可以)进行删除，该节点肯定符合上述三种情况的某一种情况，所以可以使用上述的方法进行删除。

这样一来我们就间接的删除了既有左子树也有右子树的结点。

具体示意图如下所示：

 3.5 代码：

 1 void Delete1(BSTNode *p, BSTNode *&r)
 2 {
 3     BSTNode *q;
 4     if (r->lchild != NULL)
 5         Delete1(p, r->lchild);
 6     else
 7     {
 8         p ->key = r->key;
 9         q = r;
10         r = r->rchild;  //自己修改的
11         free(q);
12     }
13 }
14  
15 void Delete(BSTNode *&p)
16 {
17     BSTNode *q;
18     if (p->rchild == NULL)
19     {
20         q = p;
21         p = p->lchid;
22         free(q);
23     }
24     if (p->lchild == NULL)
25     {
26         q = p;
27         p = p->rchild;
28         free(q);
29     }
30     else
31         Delete1(p, p->rchild);
32 }
33  
34 bool DeleteBST(BSTNode *&bt, int k)
35 {
36     if (bt == NULL)
37         return false;
38     if (k <bt->key)
39         return DeleteBST(bt->lchild, k);
40     else if (k >bt->rchild)
41         return DeleteBST(bt->rchild, k);
42     else
43     {
44         Delete(bt);
45         return true;
46     }
47 }

 

 

二叉排序的查找

要在二叉树中找出查找最大最小元素是极简单的事情，从根节点一直往左走，直到无路可走就可得到最小值；从根节点一直往右走，直到无路可走，就可以得到最大值。

4.1 查找小元素

1 BSTNode* SearchMin(BSTNode* root)
2 {
3     if (root == NULL)
4         return NULL;
5     if (root->lchild == NULL)
6         return root;
7     else   
8         return SearchMin(root->lchild); //一直往左孩子找，直到没有左孩子的结点 
9 }

 

4.2 查找最大元素

1 BSTNode* SearchMin(BSTNode* root)
2 {
3     if (root == NULL)
4         return NULL;
5     if (root->rchild == NULL)
6         return root;
7     else   
8         return SearchMin(root->rchild); //一直往右孩子找，直到没有左孩子的结点 
9 }

 

4.3 查找某个元素

4.3.1 递归版

 1 BSTNode* SearchBSTNode(BSTNode* root, DataType key)
 2 {
 3     if (root == NULL)
 4         return NULL;
 5     if (key > root->data) //查找右子树  
 6         return SearchBSTNode(root->rchild, key);
 7     else if (key < root->data) //查找左子树  
 8         return SearchBSTNode(root->lchild, key);
 9     else
10         return root;
11 }

 

4.3.2非递归版

 1 BSTNode* Search_BST(BSTNode* root, DataType key)
 2 {
 3     BSTNode* p = root;
 4     while (p) 
 5     {       
 6         if (p->data == key)  return p;
 7         p = (key < p->data) ? p->lchild : p->rchild;
 8     }
 9     return NULL;
10 }

 

 

二叉排序的插入

5.1 代码

 1 bool InsertBST(BSTNode *&bt, char k)
 2 {
 3     if (bt == NULL)
 4     {
 5         bt = (BSTNode*)malloc(sizeof(BSTN);
 6         bt->key = k;
 7         bt->lchild = bt->rchild = NULL;
 8         return true;
 9     }
10     else if (k == bt->key)
11         return false;
12     else if (k < bt->key)
13         return InsertBST(bt->lchild, k);
14     else
15         return InsertBST(bt->rchild, k);
16 }

 

转载于:https://www.cnblogs.com/sunbines/p/9728040.html