P9117 [春季测试 2023] 涂色游戏 - 洛谷

原创已于 2025-07-26 00:07:17 修改 · 612 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2025-07-26 00:03:33 首次发布

c++ 洛谷oj正解专栏收录该内容

3 篇文章

订阅专栏

题目描述

有一天，小 D 在刷朋友圈时看到了一段游戏视频。

这个游戏的名字叫涂色游戏，视频中的游戏界面是一个 n 行 m 列的网格，初始时每一个格子都是白色（用数字 0 表示）。其中每一行的左侧、每一列的上方都有一把带颜色的刷子。玩家点击某个刷子后，这个刷子会将其右侧（或下方）的一整行（或一整列）涂上同一种颜色，该行（或该列）格子原有的颜色都会被覆盖成新涂上的颜色。

下图展示的情况可以通过先将第一列涂成红色，然后将第一行涂成蓝色得到，若此时选择将第三列涂成绿色，则图中绿色方框中的格子都会变成绿色。

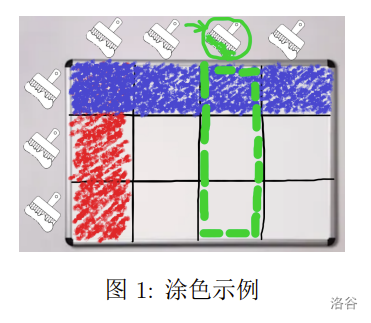
小 D 想用他自己编写的程序来进行视频中的游戏。在编程的过程中，小 D 在涂色逻辑的实现上却遇到了一些困难，于是他向你求助，希望你能帮他完成实现涂色逻辑部分的代码。

首先，小 D 会给你网格的行数和列数 n,m，然后给出 q 次操作，每次操作用三个整数 opti,xi,ci 表示：

如果 opti=0，那么这次操作会将第 xi 行涂成颜色 ci。
如果 opti=1，那么这次操作会将第 xi 列涂成颜色 ci。

在所有涂色操作结束以后，你需要输出网格中每个位置的颜色是什么。

输入格式

本题有多组测试数据。

第一行包含一个正整数 T，表示数据组数。

接下来一共 T 组数据，每组数据格式如下：

第一行包含三个整数 n,m,q，分别表示涂色板的行数、列数，以及小 D 进行涂色操作的次数。

接下来 q 行，每行包含三个整数 opti,xi,ci，表示一次操作。

输出格式

对于每组数据，输出 n 行，每行 m 个由单个空格隔开的整数。

其中第 i 行第 j 个整数表示涂色完成后网格中第 i 行第 j 列的方格是什么颜色。

输入输出样例

输入 #1复制

输出 #1复制

1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 1 1 0
1 1 1 1 1
3 2 2
3 0 0
3 1 1

我的思路

第1次思考

一开始我个人认为用一个较大的数组就可以模拟这个程序但事实告诉我：

----------------------------------(我是现实的分界线)------------------------------------------------------

1≤T≤10，1≤n,m≤105，0≤q≤105，0≤ci≤109。
若 opti=0，则 1≤xi≤n；若 opti=1，则 1≤xi≤m。
单个测试点中所有数据的 n⋅m 的总和不超过 106，q 的总和不超过 106。

测试点	n≤	m≤	q≤	性质 A	性质 B
1	1	1	0	√	√
2	1	1	1	√	√
3	1	10	20	√	√
4	1	105	105	×	√
5	1	105	105	×	√
6	1	105	105	×	×
7	10	10	20	√	√
8	50	50	100	√	√
9	50	50	100	√	×
10	1000	1000	2000	×	√
11	1000	1000	2000	×	×
12	1000	1000	2000	×	×
13	1000	1000	105	×	×
14	1000	1000	105	×	×
15	105	105	105	√	√
16	105	105	105	√	√
17	105	105	105	√	×
18	105	105	105	√	×
19	105	105	105	×	×
20	105	105	105	×	×

特殊性质 A：保证测试点中所有的 q⋅max(n,m) 之和不超过 107。

特殊性质 B：保证 opti=1。

----------------------------------------(我是up主的分界线)------------------------------------------

是的，数据量大的离谱

不管了，我们还是直接上暴力的代码吧:

Un AC code:

#include<iostream>
using namespace std;
int a[10010][10010];
void temp(){
	int m,n,q;
	cin>>n>>m>>q;
	for(int i = 1;i <= n;i++) {
		for(int j = 1;j <= m;j++) {
			a[i][j] = 0;
		}
	}
	while(q--){
		char op[2];
		cin>>op;
		int x,c;
		cin>>x>>c;
		if(op[0] == '0'){
			for(int i = 1;i <= n;i ++){
				a[x][i] = c;
			}
		}
		if(op[0] == '1'){
			for(int i = 1;i <= m;i ++) {
				a[i][x] = c;
			}
		}
	}
	for(int i = 1;i <= n;i ++) {
		for(int j = 1;j <= n;j ++){
			cout<<a[i][j]<<" ";
		}
		cout<<"\n";
	}
}
int main(){
	int t;
	cin>>t;
	while(t--){
		temp();
	}
}

结果也是理所当然的:

我的第2次思考

那么我们有没有一种方法可以让它降低时间复杂度并且不让他越界?

方法总比困难多，就算困难比方法多，我们也可以换个困难,所以我们这次不用二维数组了，

我们定义两个一维数组，一个代表横轴，一个代表数轴。

在输出的时候判断他这行是否被涂这样的话不仅可以不超界，还不会换得红色鲜艳的wa

那就让我们开始详细的说一下每个变量的分工吧：

ios::sync_with_stdio(false);
cin.tie(nullptr);

这个是对cin的加速 (说实话，cin比scanf慢)

用row_color表示横，用col_color表示纵轴。

特别特别注意

多测不清空，亲人两行泪

不要因为在归零的这个情况下，导致自己ac没了

说了这么久（久吗？)，相信你应该懂了。他其实就是个模拟，也不是特别的难。难就难在如何去，让它更快，我相信每个人都TLE过。

废话不多说，直接上ac代码：

#include <iostream>
using namespace std;

const int MAX_N = 100005; 
long long row_color[MAX_N], col_color[MAX_N]; 
long long row_time[MAX_N], col_time[MAX_N]; 

int main() {
    ios::sync_with_stdio(false); 
    cin.tie(nullptr);

    int T;
    cin >> T; 
    while (T--) {
        int n, m, q;
        cin >> n >> m >> q;

        fill(row_color, row_color + n + 1, 0);
        fill(col_color, col_color + m + 1, 0);
        fill(row_time, row_time + n + 1, 0);
        fill(col_time, col_time + m + 1, 0);

        for (int i = 1; i <= q; i++) {
            int opt, x;
            long long c;
            cin >> opt >> x >> c;
            if (opt == 0) { 
                row_color[x] = c;
                row_time[x] = i; 
            }
            else {
                col_color[x] = c;
                col_time[x] = i; 
            }
        }

       
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (row_time[i] > col_time[j]) {
                    cout << row_color[i]; 
                }
                else {
                    cout << col_color[j]; 
                }
                if (j < m) cout << " ";
            }
            cout << "\n";
        }
    }
    return 0;
}