P1983 [NOIP 2013 普及组] 车站分级 -洛谷正解

原创于 2025-07-15 21:02:37 发布 · 334 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#算法

c++ 洛谷oj正解专栏收录该内容

3 篇文章

订阅专栏

题目描述

一条单向的铁路线上，依次有编号为 1,2,…,n 的 n 个火车站。每个火车站都有一个级别，最低为 1 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。
注意：起始站和终点站自然也算作事先已知需要停靠的站点。

例如，下表是 5 趟车次的运行情况。其中，前 4 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（2 级）却未停靠途经的 6 号火车站（亦为 2 级）而不满足要求。

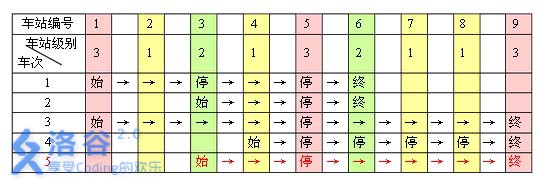
现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的级别。

输入格式

第一行包含 2 个正整数 n,m，用一个空格隔开。

第 i+1 行 (1≤i≤m) 中，首先是一个正整数 si (2≤si≤n)，表示第 i 趟车次有 si 个停靠站；接下来有 si 个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式

一个正整数，即 n 个火车站最少划分的级别数。

输入输出样例

输入 #1复制运行

9 2 
4 1 3 5 6 
3 3 5 6

输出 #1复制运行

输入 #2复制运行

输出 #2复制运行

说明/提示

对于 20% 的数据，1≤n,m≤10；

对于 50% 的数据，1≤n,m≤100；

对于 100% 的数据，1≤n,m≤1000

正解：

1.理解题意

首先我们知道对于每一列车它经过的站点中停了的站点的等级肯定比没停的站点高。因此对于每一辆车，我们可以把它经过的每一个没停的站点向每个停了的站点建在一条边，然后我们就可以得到一条队列，在这条队列上找到最长的一条路段即可。

然后我们就建立了两车之间的大小关系。

但是还有一点要注意，因为我们处理的是车，而最后要求的是点，如果对于一辆等级为一的车，他经过的站点中如果有一个站点，一辆车都没停靠，那么最后的答案就要加一。增加一辆每个站都停的列车来作为等级最低的列车，因为经过我们前面可以求出所有列车的等级，但是里面等级最低的一个车要是有一个站没停，就存在着更低的一辆车，这样才是正确的把点的等级转化为站的等级。

最终代码：

#include<iostream>
using namespace std;
struct cs {             //链式前向星存图a:存储边信息,to：指向的目标节点,next：指向上一条边的编号。
    int to, next;
} a[1000001];
int b[1001], f[1001], head[1001];     //b[]：暂存一趟车次的停靠站编号,f[]：记录每个节点的最长路径长度,head[]：链式前向星的头节点数组,vi[][]：防止重边（记录是否添加过边）,n：车站数量,m：车次数量,ll：边的总数。ans：答案，最长路径长度
bool vi[1001][1001];
int n, m, x, y, z, ans = 0, ll;
void init(int x, int y) {       //添加一条从 x 到 y 的边。
    a[++ll].to = y;
    a[ll].next = head[x];
    head[x] = ll;
}
int dfs(int x) {            //求以 x 为起点的最长路径长度(回溯，深搜）
    for (int k = head[x]; k; k = a[k].next)
        if (!f[a[k].to])
            f[x] = max(f[x], dfs(a[k].to));
        else
            f[x] = max(f[x], f[a[k].to]);
    return ++f[x];
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        cin >> z;
        for (int i = 1; i <= z; i++) cin >> b[i];
        int l = 1;
        for (int i = b[1]; i < b[z]; i++) {
            if (b[l] == i) {
                l++;
                continue;
            }
            else {
                for (int k = 1; k <= z; k++) {
                    if (!vi[b[k]][i]) {
                        init(b[k], i);
                        vi[b[k]][i] = 1;
                    }
                }
            }
        }
    }
    for (int i = 1; i <= n; i++) {
        if (!f[i]) {
            ans = max(ans, dfs(i));     //遍历所有节点，未访问过的节点从 dfs(i) 开始,ans 记录所有 dfs(i) 的最大值，即为最小划分的级别数
        }
    }
    cout << ans;
    return 0;
}