Transformer Language Model Architecture
零、 环境设置
我们每次都去激活环境太繁琐这里建议直接把激活环境的命令写进.bashrc文件
找到家目录下的.bashrc文件
然后找到项目根目录下面有一个.venv文件

.venv目录下有一个bin,然后bin中有一个activate脚本,这个脚本就是用来激活uv环境的,我们只需要在每次打开终端也就是shell启动的时候执行一遍这个脚本就好了。

其实就是在.bashrc文件中加上一句source命令
source /root/css336/.venv/bin/activate # 这个路径文件需要和自己uv环境所在路径对应
一、 Basic Building Blocks: Linear and Embedding Modules
Parameter Initialization 初始化参数
根据之前深度学习基础,模型参数的初始化对于模型训练是很重要的,参数初始化的不好会引起梯度消失或梯度爆炸。
这里初始化采用截断高斯分布,来避免参数值过大或过小。
线性层(Linear weights):
N
(
μ
=
0
,
σ
=
2
d
i
n
+
d
o
u
t
)
\mathcal{N}(\mu=0, \sigma=\frac{2}{d_{in} + d_{out}})
N(μ=0,σ=din+dout2) 截断
[
−
3
σ
,
+
3
σ
]
[-3\sigma,+3\sigma]
[−3σ,+3σ]
嵌入层(embedding):
N
(
μ
=
0
,
σ
=
1
)
\mathcal{N}(\mu=0, \sigma=1)
N(μ=0,σ=1) 截断
[
−
3
,
+
3
]
[-3,+3]
[−3,+3]
具体的实现是使用pytorch中的torch.nn.init.trunc_normal。torch.nn.init.trunc_normal会从正态分布中采样,如果采样得到的结果落在截断范围外则丢弃重新进行采样,直到所有值均落在截断范围内。
就比如上面嵌入层embedding的初始化
torch.nn.init.trunc_normal_(
tensor,
mean=0.0,
std=1.0,
a=-3.0,
b=3.0
)
| 参数 | 类型 | 默认值 | 说明 |
|---|---|---|---|
| tensor | Tensor | — | 要初始化的张量(in-place 操作) |
| mean | float | 0.0 | 正态分布的均值 |
| std | float | 1.0 | 正态分布的标准差 |
| a | float | -3.0 | 截断下界(以标准差为单位) |
| b | float | 3.0 | 截断上界(以标准差为单位) |
Linear Module 线性模块
import torch
from torch import nn
from torch.nn.init import trunc_normal_
from einops import einsum
class Linear(nn.Module):
def __init__(
self,
in_features: int,
out_features: int,
device = None,
dtype = None):
super().__init__()
self.in_features = in_features
self.out_features = out_features
factory_kwargs = {'device': device, 'dtype': dtype}
self.W = nn.Parameter(torch.empty(out_features, in_features, **factory_kwargs))
std = (2 / (in_features + out_features)) ** 0.5
trunc_normal_(self.W, mean=0.0, std=std, a=-3.0*std, b=3.0*std)
def forward(self, x: torch.Tensor) -> torch.Tensor:
return einsum(x, self.W, '... in, out in -> ... out')
编写adapter.py进行测试
import layer
def run_linear(
d_in: int,
d_out: int,
weights: Float[Tensor, " d_out d_in"],
in_features: Float[Tensor, " ... d_in"],
) -> Float[Tensor, " ... d_out"]:
"""
Given the weights of a Linear layer, compute the transformation of a batched input.
Args:
in_dim (int): The size of the input dimension
out_dim (int): The size of the output dimension
weights (Float[Tensor, "d_out d_in"]): The linear weights to use
in_features (Float[Tensor, "... d_in"]): The output tensor to apply the function to
Returns:
Float[Tensor, "... d_out"]: The transformed output of your linear module.
"""
device, dtype = in_features.device, in_features.dtype
model = layer.Linear(d_in, d_out, device, dtype)
model.load_state_dict({'W': weights})
return model.forward(in_features)
进入test目录中然后执行
pytest test_model.py::test_linear
在进行执行前
测试通过后会显示下面的结果。

这里面涉及一些einops和nn.Parameter的用法。
Embedding module
embdding的初始化也是使用torch.nn.init.trunc_normal函数
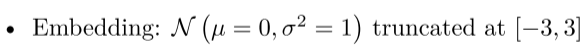
class Embedding(nn.Module):
def __init__(
self,
num_embeddings: int,
embedding_dim: int,
device: torch.device | None = None,
dtype: torch.dtype | None = None
):
super().__init__()
self.num_embeddings = num_embeddings
self.embedding_dim = embedding_dim
factory_kwargs = {'device': device, 'dtype': dtype}
self.W = nn.Parameter(torch.empty(num_embeddings, embedding_dim, **factory_kwargs))
std = 1
trunc_normal_(self.W, mean=0.0, std=std, a=-3.0*std, b=3.0*std)
def forward(self, token_ids: torch.Tensor) -> torch.Tensor:
return self.W[token_ids]
编写测试adapter
def run_embedding(
vocab_size: int,
d_model: int,
weights: Float[Tensor, " vocab_size d_model"],
token_ids: Int[Tensor, " ..."],
) -> Float[Tensor, " ... d_model"]:
"""
Given the weights of an Embedding layer, get the embeddings for a batch of token ids.
Args:
vocab_size (int): The number of embeddings in the vocabulary
d_model (int): The size of the embedding dimension
weights (Float[Tensor, "vocab_size d_model"]): The embedding vectors to fetch from
token_ids (Int[Tensor, "..."]): The set of token ids to fetch from the Embedding layer
Returns:
Float[Tensor, "... d_model"]: Batch of embeddings returned by your Embedding layer.
"""
device, dtype = weights.device, weights.dtype
model = layer.Embedding(vocab_size, d_model, device, dtype)
model.load_state_dict({'W': weights})
return model.forward(token_ids)
测试
pytest test_model.py::test_embedding
测试通过后会显示下面的结果。
二、 Pre-Norm Transformer Block
Root Mean Square Layer Normalization
我们要实现的transformer和原论文中的transformer的结构并不相同,就比如normliaztion,这里使用的是pre-norm,pre-norm被认为能改善梯度流(因为原始的数据是没有经过任何处理直接通过residual加到最后的结果)具体参考Stanford CS336 Lecture3 | Architectures, hyperparameters。
关于RMSNorm的原理

a
i
a_i
ai为一个
(
d
m
o
d
e
l
,
)
(d_{model}, )
(dmodel,)维的activation,g是可学习的增益参数。
class RMSNorm(nn.Module):
def __init__(
self,
d_model: int,
eps: float = 1e-5,
device: torch.device | None = None,
dtype: torch.dtype | None = None):
super().__init__()
self.d_model = d_model
self.eps = eps
factory_kwargs = {'device': device, 'dtype': dtype}
self.W = nn.Parameter(torch.ones(d_model, **factory_kwargs))
def forward(self, x: torch.Tensor) -> torch.Tensor:
in_dtype = x.dtype
x = x.to(torch.float32)
RMS = (x.pow(2).mean(dim=-1, keepdim=True) + self.eps).sqrt()
x /= RMS
x *= self.W
return x.to(in_dtype)
adapters
def run_rmsnorm(
d_model: int,
eps: float,
weights: Float[Tensor, " d_model"],
in_features: Float[Tensor, " ... d_model"],
) -> Float[Tensor, " ... d_model"]:
"""Given the weights of a RMSNorm affine transform,
return the output of running RMSNorm on the input features.
Args:
d_model (int): The dimensionality of the RMSNorm input.
eps: (float): A value added to the denominator for numerical stability.
weights (Float[Tensor, "d_model"]): RMSNorm weights.
in_features (Float[Tensor, "... d_model"]): Input features to run RMSNorm on. Can have arbitrary leading
dimensions.
Returns:
Float[Tensor,"... d_model"]: Tensor of with the same shape as `in_features` with the output of running
RMSNorm of the `in_features`.
"""
device, dtype = weights.device, weights.dtype
model = layer.RMSNorm(d_model, eps, device, dtype)
model.load_state_dict({'W': weights})
return model.forward(in_features)
测试
pytest test_model.py::test_rmsnorm

Position-Wise Feed-Forward Network
这里实现的是经过改进的FFN,加入了门控,同时激活函数使用SiLU 或者Swish。

上面都是列向量表示,因为在pytorch中是行优先存储的原则,所以这里需要对上面的公式进行相关修改
G
L
U
(
x
,
W
1
,
W
2
)
=
σ
(
x
W
1
T
)
⊙
(
x
W
2
T
)
GLU(x, W_1, W_2)=\sigma(xW_1^T) \odot (xW_2^T)
GLU(x,W1,W2)=σ(xW1T)⊙(xW2T)
F
F
N
(
x
)
=
S
w
i
G
L
U
(
x
,
W
1
,
W
2
,
W
3
)
=
(
S
i
L
U
(
x
W
1
T
)
⊙
(
x
W
3
T
)
)
W
2
T
FFN(x)=SwiGLU(x,W_1,W_2,W_3)=(SiLU(xW_1^T) \odot (xW_3^T))W_2^T
FFN(x)=SwiGLU(x,W1,W2,W3)=(SiLU(xW1T)⊙(xW3T))W2T
同时
d
f
f
=
8
3
d
m
o
d
e
l
d_{ff}=\frac{8}{3} d_{model}
dff=38dmodel,这个原因主要是为了保持参数量一致和原FFN,具体可以参考Stanford CS336 Lecture3 | Architectures, hyperparameters或者lecture 3的视频和ppt中均有解释。
实现如下:assignment1的pdf中有说可以使用torch.sigmoid,这里直接使用了没有自己手动实现sigmoid函数。
def SiLU(x: torch.Tensor) -> torch.Tensor:
return x * torch.sigmoid(x)
class SwiGLU(nn.Module):
def __init__(
self,
d_model: int,
d_ff: int,
device: torch.device | None = None,
dtype: torch.dtype | None = None
):
super().__init__()
self.d_model = d_model
self.d_ff = d_ff
factory_kwargs = {'device': device, 'dtype': dtype}
self.linear1 = Linear(d_model, d_ff)
self.linear2 = Linear(d_ff, d_model)
self.linear3 = Linear(d_model, d_ff)
def forward(self, x: Float[torch.Tensor, "... d_model"]) -> Float[torch.Tensor, "... d_model"]:
xW1 = self.linear1(x)
xW3 = self.linear3(x)
return self.linear2(SiLU(xW1) * xW3)
adapters中
def run_swiglu(
d_model: int,
d_ff: int,
w1_weight: Float[Tensor, " d_ff d_model"],
w2_weight: Float[Tensor, " d_model d_ff"],
w3_weight: Float[Tensor, " d_ff d_model"],
in_features: Float[Tensor, " ... d_model"],
) -> Float[Tensor, " ... d_model"]:
"""Given the weights of a SwiGLU network, return
the output of your implementation with these weights.
Args:
d_model (int): Dimensionality of the feedforward input and output.
d_ff (int): Dimensionality of the up-project happening internally to your swiglu.
w1_weight (Float[Tensor, "d_ff d_model"]): Stored weights for W1
w2_weight (Float[Tensor, "d_model d_ff"]): Stored weights for W2
w3_weight (Float[Tensor, "d_ff d_model"]): Stored weights for W3
in_features (Float[Tensor, "... d_model"]): Input embeddings to the feed-forward layer.
Returns:
Float[Tensor, "... d_model"]: Output embeddings of the same shape as the input embeddings.
"""
# Example:
# If your state dict keys match, you can use `load_state_dict()`
# swiglu.load_state_dict(weights)
# You can also manually assign the weights
# swiglu.w1.weight.data = w1_weight
# swiglu.w2.weight.data = w2_weight
# swiglu.w3.weight.data = w3_weight
device, dtype = w1_weight.device, w1_weight.dtype
model = layer.SwiGLU(d_model, d_ff, device, dtype)
model.load_state_dict({
"linear1.W": w1_weight,
"linear2.W": w2_weight,
"linear3.W": w3_weight,
})
return model.forward(in_features)
测试命令
pytest test_model.py::test_swiglu

还需要测试一下SiLU
pytest test_model.py::test_silu_matches_pytorch

Relative Positional Embeddings
数学上实现RoPE是通过旋转矩阵,对于给定的一个query token
q
(
i
)
=
W
q
x
(
i
)
∈
R
d
q^{(i)} = W_qx^{(i)} \in \mathbb{R}^d
q(i)=Wqx(i)∈Rd,query token的位置为i,可以使用成对的旋转矩阵(偶数)
R
i
R^i
Ri 给query token加入位置信息后
q
′
(
i
)
=
R
i
q
(
i
)
=
R
i
W
q
x
(
i
)
q^{'(i)}=R^iq^{(i)}=R^i W_qx^{(i)}
q′(i)=Riq(i)=RiWqx(i)
这里,
R
i
R_i
Ri会将嵌入向量中每一对元素
q
(
i
)
2
k
:
2
k
+
1
q(i)_{2k:2k+1}
q(i)2k:2k+1视为一个二维向量,并将其旋转一个角度
θ
i
,
k
=
i
Θ
2
k
/
d
\theta_{i,k}=\frac{i}{\Theta^{2k/d}}
θi,k=Θ2k/di,其中
k
=
{
0
,
1
,
2
,
d
/
2
}
k=\{0, 1, 2,d/2\}
k={0,1,2,d/2},而
Θ
\Theta
Θ是一个常数,通常取1000,可以将整个旋转矩阵视为一个分块对角矩阵,其对角线上包含
d
2
个
2
×
2
\frac{d}{2}个 2 \times 2
2d个2×2旋转块
R
i
,
k
R_{i,k}
Ri,k
R
k
i
=
[
c
o
s
(
θ
i
,
k
)
−
s
i
n
(
θ
i
,
k
)
s
i
n
(
θ
i
,
k
)
c
o
s
(
θ
i
,
k
)
]
R_k^i=\begin{bmatrix} cos(\theta_{i, k})& -sin(\theta_{i, k})\\ sin(\theta_{i, k}) & cos(\theta_{i, k}) \end{bmatrix}
Rki=[cos(θi,k)sin(θi,k)−sin(θi,k)cos(θi,k)]
R
i
=
[
R
1
i
0
0
⋯
0
0
R
2
i
0
⋯
0
0
0
R
3
i
⋯
0
⋮
⋮
⋮
⋱
⋮
0
0
0
⋯
R
d
/
2
i
]
R^i = \begin{bmatrix} R_1^i & 0 & 0 & \cdots & 0 \\ 0 & R_2^i & 0 & \cdots & 0 \\ 0 & 0 & R_3^i & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & R_{d/2}^i \end{bmatrix}
Ri=
R1i00⋮00R2i0⋮000R3i⋮0⋯⋯⋯⋱⋯000⋮Rd/2i
上面是RoPE的数学原理,但是实际上实现RoPE时,并不会显示构造旋转矩阵,因为这样效率比较低,通常是构造cos、sin矩阵然后再分奇偶应用,具体操作如下:
先根据
θ
i
,
k
=
i
Θ
2
k
/
d
\theta_{i,k}=\frac{i}{\Theta^{2k/d}}
θi,k=Θ2k/di,其中
k
=
{
0
,
1
,
2
,
d
/
2
}
k=\{0, 1, 2,d/2\}
k={0,1,2,d/2} 构造
θ
i
,
k
\theta_{i,k}
θi,k矩阵,这里可以使用torch.arange生成关于
1
Θ
2
k
/
d
\frac{1}{\Theta^{2k/d}}
Θ2k/d1的向量
freq = 1.0 / (theta ** (torch.arange(0, d - 1, 2) / d))
然后使用torch.outer,对每个位置和freq做外积得到矩阵
positions = torch.arange(0, max_seq_len, device=device).float()
freqs = torch.outer(positions, freq)
我们可以先忽略批次操作因为前面的维度不会对计算产生影响
下面构造sin、cos矩阵
self.register_buffer('cos_cache', torch.cos(torch.tensor(freqs)))
self.register_buffer('sin_cache', torch.sin(torch.tensor(freqs)))
假设对于第i个token只有两维,即
d
m
o
d
e
l
=
2
d_{model}=2
dmodel=2
[
x
0
,
x
1
]
×
[
c
o
s
(
θ
i
,
0
)
−
s
i
n
(
θ
i
,
0
)
s
i
n
(
θ
i
,
0
)
c
o
s
(
θ
i
,
0
)
]
=
[
x
0
c
o
s
+
x
1
s
i
n
,
−
x
0
s
i
n
+
x
1
c
o
s
]
\begin{bmatrix}x_0, x_1\end{bmatrix} \times \begin{bmatrix} cos(\theta_{i, 0})& -sin(\theta_{i, 0})\\ sin(\theta_{i, 0}) & cos(\theta_{i, 0}) \end{bmatrix}=\begin{bmatrix}x_0cos + x_1sin, -x_0sin+x_1cos\end{bmatrix}
[x0,x1]×[cos(θi,0)sin(θi,0)−sin(θi,0)cos(θi,0)]=[x0cos+x1sin,−x0sin+x1cos]
[
x
2
,
x
3
]
×
[
c
o
s
(
θ
i
,
1
)
−
s
i
n
(
θ
i
,
1
)
s
i
n
(
θ
i
,
1
)
c
o
s
(
θ
i
,
1
)
]
=
[
x
2
c
o
s
+
x
3
s
i
n
,
−
x
2
s
i
n
+
x
3
c
o
s
]
\begin{bmatrix}x_2, x_3\end{bmatrix} \times \begin{bmatrix} cos(\theta_{i, 1})& -sin(\theta_{i, 1})\\ sin(\theta_{i, 1}) & cos(\theta_{i, 1}) \end{bmatrix}=\begin{bmatrix}x_2cos + x_3sin, -x_2sin+x_3cos\end{bmatrix}
[x2,x3]×[cos(θi,1)sin(θi,1)−sin(θi,1)cos(θi,1)]=[x2cos+x3sin,−x2sin+x3cos]
如果我们单独把偶数、奇数拿出来,然后再还原回去就对token i完成了处理。
也就是
[
x
0
,
x
2
,
x
4
,
.
.
.
x
d
/
2
]
⊗
[
c
o
s
(
θ
i
,
0
)
,
c
o
s
(
θ
i
,
1
)
,
c
o
s
(
θ
i
,
2
)
,
.
.
.
.
c
o
s
(
θ
i
,
d
/
2
)
]
+
[
x
1
,
x
3
,
x
5
,
.
.
.
x
d
/
2
−
1
]
⊗
[
s
i
n
(
θ
i
,
0
)
,
s
i
n
(
θ
i
,
1
)
,
s
i
n
(
θ
i
,
2
)
,
.
.
.
.
s
i
n
(
θ
i
,
d
/
2
)
]
[x_0, x_2, x_4,...x_{d/2}] \otimes [cos(\theta_{i,0}),cos(\theta_{i,1}),cos(\theta_{i,2}),....cos(\theta_{i,d/2})] + [x_1, x_3, x_5,...x_{d/2-1} ]\otimes [sin(\theta_{i,0}),sin(\theta_{i,1}),sin(\theta_{i,2}),....sin(\theta_{i,d/2})]
[x0,x2,x4,...xd/2]⊗[cos(θi,0),cos(θi,1),cos(θi,2),....cos(θi,d/2)]+[x1,x3,x5,...xd/2−1]⊗[sin(θi,0),sin(θi,1),sin(θi,2),....sin(θi,d/2)]即为结果的偶数项
[ x 0 , x 2 , x 4 , . . . x d / 2 ] ⊗ − [ s i n ( θ i , 0 ) , s i n ( θ i , 1 ) , s i n ( θ i , 2 ) , . . . . s i n ( θ i , d / 2 ) ] + [ x 1 , x 3 , x 5 , . . . x d / 2 − 1 ] ⊗ [ c o s ( θ i , 0 ) , c o s ( θ i , 1 ) , c o s ( θ i , 2 ) , . . . . c o s ( θ i , d / 2 ) ] [x_0, x_2, x_4,...x_{d/2}] \otimes - [sin(\theta_{i,0}),sin(\theta_{i,1}),sin(\theta_{i,2}),....sin(\theta_{i,d/2})] + [x_1, x_3, x_5,...x_{d/2-1} ]\otimes [cos(\theta_{i,0}),cos(\theta_{i,1}),cos(\theta_{i,2}),....cos(\theta_{i,d/2})] [x0,x2,x4,...xd/2]⊗−[sin(θi,0),sin(θi,1),sin(θi,2),....sin(θi,d/2)]+[x1,x3,x5,...xd/2−1]⊗[cos(θi,0),cos(θi,1),cos(θi,2),....cos(θi,d/2)]为结果的奇数项
于是就可以按上述方法实现。
class RotaryPositionalEmbedding(nn.Module):
def __init__(
self,
theta: float,
d_k: int,
max_seq_len: int,
device = None
):
super().__init__()
self.theta = theta
assert d_k % 2 == 0, 'd_k is not even'
self.d_k = d_k
self.max_seq_len = max_seq_len
factory_kwargs = {'device': device}
freq = 1.0 / (theta ** (torch.arange(0, d_k, 2, device=device).float() / d_k))
positions = torch.arange(0, max_seq_len, device=device).float()
freqs = torch.outer(positions, freq)
self.register_buffer('cos_cache', torch.cos(torch.tensor(freqs)))
self.register_buffer('sin_cache', torch.sin(torch.tensor(freqs)))
def forward(
self,
x: Float[torch.Tensor, "... seq_len d_k"],
token_positions: Int[torch.Tensor, "... seq_len"]
) -> Float[torch.Tensor, "... seq_len d_k"]:
sin = self.sin_cache[token_positions]
cos = self.cos_cache[token_positions]
x_even = x[..., ::2]
x_odd = x[..., 1::2]
out_even = x_even * cos - x_odd * sin
out_odd = x_even * sin + x_odd * cos
out = torch.empty_like(x)
out[..., ::2] = out_even
out[..., 1::2] = out_odd
return out
这里面还有一些内容如register_buffer的使用,以及pytorch的广播机制、二维tensor也可以作为索引的内容需要去补充、以及torch.empty_like的用法
adapters的编写
def run_rope(
d_k: int,
theta: float,
max_seq_len: int,
in_query_or_key: Float[Tensor, " ... sequence_length d_k"],
token_positions: Int[Tensor, " ... sequence_length"],
) -> Float[Tensor, " ... sequence_length d_k"]:
"""
Run RoPE for a given input tensor.
Args:
d_k (int): Embedding dimension size for the query or key tensor.
theta (float): RoPE parameter.
max_seq_len (int): Maximum sequence length to pre-cache if your implementation does that.
in_query_or_key (Float[Tensor, "... sequence_length d_k"]): Input tensor to run RoPE on.
token_positions (Int[Tensor, "... sequence_length"]): Tensor of shape (batch_size, sequence_length) with the token positions
Returns:
Float[Tensor, " ... sequence_length d_k"]: Tensor with RoPEd input.
"""
device = in_query_or_key.device
model = layer.RotaryPositionalEmbedding(theta, d_k, max_seq_len, device)
return model.forward(in_query_or_key, token_positions)
运行测试脚本
pytest test_model.py::test_rope
测试结果如下图:

Scaled Dot-Product Attention
首先需要实现softmax函数,这里面有一个放置数值溢出的方法
我们知道
e
x
e^x
ex当x稍微大一些就会导致
e
x
e^x
ex变得巨大,从而inf,于是inf / inf就会出现Nan,导致后面没办法计算,于是我们选择将所有数都减去这些数中的最大值,于是都变为<=0的数,就可以避免上述问题。
def softmax(x: torch.Tensor, dim: int) -> torch.Tensor:
x_max = x.max(dim=dim, keepdim=True).values
exp_x = torch.exp(x - x_max)
return exp_x / exp_x.sum(dim=dim, keepdim=True)
修改adapters
def run_softmax(in_features: Float[Tensor, " ..."], dim: int) -> Float[Tensor, " ..."]:
"""
Given a tensor of inputs, return the output of softmaxing the given `dim`
of the input.
Args:
in_features (Float[Tensor, "..."]): Input features to softmax. Shape is arbitrary.
dim (int): Dimension of the `in_features` to apply softmax to.
Returns:
Float[Tensor, "..."]: Tensor of with the same shape as `in_features` with the output of
softmax normalizing the specified `dim`.
"""
return layer.softmax(in_features, dim)
测试
pytest -k test_softmax_matches_pytorch

下面就是实现缩放点积注意力机制了
按照pdf中的公式也就是《attention is all you need》论文中的去实现就好了,注意我们使用的是行向量去实现的,这个公式里面是列向量

class ScaledDotProductAttention(nn.Module):
def __init__(
self,
d_k: int
):
super().__init__()
self.scale = 1.0 / math.sqrt(d_k)
def forward(
self,
q: Float[torch.Tensor, "... seq_len_q d_k"],
k: Float[torch.Tensor, "... seq_len_k d_k"],
v: Float[torch.Tensor, "... seq_len_k d_v"],
mask: Bool[torch.Tensor, "seq_len_q seq_len_k"] | None = None
) -> Float[torch.Tensor, "... seq_len_q d_v"]:
attention_score = einsum(q, k, "... seq_len_q d_k, ... seq_len_k d_k -> ... seq_len_q seq_len_k") * self.scale
if mask is not None:
attention_score = attention_score.masked_fill(~mask, float("-inf"))
attention_score = softmax(attention_score, dim=-1)
return einsum(attention_score, v, "... seq_len_q seq_len_k, ... seq_len_k d_v -> ... seq_len_q d_v")
这里有个bug我d了10分钟,就是
tensor.masked_fill不是原地操作的,他的原地版本是tensor.masked_fill_,使用非原地操作的需要再赋一次值。
在adapters中调用
def run_scaled_dot_product_attention(
Q: Float[Tensor, " ... queries d_k"],
K: Float[Tensor, " ... keys d_k"],
V: Float[Tensor, " ... values d_v"],
mask: Float[Tensor, " ... queries keys"] | None = None,
) -> Float[Tensor, " ... queries d_v"]:
"""
Given key (K), query (Q), and value (V) tensors, return
the output of your scaled dot product attention implementation.
Args:
Q (Float[Tensor, " ... queries d_k"]): Query tensor
K (Float[Tensor, " ... keys d_k"]): Key tensor
V (Float[Tensor, " ... values d_v"]): Values tensor
mask (Float[Tensor, " ... queries keys"] | None): Mask tensor
Returns:
Float[Tensor, " ... queries d_v"]: Output of SDPA
"""
model = layer.ScaledDotProductAttention(d_k=Q.shape[-1])
return model(Q, K, V, mask=mask)
测试
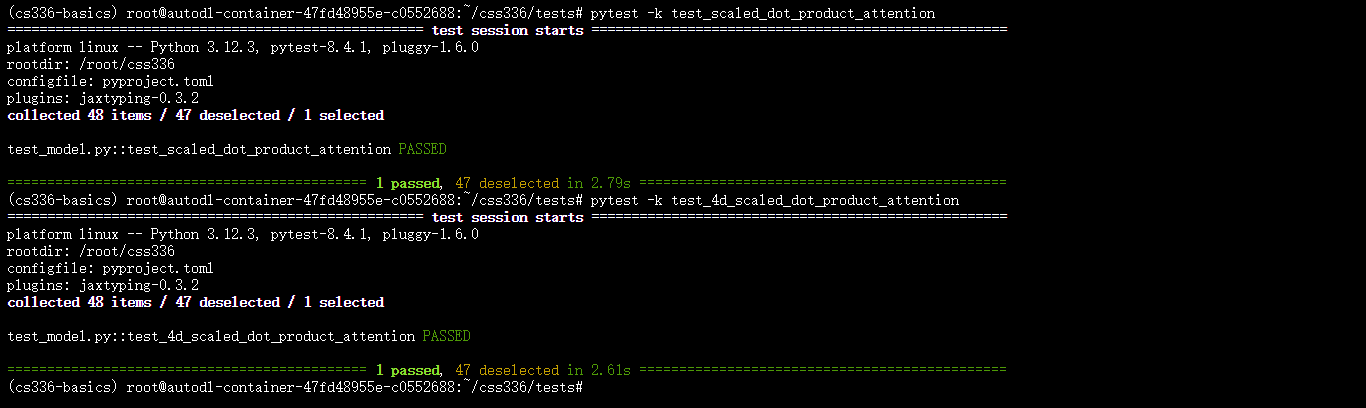
pytest -k test_scaled_dot_product_attention
pytest -k test_4d_scaled_dot_product_attention
Causal Multi-Head Self-Attention

多头自注意力的实现是建立在前面点积注意力的基础上,这里新引入了4个线性层对模型进行线性变换,实现起来不难,但是有很多小细节。
class CausalMultiheadSelfAttention(nn.Module):
def __init__(
self,
d_model: int,
num_heads: int,
max_seq_len: int | None = None,
theta: float = 10000.0,
use_rope: bool = True,
device: torch.device | None = None,
dtype: torch.dtype | None = None
):
super().__init__()
assert d_model % num_heads == 0, "d_model can not divide num_heads"
factory_kwargs = {'device': device, 'dtype': dtype}
mask = torch.tril(torch.ones(max_seq_len, max_seq_len, dtype=torch.bool, device=device))
self.mask = mask.unsqueeze(0).unsqueeze(0)
self.d_model = d_model
self.num_heads = num_heads
self.max_seq_len = max_seq_len
self.theta = theta
self.use_rope = use_rope
self.d_k = d_model // num_heads
self.d_v = self.d_k
self.attn = ScaledDotProductAttention(self.d_k)
self.q_proj, self.k_proj, self.v_proj, self.o_proj = [Linear(d_model, d_model, **factory_kwargs) for i in range(4)]
if use_rope is True:
self.rope = RotaryPositionalEmbedding(
theta=theta,
d_k=self.d_k,
max_seq_len=max_seq_len,
device=device
)
def forward(
self,
x: Float[torch.Tensor, "batch_size seq_len d_model"],
token_positions: Int[torch.Tensor, " batch_size sequence_length"] | None = None,
) -> Float[torch.Tensor, "batch_size seq_len d_model"]:
B, S, _ = x.shape
q, k, v = [rearrange(proj(x), 'b s (h d) -> b h s d', h = self.num_heads) for proj in [self.q_proj, self.k_proj, self.v_proj]]
if self.use_rope is True:
q, k = self.rope(q, token_positions), self.rope(k, token_positions)
out = self.attn(q, k, v, self.mask[..., :S, :S])
return self.o_proj(rearrange(out, 'b h s d -> b s (h d)'))
adapters,如果只是结果不对看看是不是忘记加载Wq, Wk, Wv, Wo这四个模型参数了
def run_multihead_self_attention(
d_model: int,
num_heads: int,
q_proj_weight: Float[Tensor, " d_k d_in"],
k_proj_weight: Float[Tensor, " d_k d_in"],
v_proj_weight: Float[Tensor, " d_v d_in"],
o_proj_weight: Float[Tensor, " d_model d_v"],
in_features: Float[Tensor, " ... sequence_length d_in"],
) -> Float[Tensor, " ... sequence_length d_out"]:
"""
Given the key, query, and value projection weights of a naive unbatched
implementation of multi-head attention, return the output of an optimized batched
implementation. This implementation should handle the key, query, and value projections
for all heads in a single matrix multiply.
This function should not use RoPE.
See section 3.2.2 of Vaswani et al., 2017.
Args:
d_model (int): Dimensionality of the feedforward input and output.
num_heads (int): Number of heads to use in multi-headed attention.
max_seq_len (int): Maximum sequence length to pre-cache if your implementation does that.
q_proj_weight (Float[Tensor, "d_k d_in"]): Weights for the Q projection
k_proj_weight (Float[Tensor, "d_k d_in"]): Weights for the K projection
v_proj_weight (Float[Tensor, "d_k d_in"]): Weights for the V projection
o_proj_weight (Float[Tensor, "d_model d_v"]): Weights for the output projection
in_features (Float[Tensor, "... sequence_length d_in"]): Tensor to run your implementation on.
Returns:
Float[Tensor, " ... sequence_length d_out"]: Tensor with the output of running your optimized, batched multi-headed attention
implementation with the given QKV projection weights and input features.
"""
device, dtype = in_features.device, in_features.dtype
model = layer.CausalMultiheadSelfAttention(
d_model=d_model,
num_heads=num_heads,
max_seq_len = in_features.size(-2),
use_rope=False,
device=device,
dtype=dtype
)
model.load_state_dict({
"q_proj.W": q_proj_weight,
"k_proj.W": k_proj_weight,
"v_proj.W": v_proj_weight,
"o_proj.W": o_proj_weight,
}, strict=False)
return model(in_features)
def run_multihead_self_attention_with_rope(
d_model: int,
num_heads: int,
max_seq_len: int,
theta: float,
q_proj_weight: Float[Tensor, " d_k d_in"],
k_proj_weight: Float[Tensor, " d_k d_in"],
v_proj_weight: Float[Tensor, " d_v d_in"],
o_proj_weight: Float[Tensor, " d_model d_v"],
in_features: Float[Tensor, " ... sequence_length d_in"],
token_positions: Int[Tensor, " ... sequence_length"] | None = None,
) -> Float[Tensor, " ... sequence_length d_out"]:
"""
Given the key, query, and value projection weights of a naive unbatched
implementation of multi-head attention, return the output of an optimized batched
implementation. This implementation should handle the key, query, and value projections
for all heads in a single matrix multiply.
This version of MHA should include RoPE.
In this case, the RoPE embedding dimension must be the head embedding dimension (d_model // num_heads).
See section 3.2.2 of Vaswani et al., 2017.
Args:
d_model (int): Dimensionality of the feedforward input and output.
num_heads (int): Number of heads to use in multi-headed attention.
max_seq_len (int): Maximum sequence length to pre-cache if your implementation does that.
theta (float): RoPE parameter.
q_proj_weight (Float[Tensor, "d_k d_in"]): Weights for the Q projection
k_proj_weight (Float[Tensor, "d_k d_in"]): Weights for the K projection
v_proj_weight (Float[Tensor, "d_k d_in"]): Weights for the V projection
o_proj_weight (Float[Tensor, "d_model d_v"]): Weights for the output projection
in_features (Float[Tensor, "... sequence_length d_in"]): Tensor to run your implementation on.
token_positions (Int[Tensor, " ... sequence_length"] | None): Optional tensor with the positions of the tokens
Returns:
Float[Tensor, " ... sequence_length d_out"]: Tensor with the output of running your optimized, batched multi-headed attention
implementation with the given QKV projection weights and input features.
"""
device, dtype = in_features.device, in_features.dtype
model = layer.CausalMultiheadSelfAttention(
d_model=d_model,
num_heads=num_heads,
theta=theta,
use_rope=(token_positions is not None),
max_seq_len=max_seq_len,
device=device,
dtype=dtype
)
model.load_state_dict({
"q_proj.W": q_proj_weight,
"k_proj.W": k_proj_weight,
"v_proj.W": v_proj_weight,
"o_proj.W": o_proj_weight,
}, strict=False)
return model(x=in_features, token_positions=token_positions)
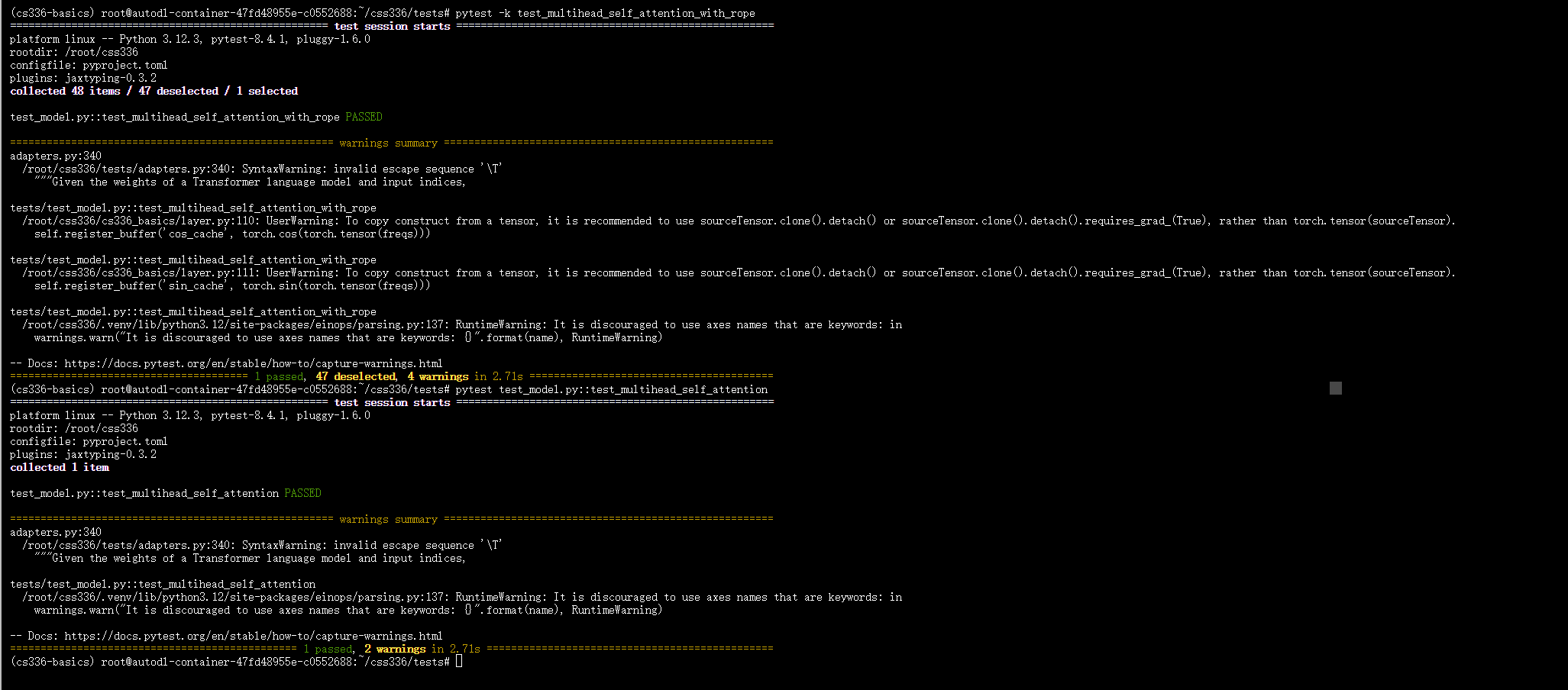
测试
pytest test_model.py::test_multihead_self_attention
pytest test_model.py::test_multihead_self_attention_with_rope
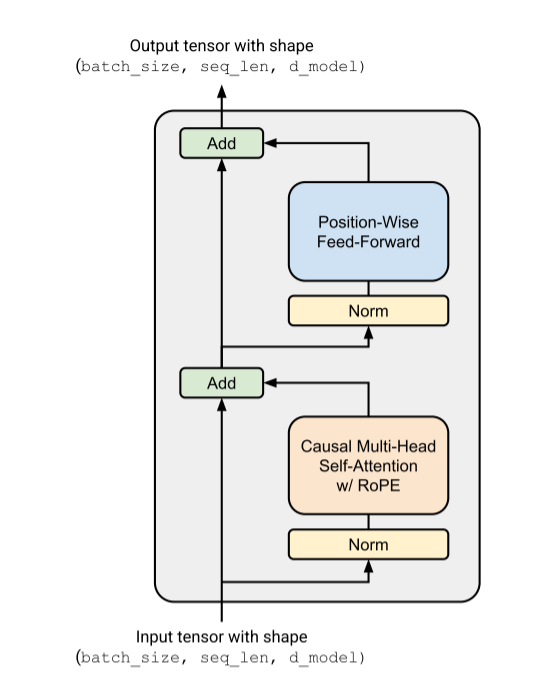
三、 The Full Transformer LM
Transformer block
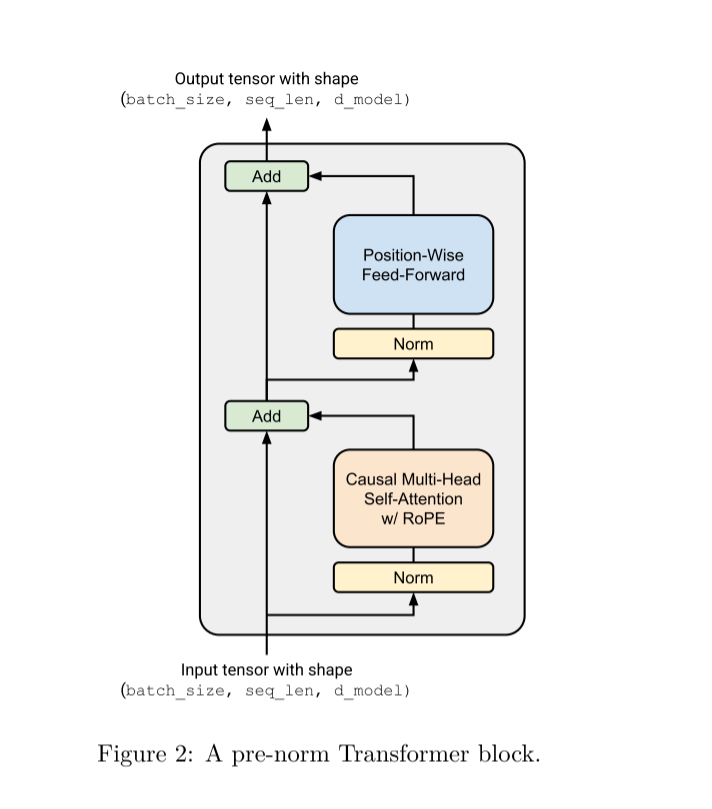
transformer block如上图所示,embedding x分成两条路线,一条通过RMSNorm再经过带有rope的causal MHA,另一条就是残差网络,直接和经过注意力路线的结果相加,然后得到的结果会再经过一个残差网络,残差网络还是先通过RMSNorm,再经过SiwshGLU,这构成了transformer block。
具体实现上就是将前面实现的模块组合到一起即可
class TransformerBlock(nn.Module):
def __init__(
self,
d_model: int,
num_heads: int,
d_ff: int,
max_seq_len: int,
theta: float = 10000.0,
use_rope: bool = True,
device: torch.device | None = None,
dtype: torch.dtype | None = None
):
super().__init__()
kwargs = {"device": device, "dtype": dtype}
self.d_model = d_model
self.num_heads = num_heads
self.norm1 = RMSNorm(
d_model=d_model,
device=device,
dtype=dtype
)
self.attn = CausalMultiheadSelfAttention(
d_model=d_model,
num_heads=num_heads,
max_seq_len=max_seq_len,
theta=theta,
use_rope=use_rope,
device=device,
dtype=dtype
)
self.norm2 = RMSNorm(
d_model=d_model,
device=device,
dtype=dtype
)
self.ffn = SwiGLU(
d_model=d_model,
d_ff=d_ff,
device=device,
dtype=dtype
)
def forward(
self,
x: Float[torch.Tensor, " batch seq_len d_model"],
token_positions: Int[torch.Tensor, "batch seq_len"]
) -> Float[torch.Tensor, " batch seq_len d_model"]:
b, s, _ = x.shape
attn_out = self.attn(self.norm1(x), token_positions=token_positions)
x = x + attn_out
ffn_out = self.ffn(self.norm2(x))
x = x + ffn_out
return x
这里有一个bug我调试了几个小时才发现,前面写的RMSNorm是有问题的,虽然单独的RMSNorm测试能通过但是组成Transformer block就会出问题。
class RMSNorm(nn.Module):
def __init__(
self,
d_model: int,
eps: float = 1e-5,
device: torch.device | None = None,
dtype: torch.dtype | None = None):
super().__init__()
self.d_model = d_model
self.eps = eps
factory_kwargs = {'device': device, 'dtype': dtype}
self.W = nn.Parameter(torch.ones(d_model, **factory_kwargs))
def forward(self, x: torch.Tensor) -> torch.Tensor:
in_dtype = x.dtype
x = x.to(torch.float32)
RMS = (x.pow(2).mean(dim=-1, keepdim=True) + self.eps).sqrt()
x /= RMS
x *= self.W
return x.to(in_dtype)
上面是之前的实现在forward的过程中我直接进行了下面操作,这是会有问题的
x /= RMS
因为残差网络的原因,x + attn(Norm(x)),RMSNorm对x进行归一化会导致第一个x也被进行了归一化,因为上面是原地操作的,这就和要求的数据流动不一样,我们希望第一个x是没有经过任何处理的,这样残差连接才能起到作用,保证梯度流畅。
于是进行了下面的修改
class RMSNorm(nn.Module):
def __init__(
self,
d_model: int,
eps: float = 1e-5,
device: torch.device | None = None,
dtype: torch.dtype | None = None):
super().__init__()
self.d_model = d_model
self.eps = eps
factory_kwargs = {'device': device, 'dtype': dtype}
self.W = nn.Parameter(torch.ones(d_model, **factory_kwargs))
def forward(self, x: torch.Tensor) -> torch.Tensor:
in_dtype = x.dtype
x = x.to(torch.float32)
RMS = (x.pow(2).mean(dim=-1, keepdim=True) + self.eps).sqrt()
normalized_x = x / RMS
results = normalized_x * self.W
return results.to(in_dtype)
adapters
def run_transformer_block(
d_model: int,
num_heads: int,
d_ff: int,
max_seq_len: int,
theta: float,
weights: dict[str, Tensor],
in_features: Float[Tensor, " batch sequence_length d_model"],
) -> Float[Tensor, " batch sequence_length d_model"]:
device, dtype = in_features.device, in_features.dtype
model = layer.TransformerBlock(
d_model=d_model,
num_heads=num_heads,
d_ff=d_ff,
use_rope=True,
max_seq_len=max_seq_len,
theta=theta,
device=device,
dtype=dtype
)
model.load_state_dict({
"attn.q_proj.W": weights["attn.q_proj.weight"],
"attn.k_proj.W": weights["attn.k_proj.weight"],
"attn.v_proj.W": weights["attn.v_proj.weight"],
"attn.o_proj.W": weights["attn.output_proj.weight"],
"norm1.W": weights["ln1.weight"],
"norm2.W": weights["ln2.weight"],
"ffn.linear1.W": weights["ffn.w1.weight"],
"ffn.linear2.W": weights["ffn.w2.weight"],
"ffn.linear3.W": weights["ffn.w3.weight"]}
, strict=False)
B, S, _ = in_features.shape
positions = torch.arange(S, device=device).expand(B, -1)
assert S <= max_seq_len, f"Sequence length {S} exceeds max_seq_len {max_seq_len}"
return model(in_features, token_positions=positions)
测试
pytest test_model.py::test_transformer_block
调试这个bug的时候调了3 4个小时一度给我调自闭了,相信jyy的三公理:
- 机器永远是对
- 没有测试的程序永远是错的
- 当一项工作令你感到tedious的时候,一定有更高效的解决方法
Transformer LM
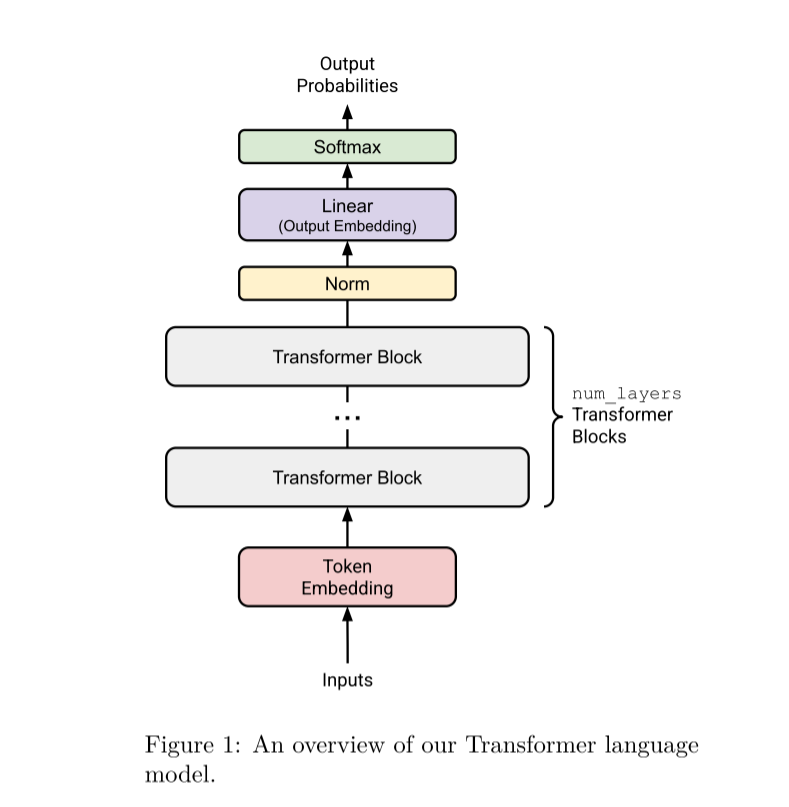
现在我们需要将整个Transformer language model给组合起来,即数据从被tokenizer划分成token_ids后开始处理,知道最后得到预测下一个词的logits。
有个点需要注意的是这里经过最后的Linear后不能再经过softmax不然会无法通过测试样例。
def _copy_param(target: torch.Tensor, source: torch.Tensor) -> None:
"""
Copy `source` into `target` in-place, transposing `source` if that
is what makes the shapes line up.
"""
if source.shape == target.shape:
target.data.copy_(source)
elif source.T.shape == target.shape:
target.data.copy_(source.T)
else:
raise ValueError(f"Shape mismatch: cannot load parameter of shape {source.shape} "
f"into tensor of shape {target.shape}")
class TransformerLM(nn.Module):
def __init__(
self,
vocab_size: int,
context_length: int,
d_model: int,
num_layers: int,
num_heads: int,
d_ff: int,
theta: float,
device: torch.device | None = None,
dtype: torch.dtype | None = None):
super().__init__()
self.vocab_size = vocab_size
self.context_length = context_length
self.d_model = d_model
self.num_layers = num_layers
self.num_heads = num_heads
self.d_ff = d_ff
self.theta = theta
factory_kwargs = {"device": device, "dtype": dtype}
self.emb = Embedding(
num_embeddings=vocab_size,
embedding_dim=d_model,
**factory_kwargs
)
self.blocks = nn.ModuleList([
TransformerBlock(
d_model=d_model,
num_heads=num_heads,
d_ff=d_ff,
max_seq_len=context_length,
theta=theta,
use_rope=True,
**factory_kwargs,
)
for _ in range(num_layers)
])
self.final_norm = RMSNorm(d_model=d_model,device=device,dtype=dtype)
self.final_linear = Linear(in_features=d_model, out_features=vocab_size, **factory_kwargs)
def forward(self, token_ids: Int[torch.Tensor, "batch seq_len"]) -> Float[torch.Tensor, "batch seq_len vocab_size"]:
B, S = token_ids.shape
assert S < self.context_length, "text is too long"
x = self.emb(token_ids)
pos = torch.arange(S).unsqueeze(0).expand(B, S)
for block in self.blocks:
x = block(x, pos)
x = self.final_norm(x)
x = self.final_linear(x)
# logits = softmax(x, dim=-1)
return x
adapters的编写
def run_transformer_lm(
vocab_size: int,
context_length: int,
d_model: int,
num_layers: int,
num_heads: int,
d_ff: int,
rope_theta: float,
weights: dict[str, Tensor],
in_indices: Int[Tensor, " batch_size sequence_length"],
) -> Float[Tensor, " batch_size sequence_length vocab_size"]:
"""Given the weights of a Transformer language model and input indices,
return the output of running a forward pass on the input indices.
This function should use RoPE.
Args:
vocab_size (int): The number of unique items in the output vocabulary to be predicted.
context_length (int): The maximum number of tokens to process at once.
d_model (int): The dimensionality of the model embeddings and sublayer outputs.
num_layers (int): The number of Transformer layers to use.
num_heads (int): Number of heads to use in multi-headed attention. `d_model` must be
evenly divisible by `num_heads`.
d_ff (int): Dimensionality of the feed-forward inner layer (section 3.3).
rope_theta (float): The RoPE $\Theta$ parameter.
weights (dict[str, Tensor]):
State dict of our reference implementation. {num_layers} refers to an
integer between `0` and `num_layers - 1` (the layer index).
The keys of this dictionary are:
- `token_embeddings.weight`
Token embedding matrix. Shape is (vocab_size, d_model).
- `layers.{num_layers}.attn.q_proj.weight`
The query projections for all `num_heads` attention heads.
Shape is (num_heads * (d_model / num_heads), d_model).
The rows are ordered by matrices of shape (num_heads, d_k),
so `attn.q_proj.weight == torch.cat([q_heads.0.weight, ..., q_heads.N.weight], dim=0)`.
- `layers.{num_layers}.attn.k_proj.weight`
The key projections for all `num_heads` attention heads.
Shape is (num_heads * (d_model / num_heads), d_model).
The rows are ordered by matrices of shape (num_heads, d_k),
so `attn.k_proj.weight == torch.cat([k_heads.0.weight, ..., k_heads.N.weight], dim=0)`.
- `layers.{num_layers}.attn.v_proj.weight`
The value projections for all `num_heads` attention heads.
Shape is (num_heads * (d_model / num_heads), d_model).
The rows are ordered by matrices of shape (num_heads, d_v),
so `attn.v_proj.weight == torch.cat([v_heads.0.weight, ..., v_heads.N.weight], dim=0)`.
- `layers.{num_layers}.attn.output_proj.weight`
Weight of the multi-head self-attention output projection
Shape is ((d_model / num_heads) * num_heads, d_model).
- `layers.{num_layers}.ln1.weight`
Weights of affine transform for the first RMSNorm
applied in the transformer block.
Shape is (d_model,).
- `layers.{num_layers}.ffn.w1.weight`
Weight of the first linear transformation in the FFN.
Shape is (d_model, d_ff).
- `layers.{num_layers}.ffn.w2.weight`
Weight of the second linear transformation in the FFN.
Shape is (d_ff, d_model).
- `layers.{num_layers}.ffn.w3.weight`
Weight of the third linear transformation in the FFN.
Shape is (d_model, d_ff).
- `layers.{num_layers}.ln2.weight`
Weights of affine transform for the second RMSNorm
applied in the transformer block.
Shape is (d_model,).
- `ln_final.weight`
Weights of affine transform for RMSNorm applied to the output of the final transformer block.
Shape is (d_model, ).
- `lm_head.weight`
Weights of the language model output embedding.
Shape is (vocab_size, d_model).
in_indices (Int[Tensor, "batch_size sequence_length"]) Tensor with input indices to run the language model on. Shape is (batch_size, sequence_length), where
`sequence_length` is at most `context_length`.
Returns:
Float[Tensor, "batch_size sequence_length vocab_size"]: Tensor with the predicted unnormalized
next-word distribution for each token.
"""
first_val = next(iter(weights.values()))
device, dtype = in_indices.device, first_val.dtype
model = layer.TransformerLM(
vocab_size=vocab_size,
context_length=context_length,
d_model=d_model,
num_layers=num_layers,
num_heads=num_heads,
d_ff=d_ff,
theta=rope_theta,
device=device,
dtype=dtype
).eval()
from layer import _copy_param
with torch.no_grad():
# (a) token embedding (also implicitly ties lm_head)
_copy_param(model.emb.W, weights["token_embeddings.weight"])
# (b) per-layer parameters
for layer_idx in range(num_layers):
pfx = f"layers.{layer_idx}."
block = model.blocks[layer_idx]
# ── attention projections
_copy_param(block.attn.q_proj.W, weights[pfx + "attn.q_proj.weight"])
_copy_param(block.attn.k_proj.W, weights[pfx + "attn.k_proj.weight"])
_copy_param(block.attn.v_proj.W, weights[pfx + "attn.v_proj.weight"])
_copy_param(block.attn.o_proj.W, weights[pfx + "attn.output_proj.weight"])
# ── RMSNorm weights
_copy_param(block.norm1.W, weights[pfx + "ln1.weight"])
_copy_param(block.norm2.W, weights[pfx + "ln2.weight"])
# ── feed-forward (SwiGLU) weights
_copy_param(block.ffn.linear1.W, weights[pfx + "ffn.w1.weight"])
_copy_param(block.ffn.linear2.W, weights[pfx + "ffn.w2.weight"])
_copy_param(block.ffn.linear3.W, weights[pfx + "ffn.w3.weight"])
# (c) final layer-norm
_copy_param(model.final_norm.W, weights["ln_final.weight"])
# (d) (optional) make sure tied output embedding matches lm_head if provided
_copy_param(model.final_linear.W, weights["lm_head.weight"])
# 3) run the forward pass and return logits
with torch.no_grad():
return model(in_indices) # (batch, seq_len, vocab_size)
测试命令
pytest test_model.py::test_transformer_lm
测试结果:

四、 完整代码
感觉transformer LM 架构更像是在搭乐高一样,不过实现的时候还是有很多细节,以及einops、pytorch语法上的使用、以及jaxtype。
测试本章所有模块
pytest test_model.py
最后完结撒花~~~~
完整代码放在github仓库,如果有需要可以start一下!!!
github仓库





















 1503
1503

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








