微电网两阶段鲁棒优化经济调度方法

1微电网系统建模

典型微网结构：

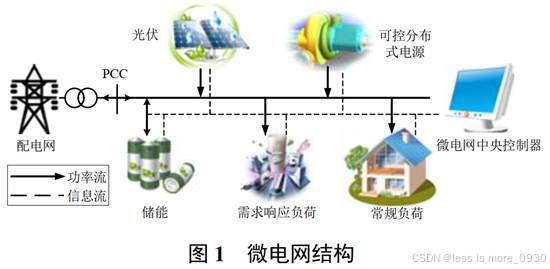
采用集中控制结构，第2日运行计划所需的决策信息有：

1. 第2日光伏出力和负荷功率预测曲线；
2. 需求侧响应可调度范围、单位调度成本和期望用电计划；
3. 配电网日前交易电价及各时段交互功率限值；
4. 储能与可控分布式电源容量、调度功率限值和单位调度成本；
5. 储能SOC限值及调度初期SOC；

1.1可控分布式电源

       考虑可控分布式电源为微型燃气轮机，用线性函数表示发电成本：

CG(t)表示微型燃气轮机在t时段的发电成本；a、b为成本系数；PG(t)为t时段微型燃气轮机的输出功率；Δt为调度步长，取值为1h。

       由于微型燃气轮机的功率响应速度相对于小时级调度而言较快，因此不考虑其爬坡率约束，仅考虑输出功率约束：

式中PGmax和PGmin表示微型燃气轮机的最大/最小输出功率，分别受其额定功率和最小负载率限制。

1.2储能

       主要考虑一次投资成本和运维成本，在投资回收期内t时段的平均充放电成本CS(t)可表示为：

式中：KS为折算后的单位充放电成本（就是指储能单元实际存储的功率变化量的单位成本，比如充放电效率为80%，负荷得到8W，则实际上储能单元内少了10W；电源提供了10W，实际上储能单元内多了8W。）；PSch(t)和PSdis(t)分别表示t时段储能逆变器交流侧输入/输出的充电/放电功率；η为储能单元的充放电效率。

       储能单元运行中需要满足（最大充放电功率限制、调度始末时刻储能存储电量相等方便循环调度、储能容量最大最小限值延长寿命）：

1.3需求侧响应负荷

       需求侧响应负荷用电特性约束（实际调度能量在最大最小可调度能量范围内）：

       t时段需求侧响应调度成本CDR(t)为：

KDR为需求响应负荷的单位调度成本；PDR(t)为t时段微电网对需求响应负荷的实际调度功率；PDR∗(t)为t时段需求响应负荷的期望用电功率。

       引入两个非负辅助变量PDR1(t)、PDR2(t)，将非线性表达式转换为线性形式：

1.4配电网互动功率

       交互功率平衡约束（购售之间的差值即为功率缺额）：

       功率交互值需满足：

PMmax为最大功率交互值；UM(t)=1，微电网从配电网购电；UM(t)=0，微电网向配电网售电。

       t时段配微交互成本CM(t)为：

λ(t)为配电网的日前交易电价。

2两阶段鲁棒优化模型

       目标函数为日运行成本最小化：

       约束条件包括：

       不考虑光伏出力和负荷功率的不确定性时，可得到上述微电网经济调度问题的确定性优化模型，其紧凑形式可表述为：

       优化变量x、y：

c：目标函数系数列向量；D、K、F、G和Iu为对应约束下变量的系数矩阵；d、h为常数列向量。         约束第四行为各时段光伏和负荷预测值：

       上述模型为混合整数线性规划问题（包含连续变量和整数变量的线性规划问题），可采用常规的确定性优化方法（利用问题的解析性质，产生一确定的有限或无限点序列使其收敛于全局最优解）进行求解，光伏和负荷的预测精度越高，调度方案越优。

       实际情况下微网运行存在大量不确定性，上述模型得到的方案就过于“冒险”，考虑光伏出力和负荷波动位于下式所构建的箱型不确定集U内：

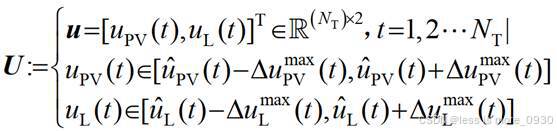
uPV(t)和uL(t)为考虑不确定性后引入的光伏出力和负荷功率不确定变量；ΔuPVmax(t)和ΔuLmax(t)分别表示光伏和负荷的最大波动偏差，均为正。

       为了找到不确定变量u在不确定集U内朝着最恶劣场景变化时经济性最优的调度方案，搭建两阶段鲁棒优化模型：

       min-max-min问题由外到里依次求解。第一阶段问题：第一个min是为了先确定优化变量x，给第二阶段最小化运行成本问题提供变量y的可行域。第二阶段问题：max表示的是不确定变量朝着最恶劣的场景变化，优化变量为u；第二个min表示最小化运行成本，优化变量为y。

       Ω(x,u)表示给定一组(x,u)时优化变量y的可行域，具体表达式如下：

式中γ，λ，ν，π表示第二阶段的最小化问题中各约束对应的对偶变量。

3求解算法

       列和约束生成（C&CG）算法通过将原问题分解为主问题和子问题进行交替求解的形式得到原问题的最优解。C&CG算法在求解主问题的过程中不断引入和子问题相关的变量和约束，获得更加紧凑的原目标函数值下界，从而有效降低迭代次数。

       对上式进行分解，可得主问题为：

式中：a表示的是在“最恶劣”情况下的运行成本，所以a大于等于所有情况下的运行成本，即a≥cTyl；yl为第l次迭代后子问题的解；ul*为第l次迭代后得到的最恶劣场景下不确定变量u的取值。k为当前的迭代次数。

       经分解后的子问题形式为：

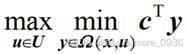
       当给定优化变量y的可行域Ω(x,u)后，微电网运行成本最小化是一个线性问题，根据强对偶理论和第二阶段最小化问题中各约束对应的对偶变量γ，λ，ν，π可将其转化为max问题，并将两个max问题合并可得：

推导过程：

       原问题为：

       可以得到拉格朗日函数为： 

       则拉格朗日对偶函数为：

       可得对偶问题的目标函数为：

       对偶问题的约束条件为（因为l为0等式的对偶变量，且对偶问题的目标函数中不存在变量l，故l自由。由于对偶函数中求极小值的部分是括号内的部分乘以矩阵y，而矩阵y的元素均为正，所以只需要令括号内的值非负，即存在下界，则问题有解）：

       汇总可得对偶问题为：

       将两个max问题进行合并，可得整个第二阶段的目标函数：

       由于新目标函数中存在双线性项uTπ，根据文献[2]可知，该对偶问题的最优解u*是不定集U的一个极点，即上式取得最大值时，不确定量u的取值应该是波动区间U的边界。在此处，光伏出力最小且负荷功率最大时，成本更高，场景“最恶劣”。再引入参数ΓPV和ΓL分别做为光伏出力和负荷功率的“不确定性调节参数”，取值范围是0~NT之间的整数，表示调度周期内光伏出力和负荷功率取到波动区间最小值和最大值的时段总数，用于调节最优解的保守性，取值越大越保守，越小越冒险。

式中：B=[BPV(t), BL(t)]T 为二进制变量，取值为1时相应时段的不确定变量即取到区间的边界。

       若直接将不确定变量U的表达式代入整个第二阶段的目标函数，会出现二进制变量和连续变量相乘的形式，引入辅助变量和相关约束对其进行线性化可得：

其中：Δu=[ΔuPVmax(t),ΔuLmax(t)]T，B′=[B′PV(t),B′L(t)]T为引入的连续辅助变量；π为对偶变量的上界，可取为足够大的正实数。

       经过上述推导和转换，两阶段鲁棒模型最终解耦为具有混合整数线性形式的主问题和子问题式：

随后可用C&CG算法进行求解，流程如下：

1. 给定一组不确定变量u的取值作为初始的最恶劣场景，设定调度方案对应的运行成本下界LB=-∞，上界UB=+∞，迭代次数k=1；
2. 根据最恶劣场景u1*求解主问题，得到最优解(xk*,ak*,y1*,…,yk*)，其中，主问题的目标函数值作为新的下界LB=ak*；
3. 将求得的主问题的解代入上式，求解子问题，得到子问题的目标函数值fk*(xk*)和相应的最恶劣场景下不确定变量u的取值uk+1*，更新上界UB=min{UB, fk*(xk*)}；
4. 给定算法的收敛阈值为ε，若UB-LB≤ε，则停止迭代，返回最优解xk*和yk*；否则增加变量yk +1及如下约束：

令k=k+1，跳转至2）直至算法收敛。

4算例分析

       以图 1 所示微电网为研究算例，验证本文所提出的两阶段鲁棒优化模型及求解算法的有效性。仿真分析包含微电网经济调度方案、储能调度边界条件和优化模型比较 3 个方面。

4.1微电网经济调度方案

       设定负荷功率不确定性调节参数ΓL为12，光伏不确定性调节参数ΓPV为6。储能的额定容量设为2MW⋅h，微电网的运行参数如表 1 所示。

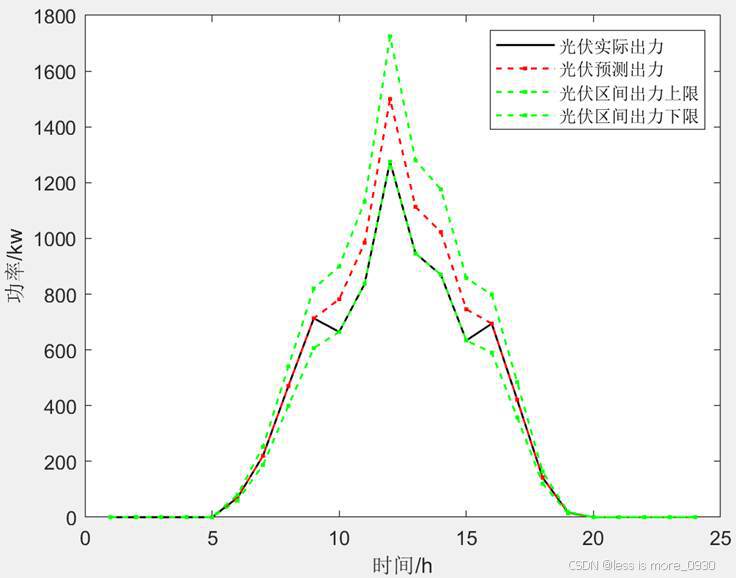
       根据历史数据，设定负荷功率和光伏出力的波动偏差分别为预测值的10%和15%。预测/实际负荷功率曲线及光伏出力曲线分别如图 2 和图 3 所示，阴影部分即为本文考虑的不确定集。

       将居民用电阶梯电价作为配电网和微电网进行功率交换的日前交易电价，如图 4 所示。

       调度优化结果如图 5—7 所示。

       1~7h及20~24h：光伏输出功率为0，依靠微型燃气轮机、储能及配电网供给。

       若交易电价低于微型燃气轮机单位发电成本，则微型燃气轮机以最小输出功率运行，否则输出最大功率，增加售电量或者降低购电量，降低成本。

       储能单元在谷电价时段存储电能，在峰电价时段售出，实现削峰填谷。

       在满足总用电量需求和各时段用电量约束的前提下，微电网将峰值时段的用电需求分配至谷值时段，降低微电网峰电价时段购电能。

4.2储能调度边界条件

       推导得到微电网使用储能进行削峰填谷的边界条件，即只有在调度储能有利于降低系统的运行成本时，微电网才会使用储能。其数学模型如下：

       不等式左侧为调度成本，右侧为获得的收益。λ1和λ2分别为谷时段和峰时段的交易电价。因为储能始末时刻电量相同：

        所以数学模型可以简化为：

上式即为为微电网使用储能的边界条件。

       以表 1 的参数为例，当KS的取值落于图 8 所示平面下方时，微电网调度储能才能降低总的运行成本。反之，微电网将不会安排储能的充放电计划。

       定义微电网在调度周期内对储能进行充电或者放电的总电量和储能额定容量的比值为储能使用率：

式中CSrate为储能的额定容量。当KS变化时，微电网对储能的使用率变化曲线如图 9 所示（整个  调度周期为24h，在此期间储能可能多次充放电，因此使用率可能大于1）。

       从图 9 中可以看出，当储能单位充放电成本大于￥0.39/(kW⋅h)时，微电网将不再对储能进行充放电。

4.3优化模型比较

       从确定最恶劣场景的有效性和调度方案的保守性及性能两个方面，对常规确定性优化模型和本文所提出的两阶段鲁棒优化模型进行比较。

       将确定性优化模型和两阶段鲁棒优化模型随机选取若干个相同时段，使不确定变量取到预测区间的边界，对比在最恶劣场景下的调度方案性能。

       ΓL=12，ΓPV=6。此时两阶段鲁棒优化对应的最恶劣场景为：负荷功率在 9~13h 及 17~23h 这 12 个时段取到预测区间的最大值，光伏出力在 10~14h 以及 16h 这 6个时段取到预测区间的最小值。

定义如下 3 种比较方案：

       方案1：负荷功率取为预测区间最大值的时段为8~14h以及19~23h，光伏出力的时段选取和两阶段鲁棒模型相同；

       方案2：负荷功率的时段选取和两阶段鲁棒模型相同，光伏出力取为预测区间最小值的时段为8~13h；

       方案3：负荷功率和光伏出力的时段选取和两阶段鲁棒模型相同。

       验证本文所提的优化方法可对调度方案的保守性进行灵活的调整，选取三组不确定性调节参数进行仿真对比，参数设置及相应的日前运行成本如表 3 所示。

       表3中不确定性调节参数等于 0 时，两阶段鲁棒优化模型等效于确定性优化。微电网在制定日前调度计划时考虑的不确定性越多，方案越保守，购电量越多，售电量越少，成本越高。虽然确定性优化方法得到的调度方案运行成本低于鲁棒优化方法，这并不意味着确定性优化方法的方案“优于”鲁棒方法。该方案对应于微电网在日前市场上提交的发用电计划，而由预测误差引起的计划发用电量和第2日实际发用电量之间的不平衡量需要由微电网在实时市场中进行补偿。实时市场的购电/售电电价一般要高于/低于日前市场，导致微电网最终交易成本增加。从这个角度说，鲁棒优化方法得到的调度方案具备更强的鲁棒性和抵御实时市场电价波动风险的能力。

       为了验证该能力，仍选择ΓL=12，ΓPV=6，假定实时市场中的购电/售电电价为日前市场相应时段电价的1.5/0.5倍。以图2、图3所示的负荷和光伏第2日的实际值/预测值作为参考，针对不同负荷及光伏预测误差下鲁棒优化方法和确定性优化方法的最终运行成本如表5所示。

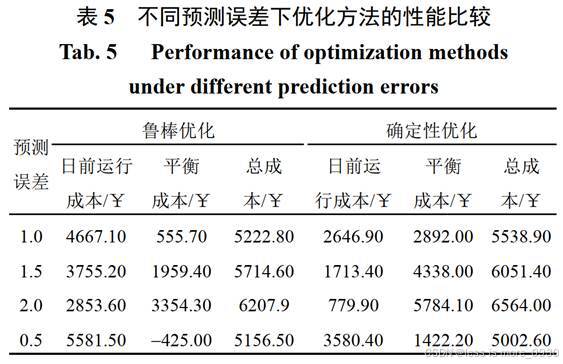
       表5中，预测误差表示负荷和光伏各时段的预测值偏离实际值的程度相対于参考曲线的倍数，取值为 1 时等同于图 2 和图 3 所示的预测曲线。尽管在图2和图3所示参考预测曲线下，鲁棒优化方法得到的日前调度方案具有更高的日前运行成本(￥4667.1)，但因其考虑了负荷功率和光伏出力的不确定性，在实时市场中因预测误差引起的不平衡量要低于确定性优化方法，如图 10 所示，正值表示微电网在实时市场中需要额外购买的功率，负值表示微电网额外出售的功率。采用鲁棒优化方法得到的日前调度方案在实时市场中购入的功率小于确定性优化方法，因此其平衡成本为￥555.7，远低于确定性优化方法(￥2892)，从而降低了最终的运行成本。

        预测误差增大(1.5/2)，确定性优化方法平衡成本显著增大(￥4338/￥5784.1)，虽然采用鲁棒优化方法得到的日前调度方案对应的平衡成本也有所提高(￥1959.4/￥3354.3)，但其总运行成本依然低于确定性优化方法，且降低运行成本的效果更加明显。当预测精度较高时(预测误差取值为0.5)，由于预测曲线和实际曲线之间的偏差较小，确定性优化方法得到的调度方案更加接近实际运行情况，对应的平衡成本降低。此时鲁棒优化方法因其制定的日前调度方案过于“保守”，存在富余的功率在实时市场中以较低的价格出售，使得总运行成本较确定性优化方法有所提高。

5仿真复现

流程图：

（1）程序主要由初始化、主循环和结果呈现3部分组成；

（2）在初始化过程中求解问题时考虑光伏出力和负荷的不确定性，在主循环中求解时不考虑；

（3）代码中子问题的目标函数与论文中不同；

论文中：

代码中：

（4）只设定了4次循环，在达到4次循环之前就实现了收敛。

复现结果：

（1）经过2次主循环后，上下界不再更新；

（2）微型燃气轮机以1~7h 、24h最小输出功率，8~23h输出最大功率，与论文结论一致；

（3）用电低谷期从配电网购电，用电高峰期向配电网售电，与论文结论一致。

（1）储能在用电低谷充电，在用电高峰放电，与论文结论一致；

（2）需求响应负荷实际调度功率和期望用电计划；

（3）光伏出力在10-15h这6个时段取得出力最小值。

6结论

       本文基于两阶段鲁棒优化方法建立了考虑微电网内可再生分布式电源和负荷不确定性的经济调度模型，分析结果表明：

1）模型考虑光伏和负荷的不确定性，求解可得“最恶劣”场景下系统运行成本最小的调度方案；

2）提出不确定性调节参数，可调整方案保守性，利于调度在成本和风险间合理选择；

3）鲁棒优化方法得到的日前调度方案具备更强的鲁棒性和抵御实时市场电价波动风险的能力；

4）储能的调度边界条件为规划储能和设置激励机制提供参考。

       但也存在一些不足：

1）“最恶劣”情况下不确定性取的是区间边界，在线性系统中有效，在非线性系统不一定成立；

2）建模中未考虑网损，且仅考虑了4个部分，考虑的内容较少。 

参考文献

1. 刘一欣,郭力,王成山.微电网两阶段鲁棒优化经济调度方法[J].中国电机工程学报,2018,38(14):4013-4022+4307.
2. Bertsimas D, Litvinov E, Sun X A, et al. Adaptive robust optimization for the security constrained unit commitment problem[J]. IEEE transactions on power systems, 2012, 28(1): 52-63.