（复现）微电网两阶段鲁棒优化经济调度方法

前置条件

1.写出所有目标函数，等式约束，不等式约束的一般形式。
2.写出紧凑形式（矩阵表示）。
3.列写主问题，子问题及子问题的对偶问题。

程序改动

类似Ky=0的问题就不提了，说一下对仿真结果影响大的一个因素。

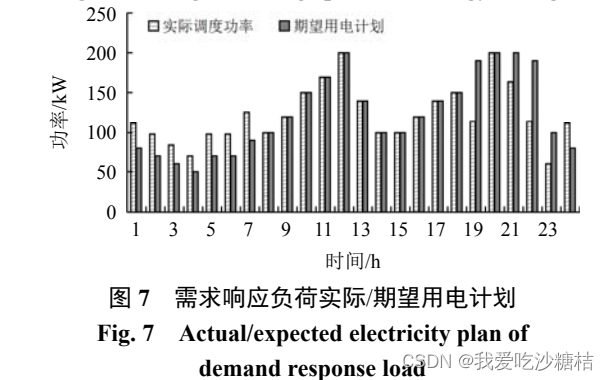
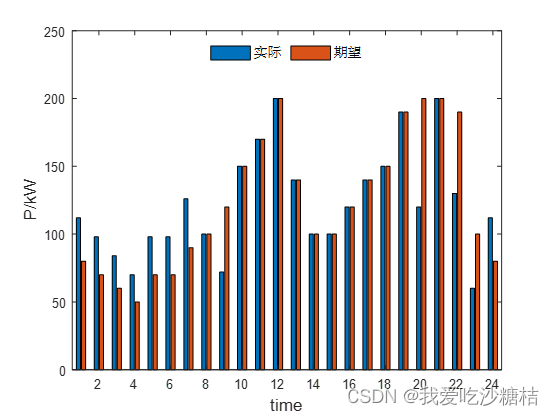
可以明显发现，夜间的需求响应实际调度功率并没有像文章中公式（13）P_DR(1)>=0，P_DR(2)>=0那么简单，为了经济最大化会直接到200的。其原因就在于文中少了对其上限的约束，对比发现，可以考虑加入一个系数表明最大转入转出的上限，笔者选取了0.4，没有过多的细究，感兴趣的可以自己摘取所有数据比对一下。

遇到过的问题集合

1.把主要内容注释掉了

2.输入矩阵错误

3.目标函数最大值的的的语句
optimize(Constraints,-Objective,options);%-1表示最大值

4.关于$\Delta$u
文中给的都是正值，但为了保证加号的统一性，$\Delta$u中光伏取负，负荷取正。

5.线性化问题或者子问题求解小于0
参见文献[1],[2]

仿真结果

1.收敛过程

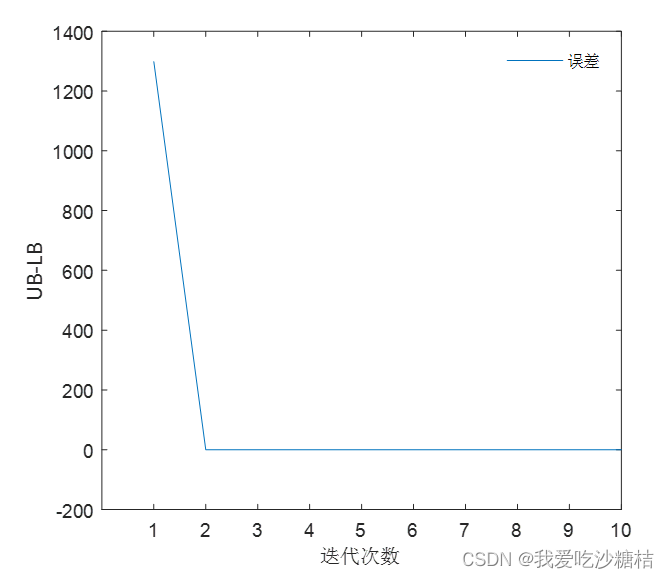
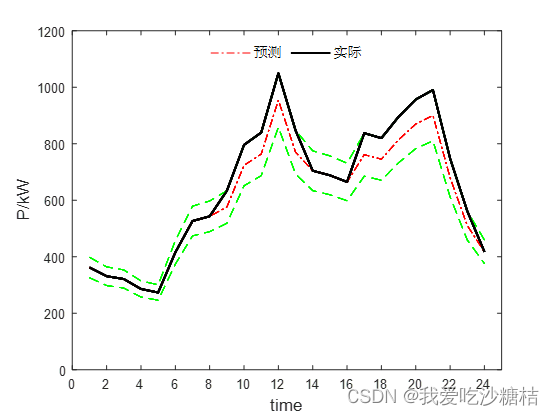
2.最恶劣情景

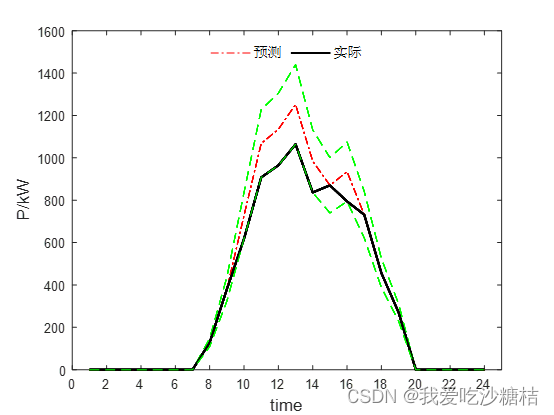
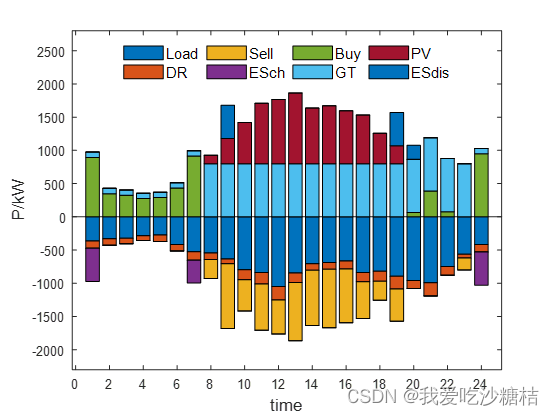
3.调度结果

4.需求响应

说明

1.只能大概获得数据，其结果为4593.62（原文4667.10）。
2.需要讨论可以私信；需要代码可以直接加微信，平台不让传（微信：Oranger345）。

参考文献

[1]刘一欣,郭力,王成山.微电网两阶段鲁棒优化经济调度方法[J].中国电机工程学报,2018,38(14):4013-4022
[2]任郡枝. 光伏配电网中储能系统规划方法研究[D].山东大学,2020.