第十九届同济大学程序设计竞赛暨高校网络友谊赛 G-归零（可持久化权值线段树）

TP

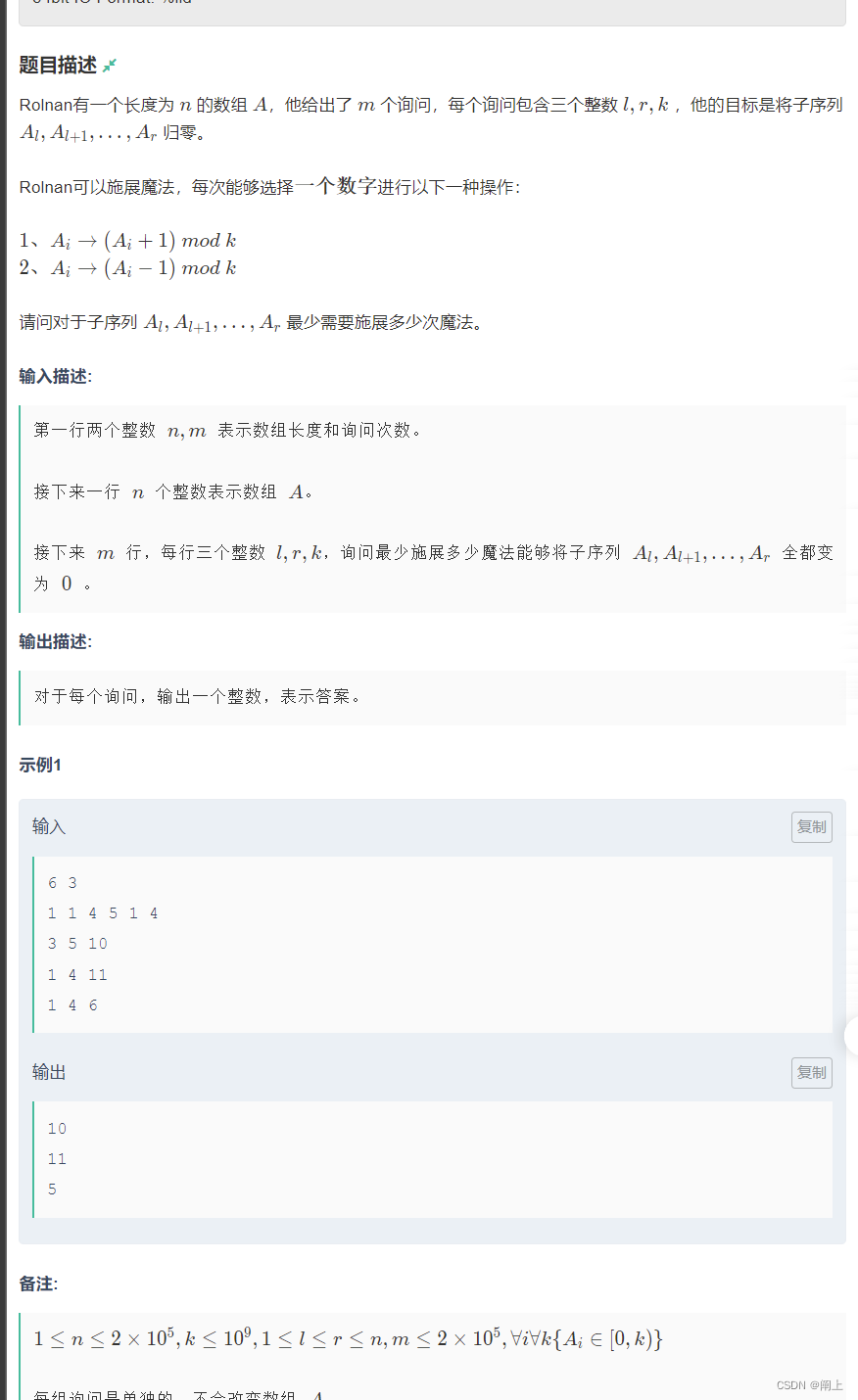
• 漏看了一个很重要的东西，询问保证区间段每个 Ai 都小于 k，这样就不用考虑比 k 大取模的情况了

• 自然可以想到把 Ai 进行分类，分成 小于等于 k/2 和大于 k/2 来分别处理

• 普通线段树处理不了，所以考虑可持久化权值线段树

eg：

无需把 root[0] 整棵树建出来，动态开点就行，如果要建就需要vec离散化了

update 取地址传递会更快

因为动态开点的缘故，直接传入大范围的 l、r 也无妨，最多也就开出 log 的深度

$Code:$

#include<bits/stdc++.h>
#include<unordered_map>
#define debug cout << "debug---  "
#define debug_ cout << "\n---debug---\n"
#define oper(a) operator<(const a& ee)const
#define forr(a,b,c) for(int a=b;a<=c;a++)
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define all(a) a.begin(),a.end()
#define sz(a) (int)a.size()
#define endl "\n"
#define ul (u << 1)
#define ur (u << 1 | 1)
using namespace std;

typedef unsigned long long ull;
typedef long long ll;
typedef pair<ll, ll> PII;

const int N = 2e5 + 10, M = 2e6 + 10, mod = 1e9 + 7;
int INF = 0x3f3f3f3f; ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, B = 10, ki;

int a[N];
struct node
{
    int l, r;
    ll sum, cnt;
}tr[N * 50];
int root[N], idx;

//取地址
void update(int& u, int pre, int l, int r, int x) {
    u = ++idx;
    tr[u] = tr[pre];
    tr[u].cnt++, tr[u].sum += x;
    if (l == r)return;

    int mid = l + r >> 1;
    if (x <= mid)update(tr[u].l, tr[pre].l, l, mid, x);
    else update(tr[u].r, tr[pre].r, mid + 1, r, x);
}
ll query1(int u, int pre, int l, int r, int le, int re) {
    if (l >= le && r <= re)return tr[u].sum - tr[pre].sum;
    int mid = l + r >> 1;
    ll t = 0;
    if (le <= mid)t += query1(tr[u].l, tr[pre].l, l, mid, le, re);
    //写成 else if 改半天
    if (re > mid)t += query1(tr[u].r, tr[pre].r, mid + 1, r, le, re);
    return t;
}
ll query2(int u, int pre, int l, int r, int le, int re, int k) {
    if (l >= le && r <= re) { //范围别错了
        return (tr[u].cnt - tr[pre].cnt) * k - (tr[u].sum - tr[pre].sum);
    }
    int mid = l + r >> 1;
    ll t = 0;
    if (le <= mid)t += query2(tr[u].l, tr[pre].l, l, mid, le, re, k);
    if (re > mid)t += query2(tr[u].r, tr[pre].r, mid + 1, r, le, re, k);
    return t;
}

void solve() {
    cin >> n >> m;

    int len = 1e9;//权值线段树直接开了 1e9 范围
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        update(root[i], root[i - 1], 0, len, a[i]);
    }

    while (m--)
    {
        int l, r, k;
        cin >> l >> r >> k;

        ll ans = 0;
        ans += query1(root[r], root[l - 1], 0, len, 0, k / 2);
        ans += query2(root[r], root[l - 1], 0, len, k / 2 + 1, k, k);
        cout << ans << endl;
    }
}

int main() {
    cinios;
    int T = 1;
    for (int t = 1; t <= T; t++) {
        solve();
    }
    return 0;
}
/*
*/