数学基础
定义:
- 标量定义: 日常生活中常用的单个数字,如游戏中英雄的智力值 10、敏捷值 6、力量值
- 向量定义: 将多个标量用中括号括起来组成的数组,如英雄属性[10,6,2]。
- 矩阵定义: 将多个向量按行排列组成的矩形数组,如四个英雄的属性组成的 4×3 矩。
- 特殊关系: 向量是矩阵的特殊形式,每个向量都是 1×3 的矩阵。
- 排列方式: 行向量是数字横向排列,列向量是数字纵向排列,矩阵可视为行向量或列向量的组合。
表示:
- 标量表示: 使用小写字母xi , j表示,下标 i,j 表示矩阵中第 i 行第 j 列的元素。
- 向量表示: 使用大写字母 下带 标Xi表示矩阵中的第 i 行向量。
- 矩阵表示: 使用大写字母 X 表示,n×m 矩阵全体记为Rn × m(数矩)。
下标含义: 在Xi中,i 表示矩阵的第 i 行;在xi , j中,i,j 表示第 i 行第 j 列的元素。
标量知识点总结
标量乘法
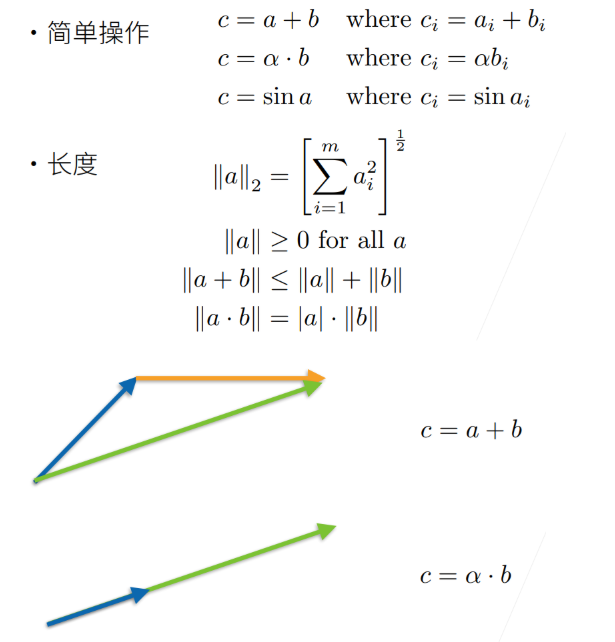
向量知识点总结
参考:
https://www.bilibili.com/video/BV11RPVe7Eqi/?spm_id_from=333.337.search-card.all.click
表示方法:
单位向量
向量的⻓度
类似勾股定理
向量之间的运算
向量加法
向量减法
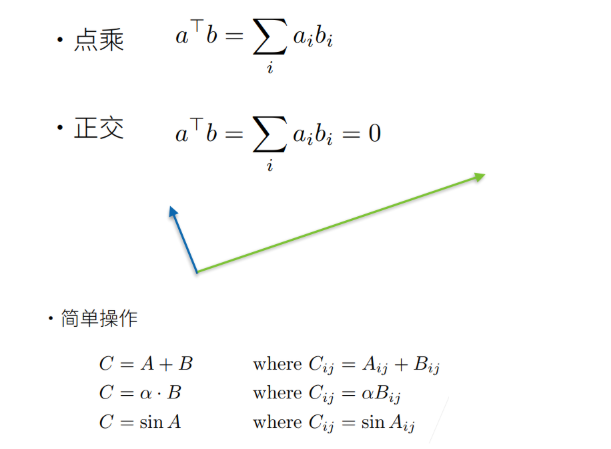
向量相乘的两种⽅式
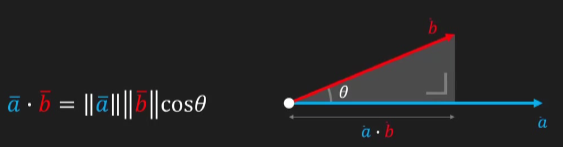
点积:
叉积:
别名:向量积(vector product),结果为向量
三维公式
矩阵知识点总结
特殊矩阵
单位矩阵: n×n 方阵,对角线元素为 1,其余为 0,记作I n。
对角矩阵: n×n 方阵,非对角线元素全为 0,对角线元素可以不全相等。
三角矩阵: 分为上三角矩阵(下半部分为 0)和下三角矩阵(上半部分为 0),对角矩
阵同时属于两者。
矩阵的运算
矩阵的加法和减法
前提条件: 要求两个矩形状相同(行数和列数分相等)
运算规则: 对应元素相加减,结果保持相同维度。
运算性质: 满足加法交换律(X+Y=Y+X)和结合律((X+Y)+Z=X+(Y+Z))。
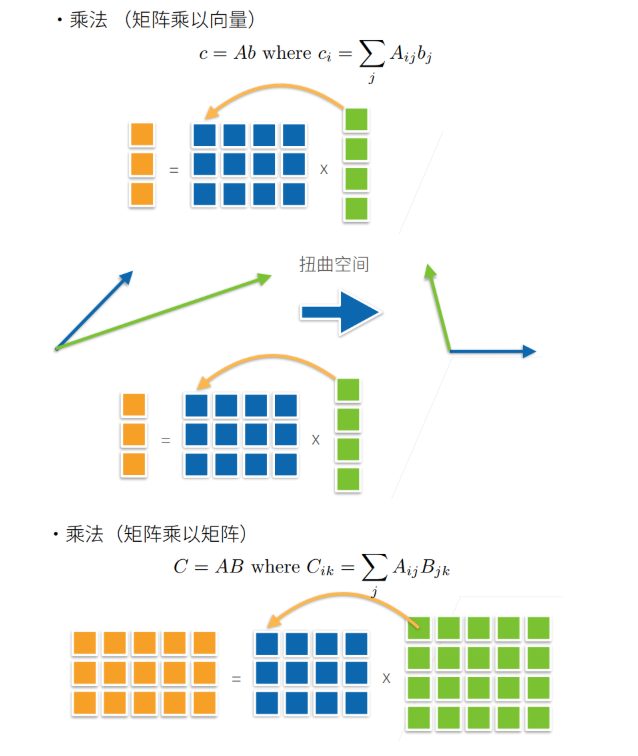
矩阵的乘法
运算规则: 矩阵每个元素乘以该数字,如kX =(kxi , j )。
Hadamard 乘积方法:
标准矩阵乘法:
条件: 第一个矩阵的列数等于第二个矩阵的行数
维度: n×p 矩阵乘以 p×m 矩阵得到 n×m 矩阵
性质: 满足结合律和分配律,但不满足交换律
应用价值: 简化线性模型表示,如将 y1=ax1 +b和 y2=ax2 +b表示为Y = Xβ
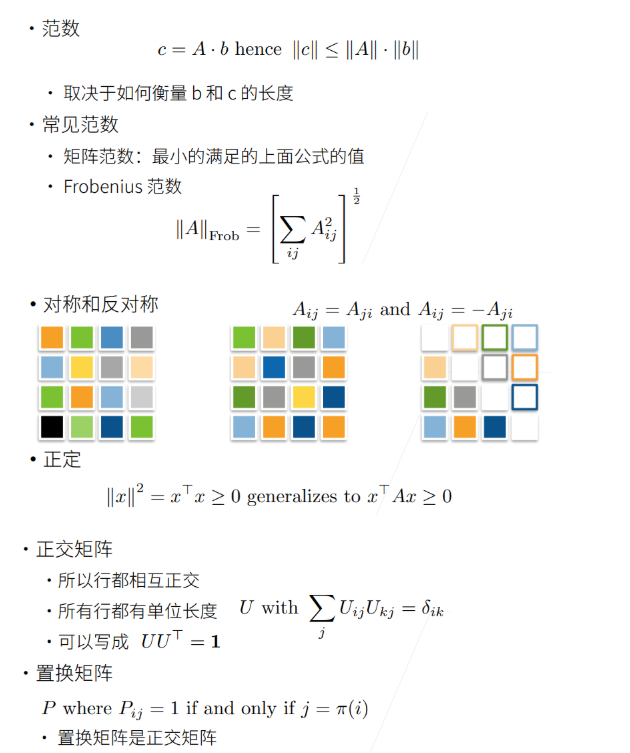
逆矩阵和转置
逆矩阵:
转置:
对称矩阵: 满足 A^T = A的方阵,对角线两侧元素对称相等。
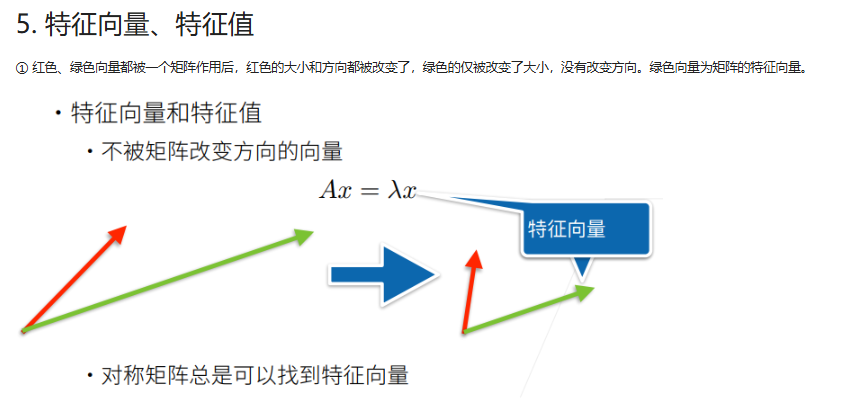
图像总结
深度学习的应用:










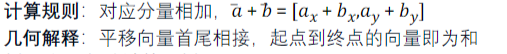





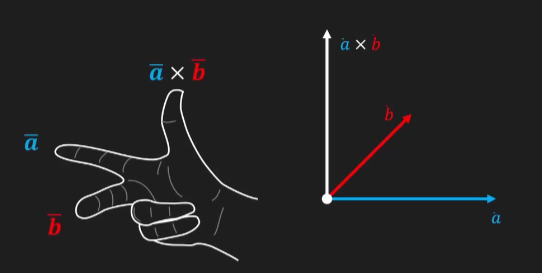






















 442
442

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








