基于候鸟优化算法（MBO）的柔性车间调度优化研究（Matlab代码实现）

最新推荐文章于 2025-01-29 22:11:18 发布

荔枝科研社

最新推荐文章于 2025-01-29 22:11:18 发布

阅读量1.6k

点赞数

分类专栏：优化求解(Matlab代码与讲解) 车间调度(Matlab代码与讲解) 文章标签： matlab 算法开发语言候鸟优化算法柔性车间调度

本文链接：https://blog.youkuaiyun.com/weixin_46039719/article/details/127803367

版权

优化求解(Matlab代码与讲解) 同时被 2 个专栏收录

138 篇文章

订阅专栏

车间调度(Matlab代码与讲解)

29 篇文章

订阅专栏

本文探讨了FJSP-LS问题中的批次划分方案，利用候鸟优化算法（MBO）进行深入研究。MBO算法因其优点在生产线调度中表现出色。博客详细介绍了算法流程，包括领飞鸟进化、跟飞鸟进化、竞争机制及全局最优解的求解过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

📋1 概述

📝2 运行结果

📃3 参考文献

📋4 Matlab代码实现

📋1 概述

在FJSP-LS求解方法上，现有研究主要采用元启发式算法，如遗传算法、差分算法、禁忌搜索[1,8J和粒子群算法[)等，大多侧重于调度方案的优化，对批次划分方案的制定缺乏深入研究。候鸟优化(Migrating Birds Optimization,MBO)算法是DUMAN等于2011年首先提出的自然启发的元启发式算法，具有参数少、易于理解、结构简单等优点，成功用于多种优化问题，尤其是求解二次分配问题时，该算法获得了比模拟退火算法、禁忌搜索算法和指导的进化模拟退火算法质量更高的解。同时，越来越多的学者尝试将MBO运用到生产线调度上，同样获得了高质量的解，本文基于候鸟优化算法（MBO）的柔性车间调度优化研究。

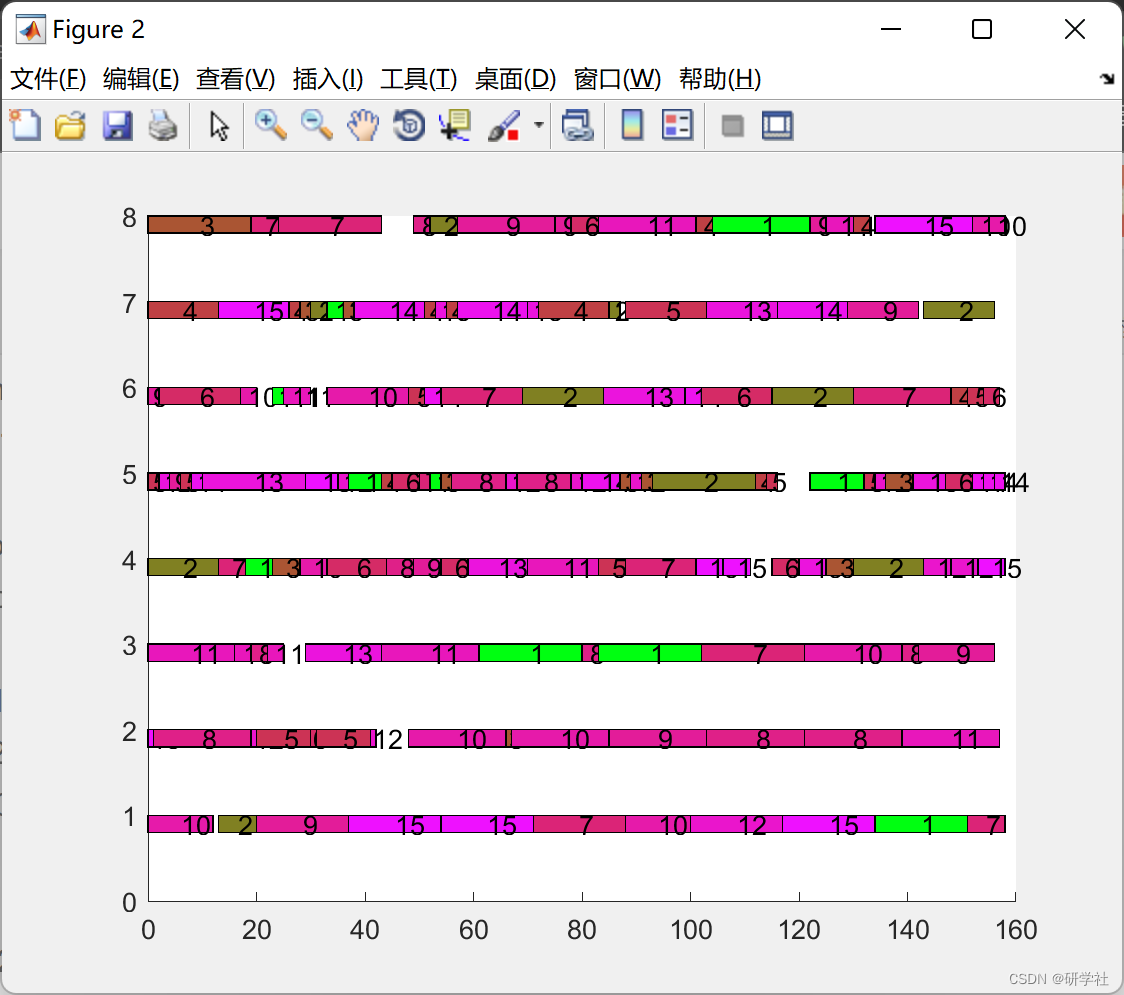
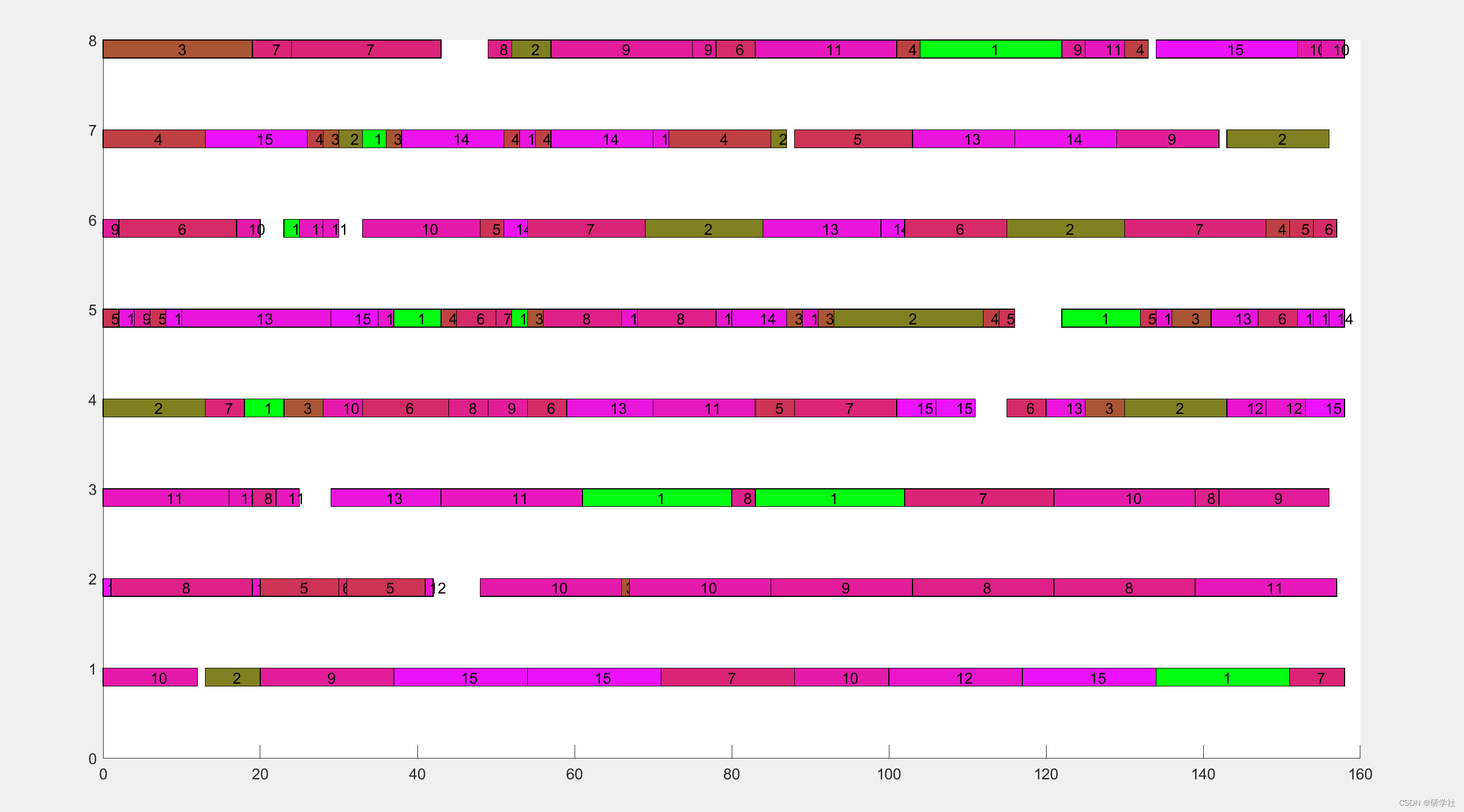
📝2 运行结果

%% 巡回阶段
for i=1:G
%% 领飞鸟进化
[leader,Z_leader,share,Z_share]=bird_evolution(leader,Z_leader,[],[],...
N_size,S_size,total_op_num,num_machine,e,num_job,num_op);
%% 跟飞鸟进化
% 初始化左右队列的共享解集
share_left=share;
Z_share_left=Z_share;
share_right=share;
Z_share_right=Z_share;
for j=1:sp
% 左队列
[lefts(j,:),Z_left(j),share_left,Z_share_left]=bird_evolution(lefts(j,:),Z_left(j),share_left,Z_share_left,...
N_size-S_size,S_size,total_op_num,num_machine,e,num_job,num_op);
% 右队列
[rights(j,:),Z_right(j),share_right,Z_share_right]=bird_evolution(rights(j,:),Z_right(j),share_right,Z_share_right,...
N_size-S_size,S_size,total_op_num,num_machine,e,num_job,num_op);
end
%% 竞争机制2：队间交叉
% 随机产生G2对位置相同的个体
ind=randperm(sp,G2);
[rights(ind,:),Z_right(ind),lefts(ind,:),Z_left(ind)]= crossover(lefts(ind,:),rights(ind,:),...
Z_left(ind),Z_right(ind),total_op_num,num_machine,e,num_job,num_op);
end
%% 竞争机制1：队内竞争
ind=randperm(sp,G1);
% 左队列
[~,ind1]=sort(Z_left(ind));
lefts(ind,:)=lefts(ind(ind1),:);
Z_left(ind)=Z_left(ind(ind1));
% 右队列
[~,ind2]=sort(Z_right(ind));
rights(ind,:)=rights(ind(ind2),:);
Z_right(ind)=Z_right(ind(ind2));
%% 领飞鸟替换
if rand<0.5
% 选择左队列首只跟飞鸟
[leader,Z_leader,lefts,Z_left]=update_leader(leader,Z_leader,lefts,Z_left);
else
% 选择右队列首只跟飞鸟
[leader,Z_leader,rights,Z_right]=update_leader(leader,Z_leader,rights,Z_right);
end
%% 记录相关数据
% 记录每代的最优适应度与平均适应度
Z=[Z_leader,Z_left,Z_right];
[val,ind]=min(Z);
trace(1,gen)=val;
trace(2,gen)=mean(Z);
% 更新全局最优适应度
if gen==1 || MinVal>trace(1,gen)
MinVal=trace(1,gen);
end
end

%% ============================输出结果=============================
%% 输出最优适应度
fprintf('最优适应度：'),disp(MinVal)
%% 绘制最优适应度与平均适应度的迭代曲线图
figure(1)
plot(trace(1,:));
hold on;
plot(trace(2,:),'-.');grid;
legend('解的变化','种群均值的变化');
%% 绘制全局最优解的甘特图
[Z,~,~,machine_time,Pvals]=fitness(leader,num_machine,e,num_job,num_op);
Pval1=Pvals{1,1};
figure(2);
for i=1:total_op_num
mText=leader(total_op_num+i);
b=leader(i);
x1=Pval1(1,i);
x2=Pval1(2,i);
y1=mText-0.2;
y2=mText;
hold on;
fill([x1,x2,x2,x1],[y1,y1,y2,y2],[1-1/b,1/b,b/num_job]);
text((x1+x2)/2,mText-0.1,num2str(b));
end