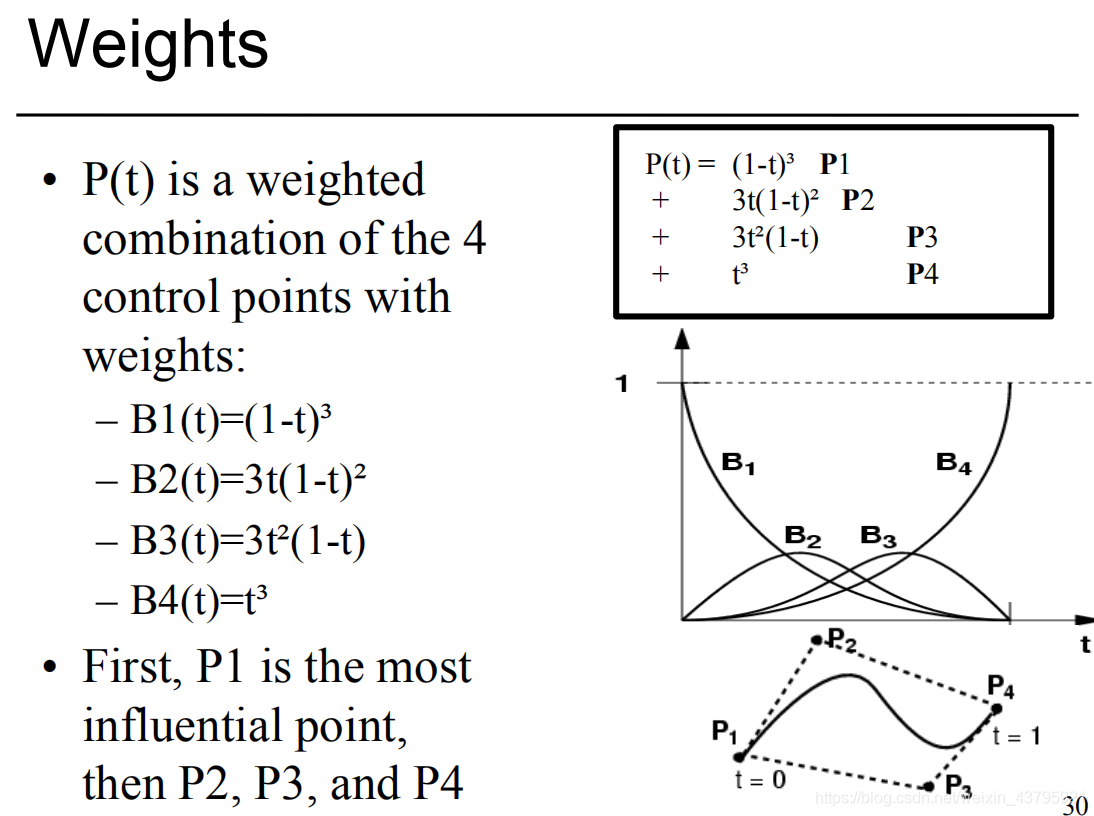
用权重的概念理解三次贝塞尔曲线,三次贝塞尔曲线综合了插值(Interpolation)和近似(Approximation),各点前面的多项式是点的权重(也可以把点看成权重,多项式看成是基,该被称为Bernstein polynomials)。起点和终点是在曲线上的,中间两个点是近似的。P1处的切线过P2,P4处的切线过P3。
样条曲线更一般的形式如下图,其中T(t),代表最原始的基向量,B代表一个可以将原始的基向量构造出来新的基的矩阵,可以构成不同类型的样条曲线,G代表给定的原始点。

 本文深入探讨了三次贝塞尔曲线的数学原理,解释了如何通过权重概念理解曲线形状,以及曲线如何结合插值和近似特性。文章还介绍了样条曲线的一般形式,包括基向量、基矩阵和给定点在曲线生成中的作用。
本文深入探讨了三次贝塞尔曲线的数学原理,解释了如何通过权重概念理解曲线形状,以及曲线如何结合插值和近似特性。文章还介绍了样条曲线的一般形式,包括基向量、基矩阵和给定点在曲线生成中的作用。
用权重的概念理解三次贝塞尔曲线,三次贝塞尔曲线综合了插值(Interpolation)和近似(Approximation),各点前面的多项式是点的权重(也可以把点看成权重,多项式看成是基,该被称为Bernstein polynomials)。起点和终点是在曲线上的,中间两个点是近似的。P1处的切线过P2,P4处的切线过P3。

样条曲线更一般的形式如下图,其中T(t),代表最原始的基向量,B代表一个可以将原始的基向量构造出来新的基的矩阵,可以构成不同类型的样条曲线,G代表给定的原始点。

 2526
2526
 3193
3193

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


