预后建模绕不开的lasso cox回归

欢迎关注”生信修炼手册”!

回归我们并不陌生，线性回归和最小二乘法，逻辑回归和最大似然法，这些都是我们耳熟能详的事物，在生物信息学中的应用也比较广泛, 回归中经常出现两类问题，欠拟合和过拟合。

对于欠拟合，简单而言就是我们考虑的少了，一般通过在回归模型中增加自变量或者扩大样本数量来解决；对于过拟合，简单而言就是考虑的太多了，模型过于复杂了，这时候可以对已有的自变量进行筛选，在代价函数中增加惩罚项来限制模型的复杂度，增加的惩罚项我们称之为正则化，正则化常用的有L1正则化和L2正则化，

所谓正则化Regularization, 指的是在回归模型代价函数后面添加一个约束项， 在线性回归模型中，有两种不同的正则化项

1. 所有参数绝对值之和，即L1范数，对应的回归方法叫做Lasso回归

2. 所有参数的平方和，即L2范数，对应的回归方法叫做Ridge回归，岭回归

lasso回归对应的代价函数如下

岭回归对应的代价函数如下

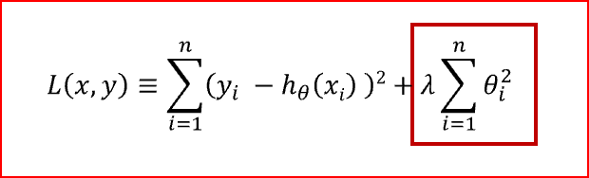
红框标记的就是正则项，需要注意的是，正则项中的回归系数为每个自变量对应的回归系数，不包含回归常数项。

在预后建模的文章中，我们需要针对多个marker基因的表达量汇总形成一个指标，使用该指标来作为最终的maker, 而这个指标在文章中被称之为各种risk score, 比如NAD+基因的预后模型，构建的maker就叫做NPRS, 全称的解释如下 

The NAD+ metabolism-related prognostic risk score (NPRS) of each sample was calculated using the formula: NPRS = ΣExp (mRNAί) × Coefficient (mRNAί)

所以各种的预后建模，其实都是lasso回归技术在生物信息学领域的应用。注意观察上述的Lasso回归代价函数，，可以看到有一个未知数λ， 这个参数是一个惩罚项的系数，数值越大，惩罚项对应的影响就越大，我们求解的目标是代价函数值最小，λ = 0时，惩罚项失去意义，代价函数变成了普通的线性回归，而λ过大，惩罚项的影响被放的过大，过小时，惩罚项又失去了原本的意义，所以使用lasso回归，