《Polygon Mesh Processing》_第四章_平滑

4.0 写在前面

在第三章引入了微分几何学，我们能够将曲面表示为离散的面后，第四章我们学习平滑技术，来应对离散和出现的粗糙的噪点问题。最小化过程通常涉及曲率或高阶导数。我们将证明网格平滑技术直接计算迭代去噪过程的极限曲面，这揭示了这两种方法之间的联系。

4.1 傅里叶变换与流形调和函数

使用傅里叶变换可以对一维函数$f(x)$进行低通滤波。

4.1.1

4.1.2

4.2 流形调和函数

傅里叶变换将单变量函数 $f:\mathbb{R}\to \mathbb{C}$ ，即从其在空间域中的表示 $f(x)$ 映射到其在频率域中的表示 $F(\omega )$。该变换及其逆变换可表示为
$$F(\omega )={\int }_{-\infty }^{\infty }f(x)e^{-2\pi i\omega x}dx,(4.1)$$

$$f(x)={\int }_{-\infty }^{\infty }F(\omega )e^{2\pi i\omega x}d\omega .(4.2)$$

这些方程具有直观的几何解释：函数 f(x)可被视为某一向量空间（可积复值函数空间）中的元素，该向量空间配备了内积
$$⟨f,g⟩={\int }_{-\infty }^{\infty }f(x)\overline{g(x)}dx,$$
其中 $\overline{(a+ib)}=(a-ib)$ 表示复共轭。复指数函数(高斯公式)
$$e_{\omega }(x):=e^{2\pi i\omega x}=\cos (2\pi \omega x)-i\sin (2\pi \omega x)$$
由频率为 $\omega$ 的正弦函数和余弦函数构成，因此被视为频率为 $\omega$ 的复波。它们构成了该向量空间中与频率相关的正交基——即频率域。

在此背景下，傅里叶变换本质上是通过将“向量”$f$ 正交投影到“基向量”$e_{\omega }$ 上实现的基变换：
$$f(x)=\sum _{\omega =-\infty }^{\infty }⟨f,e_{\omega }⟩e_{\omega }.$$
标量系数 $⟨f,e_{\omega }⟩$ 正是式 (4.1) 中的 $F(\omega )$。它描述了基函数 $e_{\omega }$ 在 $f$ 中所占的比重，即信号 $f(x)$ 中包含频率为 $\omega$ 的成分的幅值。由于频率 $\omega$ 是实数值而非仅为整数，上述方程中的求和运算需转化为积分运算，由此可推导出式 (4.2)。

由于基 $e_{\omega }$ 对应的坐标 $F(\omega )$ 直接与频率相关，我们只需截断所有高于用户定义阈值 ${\omega }_{\text{max}}$ 的频率，即可实现理想低通滤波。这等效于仅利用低频成分 $|\omega |<{\omega }_{\text{max}}$ 重构滤波后的函数 $\tilde{f}$：
$$\tilde{f}(x)={\int }_{-{\omega }_{\text{max}}}^{{\omega }_{\text{max}}}⟨f,e_{\omega }⟩e_{\omega }d\omega .\text{\hspace{1em}(4.3)}$$

4.1.2 流形调和函数

现在需将一维傅里叶框架推广到定义在（离散）二维流形表面上的函数 $f:S\to \mathbb{R}$。式 (4.1) 所示的傅里叶变换无法直接推广到流形上的函数。而以下观察结果填补了这一空白：正弦函数和余弦函数（进而复波 $e_{\omega }$）是拉普拉斯算子的特征函数，即
$$\Delta \left(e^{2\pi i\omega x}\right)=\frac{d^2}{d{x}^2}{e}^{2\pi i\omega x}=-{\left(2\pi \omega \right)}^2{e}^{2\pi i\omega x}.$$

若函数 $e_i$ 满足 $\Delta e_i={\lambda }_i{e}_i$，则 $e_i$ 是拉普拉斯算子（Laplacian）的特征函数（eigenfunction），对应的特征值（eigenvalue）为 ${\lambda }_i$，这与矩阵的特征向量满足 $A{e}_i={\lambda }_i{e}_i$ 的性质类似。

因此，一维傅里叶变换的基函数是拉普拉斯算子的特征函数。由此可见，选择二维流形表面上拉普拉斯-贝尔特拉米算子（Laplace-Beltrami operator）的特征函数作为广义基函数，是一种自然的思路。由于我们已经掌握了拉普拉斯-贝尔特拉米算子的离散化方法，这一思路也能将傅里叶变换推广到离散三角形网格上。

这一想法还与双变量表面上其他与频率相关的基函数相契合：对于二维正方形，拉普拉斯-贝尔特拉米算子的特征函数对应离散余弦变换（Discrete Cosine Transform，JPEG格式即采用该变换）的基函数；对于球面，其特征函数则对应球谐函数（spherical harmonics）。因此，拉普拉斯-贝尔特拉米算子的特征函数将这些概念推广到了任意二维流形表面，故而被称为流形调和函数（manifold harmonics）。

在三角形网格的离散化场景中，我们将连续函数 $f(x)$ 替换为其在 $n$ 个网格顶点处的采样值向量，即：
$$f:S\to \mathbb{R}⟶(f(v_1),\dots ,f(v_n){)}^T\text{\hspace{1em}(4.4)}$$

此时，拉普拉斯-贝尔特拉米算子 $\Delta$ 转化为拉普拉斯-贝尔特拉米矩阵 $L$，该矩阵可计算每个顶点的拉普拉斯值：
$$\left(\begin{array}{c}\Delta f(v_1)\\ ⋮\\ \Delta f(v_n)\end{array}\right)=L\left(\begin{array}{c}f(v_1)\\ ⋮\\ f(v_n)\end{array}\right)$$

该矩阵的第 $i$ 行包含了顶点 $v_i$ 处拉普拉斯离散化所需的权重 $w_{ij}$（详见3.3节与附录A.1），即：
$$\Delta f(v_i)=\sum _{v_j\in {\mathcal{N}}_1(v_i)}{w}_{ij}(f(v_j)-f(v_i))$$

此处假设权重未通过顶点价（vertex valence）或沃罗诺伊面积（Voronoi area）进行归一化，而是选择能使矩阵 $L$ 满足对称性的权重形式。例如，均匀拉普拉斯算子（uniform Laplacian）的权重取 $w_{ij}=1$，余切离散化（cotangent discretization）的权重取 $w_{ij}=(\cot {\alpha }_{i,j}+\cot {\beta }_{i,j})$（关于离散化与对称化的详细分析，可参考[Vallet and L´evy 08]）。

连续场景下拉普拉斯-贝尔特拉米算子的特征函数 $e_{\omega }(x)$，在离散场景中转化为拉普拉斯矩阵的特征向量 $e_1,\dots ,e_n$：一个 $n$ 维特征向量 $e_i$ 可视为连续特征函数 $e_i(x)$ 的离散采样（形式如式(4.4)所示），即 $(e_i(v_1),\dots ,e_i(v_n){)}^T$。特征向量 $e_i$ 的第 $k$ 个分量对应波 $e_i$ 在顶点 $v_k$ 处的幅值；而波的频率则由对应的特征值 ${\lambda }_i$ 决定。因此，矩阵 $L$ 的特征向量被称为三角形网格的“固有振动（natural vibrations）”，特征值则被称为“固有频率（natural frequencies）”[Taubin 95, Taubin 00]。图4.2展示了这种“流形调和基”[Vallet and L´evy 08]的部分基函数，颜色值代表每个顶点处的幅值。

（图4.2：流形调和基函数的部分元素。颜色值可理解为网格几何上驻波的幅值。图片来源：[Vallet and L´evy 08]，模型由比萨视觉计算实验室（Pisa Visual Computing Lab）提供。）

由于矩阵 $L$ 是对称半正定矩阵（详见附录A.1），其特征向量构成 ${\mathbb{R}}^n$ 的一组正交基，因此任意向量 $f=(f_1,\dots ,f_n{)}^T$ 都可在该基下精确表示为：
$$f=\sum _{i=1}^n⟨e_i,f⟩e_i$$
其中 $⟨e_i,f⟩=e_i^{T}f$。式(4.3)所示低通滤波的离散形式，是仅利用低频基函数（即前 $m<n$ 个特征向量）重构滤波后的函数 $\tilde{f}$：
$$\tilde{f}=\sum _{i=1}^m⟨e_i,f⟩e_i$$

（图4.3：使用越来越多的流形调和基函数得到的重构结果。图片来源：[Vallet and L´evy 08]，模型由比萨视觉计算实验室提供。）

（图4.4：一旦计算出流形调和基与对应的变换，便可结合用户定义的传递函数执行通用卷积滤波：低通滤波（左）、高通滤波（中）、增强滤波（右）。图片来源：[Vallet and L´evy 08]，模型由比萨视觉计算实验室提供。）

若将上述公式中的 $f$ 替换为包含所有顶点 $x$、$y$、$z$ 坐标的 $n$ 维向量，即可实现网格几何的滤波或平滑。图4.3显示，随着流形调和基函数数量的增加，重构得到的网格包含的几何细节也越来越丰富。最后，与傅里叶变换类似，通过基于用户定义的传递函数对各个频率 $F(\omega )$ 分别进行衰减或增强，可轻松实现通用卷积滤波（如图4.4所示）。

流形调和函数为傅里叶变换提供了自然推广，使其可应用于任意几何形状与拓扑结构的连续及离散二维流形表面。它支持利用精确截止频率 ${\omega }_{\text{max}}$ 实现理想低通滤波，也可实现灵活的卷积滤波。遗憾的是，该方法在许多应用场景中成本过高——因为对可能规模极大的拉普拉斯矩阵 $L$ 进行特征向量分解，在数值计算层面存在较大难度[Vallet and L´evy 08]。

下一节将介绍一种成本更低、更实用的方法——扩散流（diffusion flow）。该方法通过用高斯核（Gaussian kernel）对高频成分进行衰减，而非严格截断所有高于阈值 ${\omega }_{\text{max}}$ 的频率。由于频率域中高斯函数的逆傅里叶变换在空间域中仍为高斯函数，因此该方法无需进行傅里叶变换，可直接在空间域（即三角形网格上）计算平滑效果[Taubin 95]。

4.2 扩散流(diffusion flow)

扩散流是描述给定信号$f(x,t)$随时间平滑过程的数学模型，其理论已十分成熟。许多物理过程都可用扩散流描述（例如热扩散、布朗运动）。扩散流由扩散方程建模：
$$\frac{\partial f(x,t)}{\partial t}=\lambda \Delta f(x,t).\text{\hspace{1em}(4.5)}$$

该方程是二阶线性偏微分方程（PDE），其含义为：函数$f$随时间的变化量等于标量扩散系数$\lambda$与它的空间拉普拉斯算子$\Delta f$的乘积。例如，若$f(x,t)$表示时刻$t$下物质点$x$的温度，该方程则描述了物体内热量随时间的扩散过程，因此也被称为热传导方程。

我们可将扩散方程用于平滑流形表面$S$上的任意函数$f:S\to \mathbb{R}$，只需将常规拉普拉斯算子替换为流形上的拉普拉斯-贝尔特拉米算子即可。由于式(4.5)是连续的时变偏微分方程，我们需对其进行空间和时间两方面的离散化处理。

空间离散化时，我们再次将函数$f$替换为其在网格顶点处的采样值向量$(f(v_1,t),\dots ,f(v_n,t){)}^T$，并采用均匀离散化或余切离散化方法（见3.3节）计算离散拉普拉斯-贝尔特拉米算子。由此可得到每个顶点函数值的演化方程：
$$\frac{\partial }{\partial t}f(v_i,t)=\lambda \Delta f(v_i,t),i=1,\dots ,n,\text{\hspace{1em}(4.6)}$$
利用附录A.1中讨论的拉普拉斯矩阵$L$，该方程可表示为矩阵形式：$\frac{\partial f(t)}{\partial t}=\lambda Lf(t)$。

时间离散化时，我们将时间轴划分为大小为$h$的规则时间间隔，得到时间步序列{t,t+h,t+2h,… }\{t, t+h, t+2h, \dots\}{t,t+h,t+2h,…}。采用有限差分法近似时间导数（$\frac{\partial f(t)}{\partial t}\approx \frac{f(t+h)-f(t)}{h}$），并求解$f(t+h)$，可得到显式欧拉积分公式：
$$f(t+h)=f(t)+h\cdot \frac{\partial f(t)}{\partial t}=f(t)+h\lambda Lf(t).$$

需注意，为保证数值积分的稳定性，必须选择足够小的时间步长$h$。若要在较大时间步长下仍保证无条件稳定性，则需采用隐式时间积分方法[Desbrun et al. 99]。将拉普拉斯算子$\Delta f$的计算时刻从当前时刻$t$改为下一时刻$t+h$，可得到隐式欧拉积分公式：
$$f(t+h)=f(t)+h\lambda Lf(t+h)\iff (\text{Id}-h\lambda L)f(t+h)=f(t).$$

需注意，此时需求解一个稀疏$(n\times n)$线性方程组，才能得到函数值$f(t+h)$。附录中详细介绍了该线性方程组的构造方法及可行的求解算法。即便使用高效求解器，隐式积分的复杂度仍远高于显式积分，但它能保证数值稳定性。

若要平滑网格几何$x$（而非任意函数$f$），只需将上述更新规则应用于顶点位置向量$(x_1,\dots ,x_n{)}^T$即可。由此得到的“拉普拉斯平滑”，其顶点级显式更新公式为：
$$x_i\leftarrow x_i+h\lambda \Delta x_i.$$

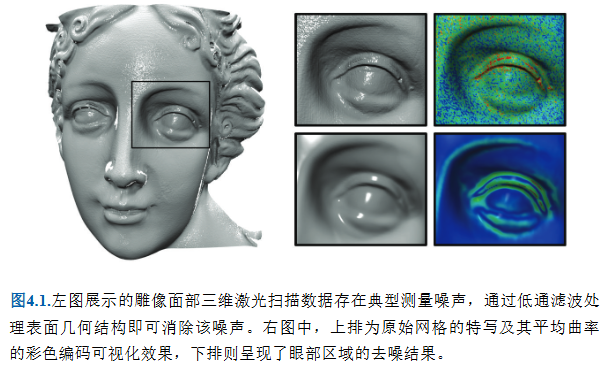
由于顶点位置的拉普拉斯-贝尔特拉米算子对应平均曲率法向量（$\Delta x=-2Hn$，见式(3.7)），所有顶点都会沿法向量方向移动，移动量由平均曲率$H$决定。因此，上述流方程也被称为平均曲率流[Desbrun et al. 99]。图4.1和图4.5展示了部分示例。

但需注意，顶点沿法向量方向移动这一特性（仅）对余切拉普拉斯算子近似成立。对于均匀拉普拉斯算子（见式(3.10)），该特性并不成立——因为均匀拉普拉斯算子未考虑网格几何信息，因此是对真实拉普拉斯-贝尔特拉米算子的一种精度较低的离散化。采用均匀拉普拉斯算子的拉普拉斯平滑，会试图将每个顶点移动到其1-环邻域顶点的重心位置。这一过程不仅能平滑网格几何，同时还会使三角剖分产生切向松弛（见图4.6）。根据具体应用场景，这一特性可能是优势（例如在6章的各向同性重划分中），也可能是劣势。

最后需说明，还可使用高阶拉普拉斯流$\frac{\partial f}{\partial t}=\lambda {\Delta }^{k}f$，其中高阶拉普拉斯算子的离散化通过递归计算得到：${\Delta }^{k}f=\Delta ({\Delta }^{k-1}f)$（见A.1节）。高阶流的计算成本更高（因其依赖更大的顶点模板），但具备更优的低通滤波特性[Desbrun et al. 99]。实际应用中，双拉普拉斯平滑（$k=2$）是计算效率与平滑质量之间的良好折中方案。若仅对局部区域应用平滑，双拉普拉斯平滑能使平滑区域与固定区域之间实现$C^1$连续过渡，而拉普拉斯平滑仅能实现$C^0$边界连续。

（图4.5 兔子网格的曲率流平滑效果：左图为原始网格，中图为10次迭代后结果，右图为100次迭代后结果。颜色编码表示平均曲率。（模型由斯坦福计算机图形实验室提供。））

（图4.6 对左图物体进行10次平滑迭代的效果：采用均匀拉普拉斯算子会同时规整三角剖分（中图），而采用余切拉普拉斯算子则能保留三角形形状（右图）。）

高阶拉普拉斯流可通过递归方式定义：${\Delta }^{k}f=\Delta ({\Delta }^{k-1}f)$（见A.1节）。高阶流的计算成本更高，因为它们依赖更大的顶点模板，但同时具备更优的低通滤波特性[Desbrun et al. 99]。在实际应用中，双拉普拉斯平滑（$(k=2)$）是计算效率与平滑质量之间的良好折中方案。若仅对局部区域应用平滑，双拉普拉斯平滑能使平滑区域与固定区域之间形成$C^1$连续过渡，而拉普拉斯平滑仅能实现$C^0$边界连续性。

4.3 表面光顺（Fairing）

扩散流(diffusion flow)方法的主要用途是从信号中去除高频噪声，同时保留其低频成分。
与之不同，表面光顺的目标是生成尽可能平滑的形状。如何实际衡量“平滑度”或“光顺度”，显然取决于具体应用，但总体而言，光顺曲面应遵循最简形状原则：曲面应不含任何不必要的细节或波动[Moreton and Séquin 92, Welch and Witkin 92]。

这一目标可通过设计合适的能量函数来实现——该能量函数会惩罚曲面不符合美观的形态。在用户定义的约束条件下，最小化这种光顺能量，最终即可得到期望的形状。表面光顺的典型应用包括构建平滑过渡曲面，以及用平滑补片填充孔洞，如图4.7所示。

接下来，我们先针对光滑参数化曲面$x:\Omega \to S$进行推导，之后再讨论离散三角形网格的情况。常用的光顺泛函之一是膜能量：
$$E_M(x)={\iint }_{\Omega }\sqrt{\text{det}(I)}dudv,\text{\hspace{1em}(4.7)}$$

该能量用于衡量曲面$S$的面积（参见式(3.3)）。我们需要在用户定义的约束条件下最小化该能量，这些约束通常是固定曲面边界$\partial \Omega$上的点坐标$x(u,v)$。面积最小的曲面对应于“固定的肥皂泡”，这类曲面被称为膜曲面或极小曲面。

遗憾的是，式(4.7)所示的能量具有高度非线性——它包含（本身已非线性的）第一基本形式行列式的平方根。这使得该能量的高效且稳健的最小化在数值计算层面极具挑战性。因此，我们对膜能量进行线性化处理：用一阶偏导数替代第一基本形式，得到狄利克雷能量：
$${\tilde{E}}_M(x)={\iint }_{\Omega }\Vert x_u{\Vert }^2+\Vert x_v{\Vert }^{2}dudv,\text{\hspace{1em}(4.8)}$$
其中我们采用简化记号$x_u=\partial x/\partial u$、$x_v=\partial x/\partial v$。由于偏微分是线性算子，该能量关于$x$是二次的。

为最小化上述线性化能量，我们采用变分法[Gelfand and Fomin 00, Kobbelt 97]。我们先以式(4.8)的一维形式引入变分法：寻找函数$f:[a,b]\to \mathbb{R}$，使其最小化一维膜能量：
$$E(f)={\int }_a^b(f_x{)}^{2}dx,$$
且满足边界约束（固定$f(a)$和$f(b)$的值）。假设$f$确实是$E(f)$的极小值点，若选取任意满足$u(a)=u(b)=0$的函数$u(x)$，则有$E(f)<E(f+u)$。进一步地，若将$E(f+\lambda u)$视为标量参数$\lambda$的函数，则该函数在$\lambda =0$处取得最小值。因此，其对$\lambda$的导数在$\lambda =0$处必须为零：
$${\frac{\partial E(f+\lambda u)}{\partial \lambda }|}_{\lambda =0}={\int }_a^{b}2f_x{u}_x=0.$$

图4.7 表面光顺的应用包括：在给定曲面部分之间构建平滑过渡（左图），以及用平滑补片填充孔洞（右图）。

通过分部积分并利用$u(a)=u(b)=0$的条件，可将上式转化为$-{\int }_a^b{f}_{xx}u=0$。这意味着，对于任意满足$u(a)=u(b)=0$的函数$u$，积分${\int }_a^b{f}_{xx}u$都必须为零。而这只有在以下条件成立时才可能实现：
$$f_{xx}=\Delta f=0.$$

这就是能量最小化问题$E(f)\to \text{min}$对应的欧拉-拉格朗日方程。直观而言，该方程表明：在极小值点$f$处，能量$E(f)$对$f$的一阶导数必须为零。由于$E(f)$是泛函（函数的函数），因此得到的方程是偏微分方程（PDE）。基于这一结论，我们无需对$E(f)$进行数值最小化，只需求解欧拉-拉格朗日方程即可得到极小值函数$f$。

将上述机制应用于式(4.8)的最小化时，需采用更复杂的边界约束，并利用散度定理而非分部积分。最终得到的欧拉-拉格朗日方程为：
$${\tilde{E}}_M(x)\to \text{min}⟺\Delta x(u,v)=0(\forall (u,v)\in \Omega ),$$
同样需满足边界$\partial \Omega$上的约束条件。

最后，我们将这一连续形式推广到离散三角形网格：（1）将连续坐标函数$x(u,v)$替换为顶点坐标向量$x=(x_1,\dots ,x_n{)}^T$；（2）采用离散拉普拉斯-贝尔特拉米算子。由此得到线性拉普拉斯方程组：
$$Lx=0,$$
求解该方程组即可得到最优顶点位置$x$（数值求解细节参见附录）。图4.8（左图）展示了离散膜曲面的示例。

图4.8 蓝色区域通过最小化光顺泛函确定：膜曲面（$\Delta x=0$，左图）、薄板曲面（${\Delta }^{2}x=0$，中图）、最小变化曲面（${\Delta }^{3}x=0$，右图）。欧拉-拉格朗日方程${\Delta }^{k}x=0$的阶数$k$决定了边界处的最大平滑度$C^{k-1}$。（图片来源：[Botsch and Kobbelt 04a]。版权所有©2004 ACM, Inc. 经许可收录于此。）

若目标是最小化曲率而非表面积，则从非线性薄板能量入手：
$$E_{\text{TP}}(x)={\iint }_{\Omega }{\kappa }_1^2+{\kappa }_2^{2}dudv,$$
其中${\kappa }_1$和${\kappa }_2$表示主曲率。线性化处理时，用二阶导数替代曲率，得到：
$${\tilde{E}}_{\text{TP}}(x)={\iint }_{\Omega }\Vert x_{uu}{\Vert }^2+2\Vert x_{uv}{\Vert }^2+\Vert x_{vv}{\Vert }^{2}dudv.$$

对应的欧拉-拉格朗日方程为$\Omega$内的${\Delta }^{2}x(u,v)=0$，同时需满足合适的$C^1$边界约束——即固定边界$\partial \Omega$上的点坐标$x(u,v)$和法向量$n(u,v)$。推广到离散三角形网格时，得到线性双拉普拉斯方程组：
$$L^{2}x=0.$$

在离散场景中，通常更简便的做法是固定边界顶点的两环位置，而非为一环边界顶点同时指定位置和法向量[Kobbelt et al. 98b]。如图4.8（中图）所示，这两种边界约束都能实现（近似的）$C^1$边界平滑度。

若要实现更高阶的光顺，需最小化的不是曲率本身，而是曲率变化率：
$${\iint }_{\Omega }{\left(\frac{\partial {\kappa }_1}{\partial t_1}\right)}^2+{\left(\frac{\partial {\kappa }_2}{\partial t_2}\right)}^{2}dudv,\text{\hspace{1em}(4.9)}$$
其中${\kappa }_1$、${\kappa }_2$仍表示主曲率，$t_1$、$t_2$表示对应的主曲率方向。这类所谓“最小变化曲面”[Moreton and Séquin 92]的离散近似，可通过求解六阶偏微分方程${\Delta }^{3}x=0$得到（见图4.8（右图））。

综上，我们可通过求解阶数分别为1、2、3的线性拉普拉斯方程组$L^{k}x=0$，得到膜曲面、薄板曲面和最小变化曲面。图4.9展示了不同拉普拉斯-贝尔特拉米离散化方法对薄板能量最小化结果的影响：均匀拉普拉斯算子在顶点密度变化较大的区域会产生伪影，而余切离散化方法能得到符合预期的结果。

表面光顺与扩散流之间存在一个有趣的联系：对于上述光顺曲面，其全表面上的$k$阶拉普拉斯算子${\Delta }^{k}x$均为零（由构造方式决定）。由于$k$阶拉普拉斯算子也是$k$阶拉普拉斯流的更新向量，因此这些光顺曲面是流$\partial x/\partial t={\Delta }^{k}x$的稳态。这一特性验证了光顺曲面确实是“尽可能平滑”的。此外，$k$阶拉普拉斯流的一个显式时间步，等效于求解线性方程组${\Delta }^{k}x=0$的一次（阻尼）雅可比迭代（参见附录）。若采用无穷大时间步长$h=\infty$进行一次隐式时间步计算，可直接得到${\Delta }^{k}x=0$。因此，拉普拉斯流会收敛到光顺曲面。

最后需说明的是，上述框架同样可用于构建光顺的一般函数$f:S\to {\mathbb{R}}^d$，只需将坐标函数$x$替换为$f$即可。后续章节中还会用到这些概念：计算最小畸变参数化（$\Delta u=0$，见第5章）、最小化拉伸与弯曲的变形（$k_s\Delta d+k_b{\Delta }^{2}d=0$，见第9章），以及用于孔洞填充的平滑补片（${\Delta }^{2}x=0$，见第8章）。

4.4 总结与扩展阅读（Summary and Further Reading）

在本章中，我们介绍了三种关联紧密但各有区别的二维流形曲面与三角形网格平滑方法：流形调和函数为傅里叶变换在曲面网格上的推广提供了优雅的思路，但计算成本过高，难以适用于大多数应用；扩散流及高阶拉普拉斯流易于实现，是去除高频噪声的高效工具；表面光顺能生成尽可能平滑的曲面，且这些曲面正是其对应平滑流的极限曲面。

本章的讨论限于各向同性和线性平滑技术，这类技术易于理解且能满足大多数场景的需求。对于其他技术，读者可参考下文提及的更复杂方法。

各向异性扩散流（Anisotropic Diffusion Flow）

前文讨论的扩散流属于各向同性平滑方法，因为它会沿所有方向均匀扩散高频噪声。但该过程不可避免地会模糊尖锐边缘等几何特征。与之相反，各向异性扩散通过调整扩散方向来保留特征——平滑仅沿特征方向进行，而非跨特征方向。为此，需在各向同性拉普拉斯算子$\Delta f=\text{div}\nabla f$的基础上引入依赖数据的扩散张量$D(x)$，得到各向异性扩散流方程$\partial f/\partial t=\text{div}(D\nabla f)$[Perona and Malik 90]。各向异性表面平滑的相关示例可参考[Bajaj and Xu 03, Clarenz et al. 00, Desbrun et al. 00, Hildebrandt and Polthier 04]。

双边滤波（Bilateral Filtering）

图像的双边滤波[Tomasi and Manduchi 98]通过同时考虑图像域（传统滤波的处理对象）和值域（颜色值）来保留特征：每个像素是其空间邻域内颜色值相近像素的加权平均。[Fleishman et al. 03, Jones et al. 03]将双边滤波应用于表面去噪，他们同时考虑了空间距离（图像域）和法向量的局部变化（值域）。

非线性平滑（Nonlinear Smoothing）

在表面光顺中，我们用一阶和二阶偏导数替代了非线性内禀属性（如基本形式、主曲率），最终得到了求解光顺曲面的简单线性方程组。非线性平滑方法则直接求解真实的非线性最小化问题——虽然数值计算难度更大，但能生成质量更高的曲面，且对初始三角剖分或参数化的依赖更小[Moreton and Séquin 92]。例如，Schneider等人[Schneider and Kobbelt 01, Schneider and Kobbelt 00]求解非线性方程$\Delta H=0$；Bobenko与Schröder则最小化离散威尔莫流[Bobenko and Schrödder 05]；Eigensatz等人直接对离散平均曲率函数应用双边滤波，并重构出最接近滤波后曲率值的三角形网格[Eigensatz et al. 08]。