《Polygon Mesh Processing》1. 曲面的表示

原创已于 2025-12-09 14:37:10 修改 · 656 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#3d

于 2025-12-08 17:09:30 首次发布

在3维中，一个曲面有两种表示形式
1.参数方程
2.隐式方程

1.参数方程
是一个从2维参数到表示3D物体平面上点的空间坐标的3维参数的一个映射。

我们先设定 2 个独立的参数（通常用字母 u 和 v 表示，这就是 “二维参数” 的由来），这两个参数可以看作是一对 “控制坐标”。

把这两个参数代入参数方程后，就能计算出一组 3 个空间坐标值（对应三维空间的 (x,y,z) 轴）。
当让 u 和 v 在合理范围内取遍所有值时，计算出来的所有 ((x,y,z)) 坐标点，会刚好铺满三维物体的一个表面。

三维空间里的一个平面，就可以用参数方程
$z(u,v)),(u,v)∈D⊂R2\vec{r}(u,v)=\big(x(u,v),\;y(u,v),\;z(u,v)\big),\quad (u,v)\in D\subset\mathbb{R}^2$

eg
$e+fu))\vec{r}(u,v) = (a+bu, \; c+dv, \; e+fu))$
来表示，这里的 u 和 v 是两个参数，代入不同的 (u、v)，就能得到这个平面上的所有点。

可以不准确的将u,v理解为投影坐标点

r是一个向量，因为r代表的是一个1*3的向量，对应的是坐标(x,y,z).

2.隐式方程
是一个等号左边为表示3D物体平面上点的空间坐标的3维参数构成的标量表达式，等号右边为0的方程。
$F (x, y, z) = 0$
（满足该方程的所有(x, y, z)点，共同构成3D物体的表面）
eg:
$平面： 3 x - z + 2 = 0$
$球面：x^2 + y^2 + z^2 = R^2$

在实际中，根据实际的3种不同需求采用的不同的表示方法:

3种需求=指标
Evaluation：在对曲面进行采样的时候需要对其附加上一下除了空间信息之外的信息。例如在进行渲染的时候，除了几何体的空间坐标外，还需要其法向量信息。

Query：一个典型的空间查询是判断空间中的某个点是否在几何体的内部，另外还比如空间中某个点到某个曲面的距离。

Modification：一个曲面可以在几何上被修改（将一个平面卷起来），还可以在拓扑关系上被修改（把几张纸合并成一张更大的纸或者挖掉一张纸的一部分）。

曲面的定义和属性

书中对于曲面的定义如下：
an orientable continuous 2D manifold embedded in $R^{3}$
嵌入在 $R^{3}$ 中的可定向连续二维流形
也就是:
处于3维空间中的，方向连续的，不存在通过无限细小特征连接的的部分。

以下面两种情况为例，无限细小特征指的两个正方体表面相连接的部分。
也就是点接触和边接触，不视为面
在这里插入图片描述
这样两个正方体组成的组合体的外表面就不能称为一个面。

这样的组合体可以称之为：degenerate 3D solid(退化三维实体)

而把上面的两个组合体连接的部分变成下面这个样子之后，就不存在所谓的“通过无限细小特征相连接”的情况了.
在这里插入图片描述
这样组合体可以称之为：non-degenerate 3D solid(非退化三维实体
)

点边面的关系

在一个闭合连接网格内点(Vertex)，边(Edge)和面(Face)的数量存在下面的关系：

$V er t e x - E d g e + F a ce = 2 (1 - g)$

左边： $Vertex−Edge+Face\text{Vertex}-\text{Edge}+\text{Face}$ → 闭曲面的欧拉示性数（拓扑不变量，只和曲面的“洞数”有关，和具体形状无关）
右边： $2 (1 - g)$ → 用亏格 $g$ （洞数）表示的欧拉示性数

上面的式子中g表示的是曲面的亏格(genus)，
它的标准解释为：
若曲面中最多可画出n条闭合曲线同时不将曲面分开，则称该曲面亏格为n

而对于一般的闭合曲面来说亏格n就是几何体上洞眼的数目

球面（ $g = 0$ ）
若把球面分成“1个顶点、0条边、1个面”（简化情况）：
左边： $1 - 0 + 1 = 2$ ，右边： $2 (1 - 0) = 2$ → 等式成立
甜甜圈（环面， $g = 1$ ）
若把环面分成“4个顶点、4条边、2个面”：
左边： $4 - 4 + 2 = 2$ ，右边： $2 (1 - 1) = 0$ ？
（实际环面的欧拉示性数是0，正确拆分应为“2个顶点、4条边、2个面”： $2 - 4 + 2 = 0$ ，和 $2 (1 - 1) = 0$ 一致）
可以想象为将甜甜圈从中间横向片开，不是竖着切。这样的两个面构成了甜甜圈

对于一个三角形网格，基于上面的式子还能得到下面的关系：

三角形的数量大约是顶点数量的2倍 -> Face ≈ 2 * Vertex
边的数量大约是顶点数量的3倍 -> Edge ≈ 3 * Vertex
顶点邻边的数量平均是6
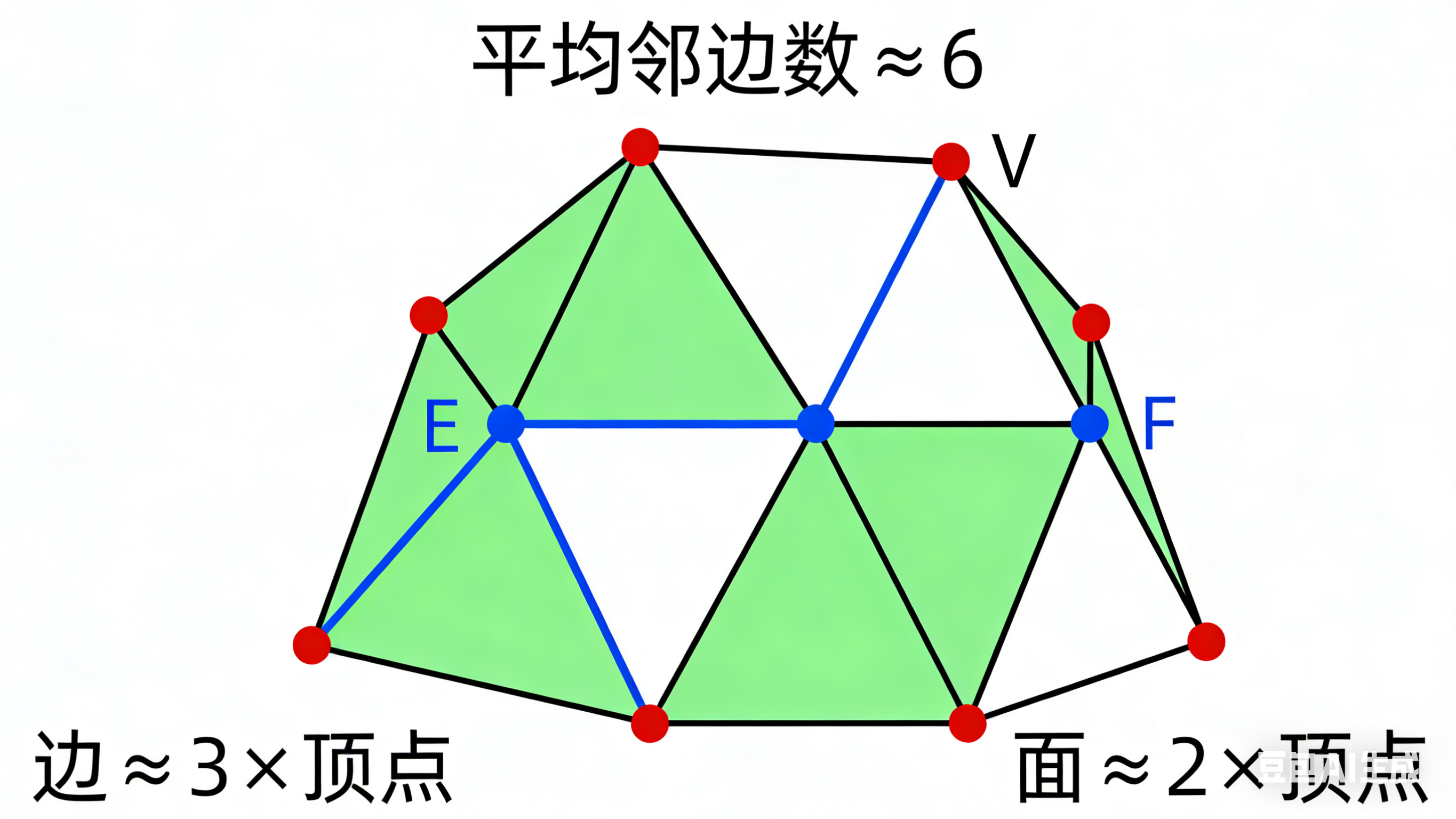
在这里插入图片描述
无需理解，这是公理。。

1.6 小结

第一章章我们探讨了不同数学几何表示方法的优缺点。
参数化与隐式表示这两大核心概念可谓各有所长：
1。参数化曲面能捕捉最细微的细节，采样便捷且支持直观修改，但处理距离查询和拓扑变更时需要进行大规模重构，这令人头疼；
隐式曲面虽然擅长处理拓扑变更和距离查询，但采
样与形状编辑并不直观，其几何细节分辨率还受体素尺寸的限制。

参考文章

[1] https://www.jianshu.com/p/47c350770ffe