《Polygon Mesh Processing》_第二章_网格数据结构

原创已于 2025-12-17 21:04:31 修改 · 957 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

于 2025-12-09 15:41:25 首次发布

2.0

重点掌握半边数据结构

选择网格数据结构的时候一般考虑下面两个因素：

两个因素

1.拓扑需求(Topological Requirements) ：需要表示什么样的网格？是二维流形，还是其它更复杂的网格？是单纯的三角形网格，或者其它任意的多边形网格？是需要给当前的网格附加上其它的网格？

使用三角形网格是因为，三个点就可以构成一个面，也就是三点共面。

2.算法需求(Algorithmic Requirements)：使用什么样的算法？是简单的渲染还是需要频繁的访问相邻的点边面？是静态网格还是动态网格？对于网格是否需要附加一些其它的属性？对内存的消耗是否特别在意？

评估一个数据结构的好坏有下面几个标准：

1.建立数据结构所需要预处理的时间
2.查询操作的响应时间
3.执行某项具体操作的时间
4.内存消耗和冗余

以下为四种数据结构

Faced-Based Data Structures (面基本数据结构)

这种数据结构最直观的优点是简单，这种数据结构由网格所有面的集合构成，而对于每一个面则使用组成面多边形的的点来表示。
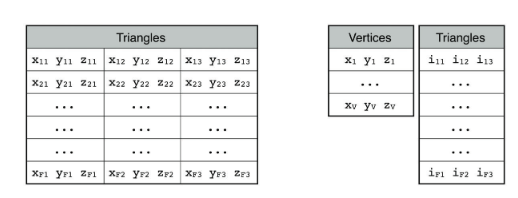
左边改进前右边改进后
以三角形网格为例，假设使用32位的单精度浮点数来表示坐标则，那么使用顶点的数据来表示一个三角形则需要36个字节
(3 vertex * 3 dimension * 4 byte = 36 byte)。
3个顶点，每个点x,y,z三个坐标，每个坐标4个字节(32位单精度浮点数)

通过上一部分的学习的公理可知任一顶点的邻边的平均数量为6，
即在这种数据结构中一个顶点平均会被存储6次，所以可以估算使用这种数据结构平均每一个顶点要使用72个字节(3 dimension * 4 byte * 6 time = 72 byte)

可以发现，一个顶点的数据被多次存储，一种可以改进这种空间冗余的方法是，使用数组来存储所有的顶点数据，而对于每一个三角形面只需要存储组成其的三个顶点的索引号即可。

即由两部分组成
要将给定的表格分成两个行数不一样的表格，可以按照以下步骤操作。假设需要将顶点数据和三角形数据分开：

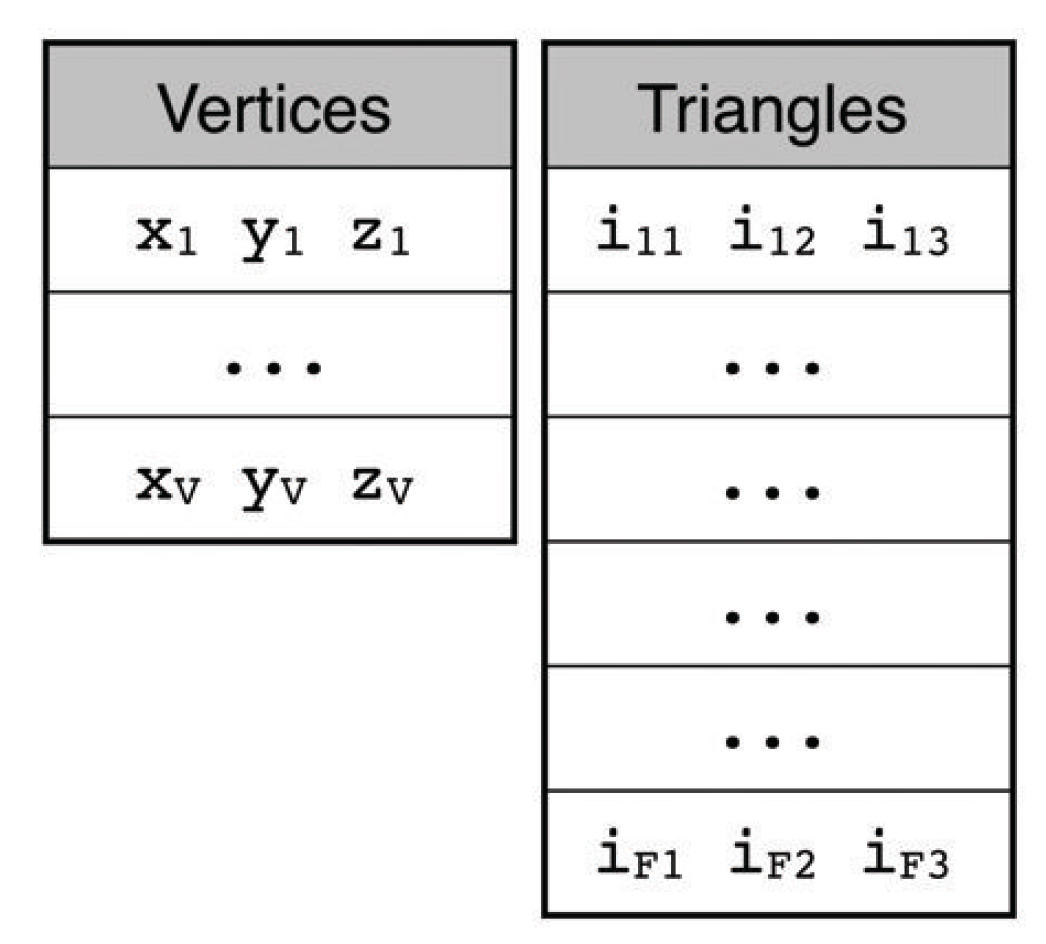
在这里插入图片描述
OFF OBJ VRML使用这种格式
这种数据结构的缺陷是:它缺少显式的连通性信息

Edge-Based Data Structures (基于边的数据结构)

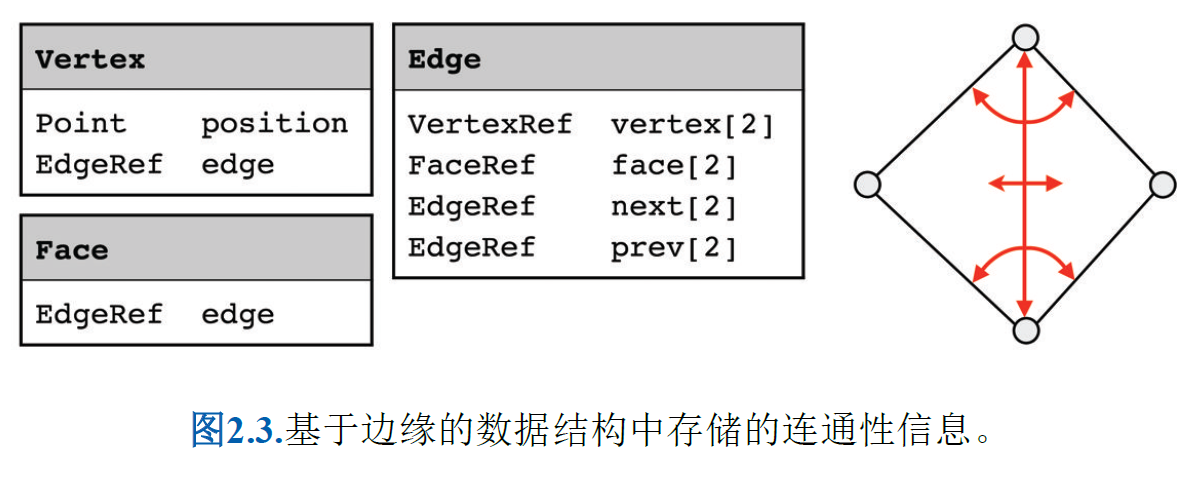
在这里插入图片描述
虽然基于边的数据结构能够表示任意多边形网格，但在遍历单环时仍
需区分情况（中心顶点是边的第一个顶点还是第二个顶点?)。这一问题
最终由半边数据结构解决。

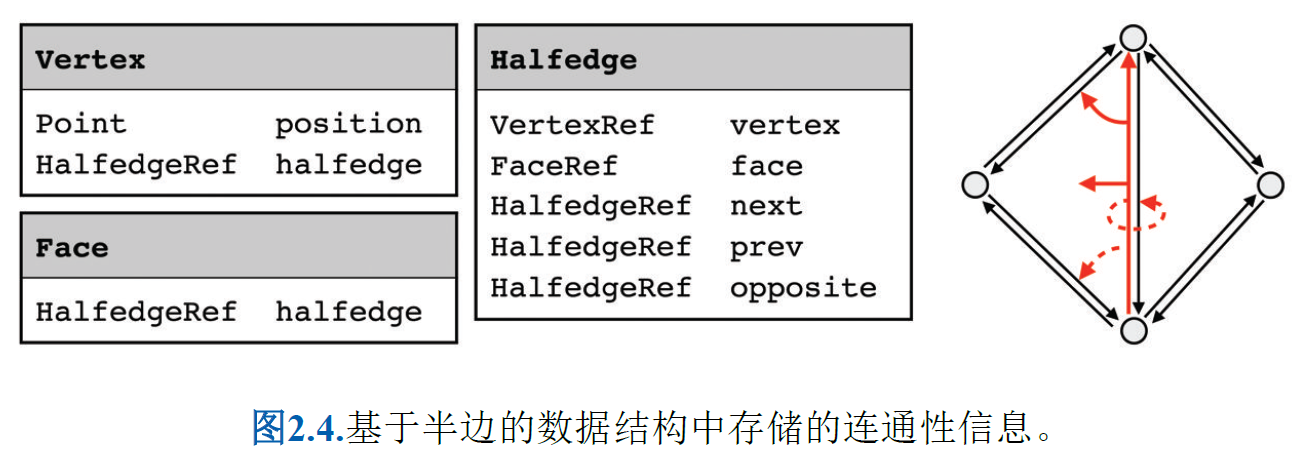
Halfedge-Based Data Structure (半边结构)

半边数据结构通过将每条无向边拆分为两条有向半边，
在半边数据结构中，半边沿每个面和边界始终按逆时针方向排列。因
此，每个边界可视为具有潜在高度的空面。由此，每条半边对应一个独特
的顶点（即面内非共享顶点），从而可按顶点存储纹理坐标或法线等属
性。
注意 Ponit，HaledegRef，VertexRef ，FaceRef是类名
在这里插入图片描述

#include <vector>
#include <cstdint>
#include <glm/glm.hpp>  // 用于存储顶点位置（可替换为自定义vec3）

// 前置声明（解决类之间的循环引用）
struct Halfedge;
struct Vertex;
struct Face;

// 半边类（核心数据结构）
struct Halfedge {
    uint32_t vertex_idx;  // 指向的顶点索引（关联Vertex数组）
    uint32_t face_idx;    // 相邻的面索引（关联Face数组，边界半边设为UINT32_MAX表示空）
    uint32_t next_idx;    // 下一条半边索引（关联Halfedge数组）
    uint32_t prev_idx;    // 前一条半边索引（关联Halfedge数组）
    uint32_t opposite_idx;// 对向半边索引（关联Halfedge数组）

    // 构造函数（默认初始化）
    Halfedge() : vertex_idx(UINT32_MAX), face_idx(UINT32_MAX),
                 next_idx(UINT32_MAX), prev_idx(UINT32_MAX),
                 opposite_idx(UINT32_MAX) {}
};

// 顶点类
struct Vertex {
    glm::vec3 position;       // 顶点3D位置
    uint32_t outgoing_halfedge;// 从该顶点出发的任意一条半边索引（用于遍历邻域）

    Vertex(const glm::vec3& pos = glm::vec3(0.0f)) 
        : position(pos), outgoing_halfedge(UINT32_MAX) {}
};

// 面类
struct Face {
    uint32_t first_halfedge;  // 面的第一条半边索引（用于遍历面的所有半边）

    Face() : first_halfedge(UINT32_MAX) {}
};

// 网格类（管理所有元素的容器）
class PolygonMesh {
public:
    std::vector<Vertex> vertices;    // 顶点数组
    std::vector<Face> faces;        // 面数组
    std::vector<Halfedge> halfedges;// 半边数组

    // 初始化示例：构建1个四边形面 + 边界的半边结构
    void initExampleMesh() {
        // 1. 初始化顶点（V0-V3，假设四边形顶点位置）
        vertices.emplace_back(glm::vec3(0.0f, 0.0f, 0.0f));// V0
        vertices.emplace_back(glm::vec3(1.0f, 0.0f, 0.0f));// V1
        vertices.emplace_back(glm::vec3(1.0f, 1.0f, 0.0f));// V2
        vertices.emplace_back(glm::vec3(0.0f, 1.0f, 0.0f));// V3

        // 2. 初始化面（1个内部面F0）
        faces.emplace_back();
        faces[0].first_halfedge = 0;  // F0的第一条半边是H0

        // 3. 初始化半边（H0-H7，对应之前的拓扑关系）
        halfedges.resize(8);

        // 内部半边 H0-H3（关联F0）
        halfedges[0] = {1, 0, 1, 3, 4};// H0: V1, F0, next=H1, prev=H3, opposite=H4
        halfedges[1] = {2, 0, 2, 0, 5};// H1: V2, F0, next=H2, prev=H0, opposite=H5
        halfedges[2] = {3, 0, 3, 1, 6};// H2: V3, F0, next=H3, prev=H1, opposite=H6
        halfedges[3] = {0, 0, 0, 2, 7};// H3: V0, F0, next=H0, prev=H2, opposite=H7

        // 边界半边 H4-H7（无关联面，face_idx=UINT32_MAX）
        halfedges[4] = {0, UINT32_MAX, 5, 7, 0};// H4: V0, 空面, next=H5, prev=H7, opposite=H0
        halfedges[5] = {3, UINT32_MAX, 6, 4, 1};// H5: V3, 空面, next=H6, prev=H4, opposite=H1
        halfedges[6] = {2, UINT32_MAX, 7, 5, 2};// H6: V2, 空面, next=H7, prev=H5, opposite=H2
        halfedges[7] = {1, UINT32_MAX, 4, 6, 3};// H7: V1, 空面, next=H4, prev=H6, opposite=H3

        // 4. 初始化顶点的出边半边（用于快速遍历）
        vertices[0].outgoing_halfedge = 4;  // V0的出边是H4（V0→V3）
        vertices[1].outgoing_halfedge = 0;  // V1的出边是H0（V1→V2）
        vertices[2].outgoing_halfedge = 1;  // V2的出边是H1（V2→V3）
        vertices[3].outgoing_halfedge = 2;  // V3的出边是H2（V3→V0）
    }

    // 辅助函数：判断半边是否为边界半边
    bool isBoundaryHalfedge(uint32_t he_idx) const {
        return halfedges[he_idx].face_idx == UINT32_MAX;
    }
};

// 使用示例
int main() {
    PolygonMesh mesh;
    mesh.initExampleMesh();

    // 验证H0的对向半边是否为H4
    Halfedge h0 = mesh.halfedges[0];
    Halfedge h4 = mesh.halfedges[h0.opposite_idx];
    printf("H0的对向半边指向顶点索引：%u（预期0）\n", h4.vertex_idx);
    printf("H4是否为边界半边：%s（预期true）\n", mesh.isBoundaryHalfedge(4) ? "true" : "false");

    return 0;
}

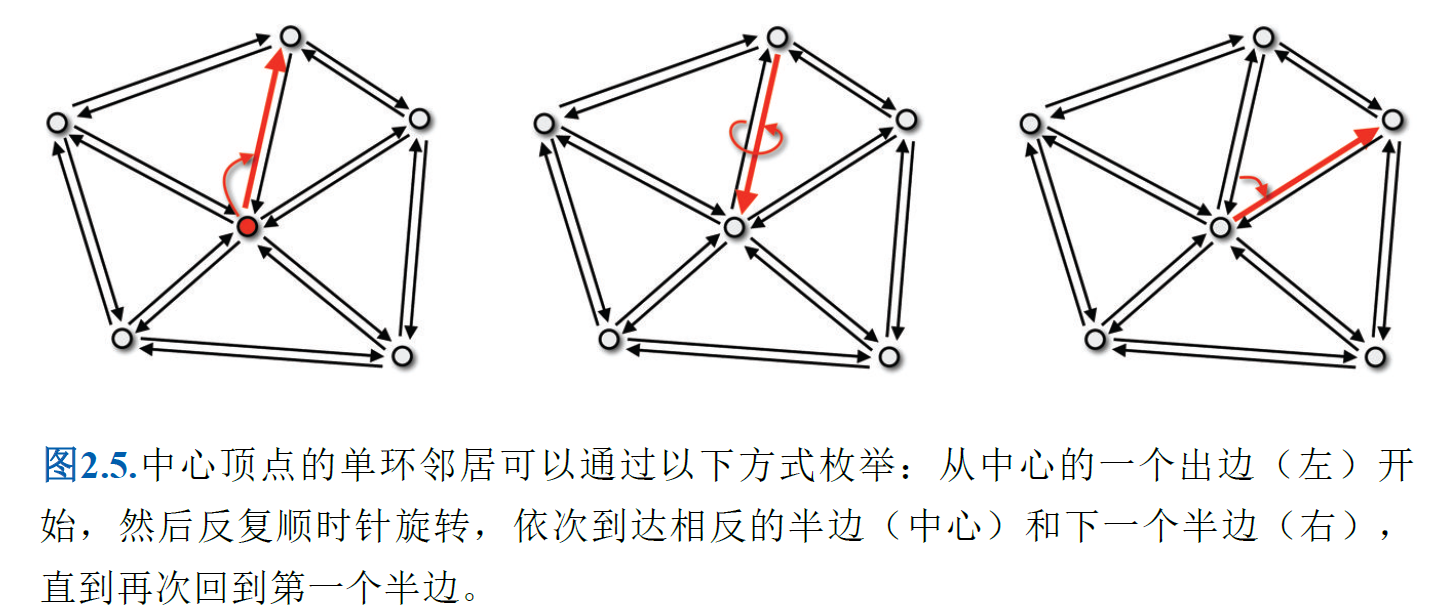
半边数据结构使我们能够枚举每个元素（即顶点、边、半边或面）的所有相邻元素。特别是，现在可以枚举给定顶点的一环邻域，而无需区分大小写

// 功能：枚举中心顶点的所有一环邻域顶点，并对每个邻域顶点执行自定义处理函数
// 参数：center - 中心顶点的引用；func - 处理邻域顶点的自定义函数（输入为顶点引用）
void enumerate_one_ring(VertexRef center, Function func) {
    // 1. 获取中心顶点的出半边（半边结构中，每个顶点关联一个"出"方向的半边作为遍历起点）
    HalfedgeRef h = outgoing_halfedge(center);
    
    // 2. 记录遍历终止标记（回到起始半边时停止循环）
    HalfedgeRef hstop = h;
    
    // 3. 循环遍历所有一环邻域（do-while确保至少执行一次，适配单邻边场景）
    do {
        // 4. 获取当前半边的目标顶点（即中心顶点的一个邻域顶点）
        VertexRef neighbor_vertex = vertex(h);
        // 5. 对邻域顶点执行自定义逻辑
        func(neighbor_vertex);
        // 6. 迭代到下一个邻域对应的出半边：
        //    - opposite_halfedge(h)：取当前半边的对边（邻域顶点的入半边）
        //    - next_halfedge(...)：取对边的下一条边（回到中心顶点的下一个出半边）
        h = next_halfedge(opposite_halfedge(h));
    } while (h != hstop); // 7. 回到起始半边，遍历完成，终止循环
}