Netgen自用

Nentgen v6.2.2505
发布于 jul 12 2025 (jul是7月)

Joachim Schöberl编写的交互式教程
教程1 有限元法的交互式入门
教程2 NGS-Py 有限元工具
讲义  下载地址
NGSolve Jupyter笔记本

使用jupyter-notebook进行

由于netgen可以基于web端进行渲染，所以使用jupyterbook可以很好的看见代码的运行结果

pip install notebook
pip install ipywidgets==8.1.1
pip install jupyterlab_widgets
pip install webgui_jupyter_widgets

Netgen/NGSolve 的对象名称为OCCGeometry，OCCGeometry 继承自 NetgenGeometry，代表一个 OpenCascade 几何体。
全局网格参数
maxh: 全局最大网格尺寸（默认 1e10），越小越细。
grading: 网格尺寸变化的渐变系数，越小表示变化更平缓（默认 0.3）。
meshsizefilename: 可提供一个文件来设定局部网格尺寸，文件格式是“点数 + 每个点的坐标和尺寸”，然后是“线段数 + 每个线段两端点与尺寸”。
segmentsperedge: 每条边至少划分多少段（默认 1）。
quad_dominated: 是否让表面尽量使用四边形单元（默认 False）。
blockfill, filldist: 是否使用 block fill 快速铺充、及其距离（默认 True 和 0.1）。
delaunay, delaunay2d: 3D/2D 是否使用 Delaunay 网格生成。

1.1 First NGSolve example

1.使用netgen创建一个几何体

# 检测是否成功安装了netgen
python3 -c "import ngsolve; print(ngsolve.__version__)"

from ngsolve import *
from ngsolve.webgui import Draw
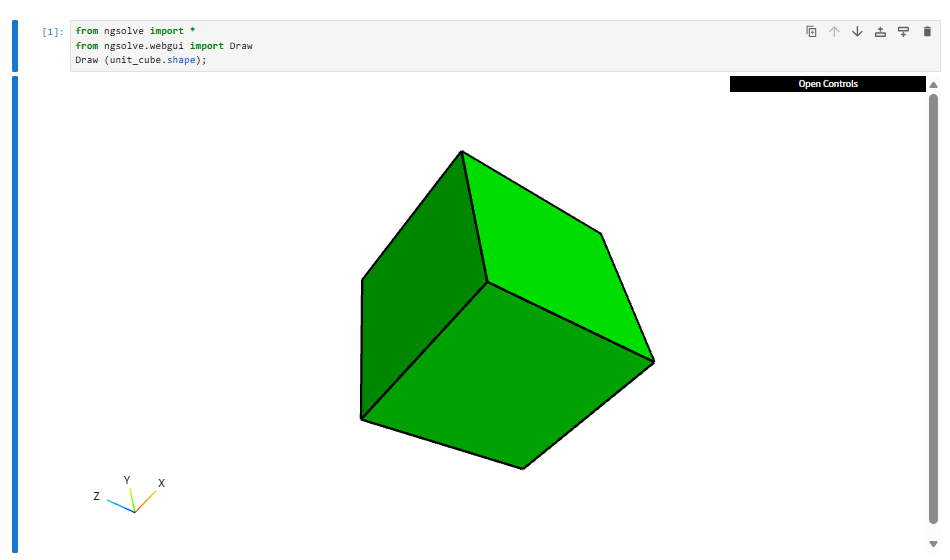
Draw (unit_cube.shape);  
#unit_cube来自 netgen.occ 模块，是一个预定义的 OCCGeometry（单位立方体）。

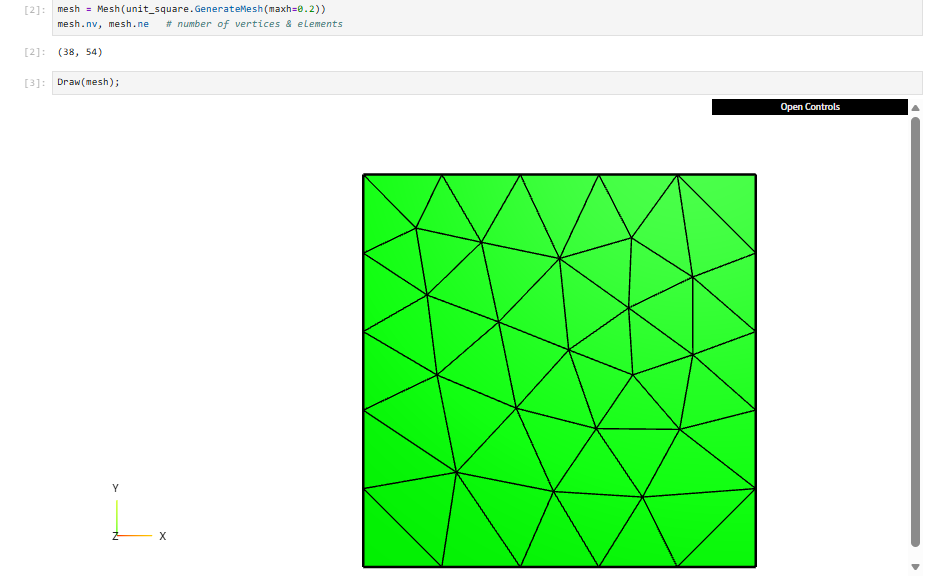
mesh = Mesh(unit_square.GenerateMesh(maxh=0.2))   
#nit_square 是 netgen.occ 里预先定义好的 1×1 平面几何。
#GenerateMesh(maxh=0.2) 调用 Netgen 的表面网格生成器来对该几何进行剖分，其中 maxh=0.2 指定网格的最大单元尺寸（越小越细）。

mesh.nv, mesh.ne   # number of vertices & elements
#查询网格的 nv（number of vertices）和 ne（number of elements），查看网格规模的操作，会输出节点数和单元数。
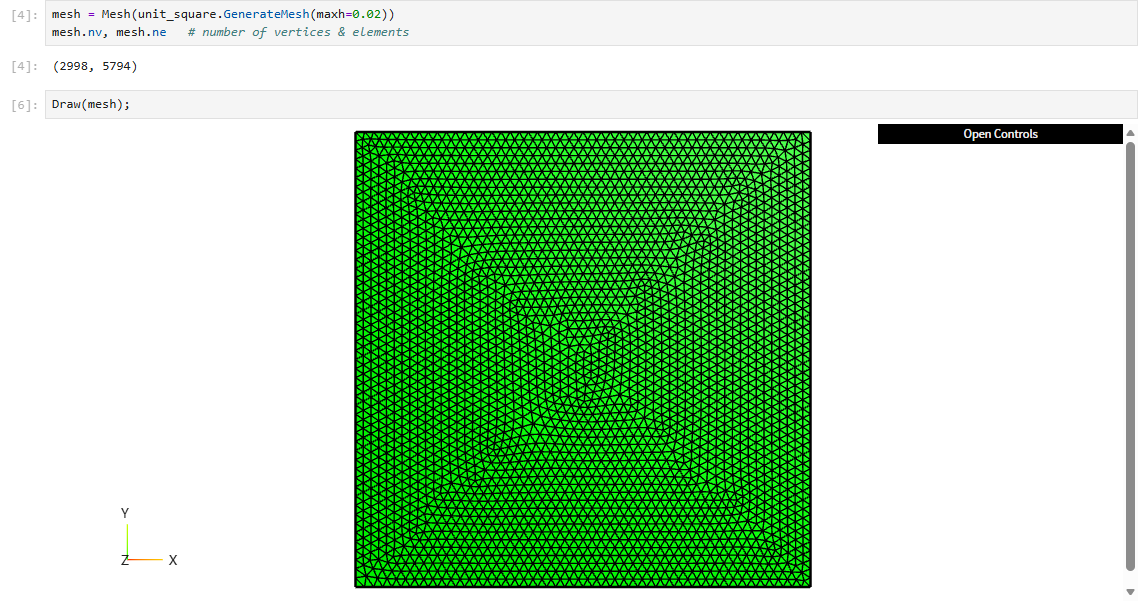
Draw(mesh);

$$\begin{array}{r}\begin{array}{rlrl}-\Delta u& =f& & \text{ 在单位正方形内},\\ u& =0& & \text{ 在边界底部和右侧},\\ \frac{\partial u}{\partial n}& =0& & \text{ 在其余边界部分}.\end{array}\end{array}$$

3. 声明一个有限元空间：

fes = H1(mesh, order=2, dirichlet="bottom|right")   
#创建 H¹ 空间（一阶 Sobolev 空间），用于求解二阶 PDE（如泊松方程）。
#order=2：使用 2 次多项式基函数（分段二次）。
#dirichlet="bottom|right"：在底部和右侧边界上施加 Dirichlet 边界条件（u = 0），这些边界上的自由度会被约束。

fes.ndof  #这个空间中的未知数数量  返回该有限元空间的自由度（DOF）数量，即待求解的未知数个数。

参考文章：
[1]开源科学工程技术软件介绍45 – 多物理有限元软件Netgen/NGSolve