《Polygon Mesh Processing》_第三章_微分几何学(未完成)

3.0 写在前面

  第三章核心价值在于搭建 “连续微分几何” 与 “离散 3D 网格” 之间的桥梁—— 它把曲线、曲面的经典微分几何理论（如曲率、第一 / 第二基本型、内蕴几何），落地为可计算的离散形式（如离散拉普拉斯算子、离散曲率），是 3D 网格处理领域的 “理论基础 + 工程工具集”。

3.1 曲线

3.1.1 弧长

  计算弧长就是计算函数的积分
$$s=s(u)={\int }_a^u\Vert x^{\prime }(t)\Vert dt.\text{\hspace{1em}(3.1)}$$

3.1.2 曲率

  假设一条正则曲线是按弧长参数化的，那么我们可以将点 x(s)处的曲率定义为
$$\kappa (s):=\Vert x^{\prime \prime }(s)\Vert$$

对于任意一条具有参数化 u 的正则曲线，我们可以利用根据弧长 ( s(u) ) 进行的重新参数化来定义曲率。
直观地说，曲率用于衡量曲线偏离直线的程度。
换句话说，曲率将曲线切向量的导数与曲线法向量联系起来，并且还可以通过关系式 来定义。
$$x^{\prime \prime }(s)=\kappa (s)\vec{n}(s)$$

需要注意的是，在这个定义中，曲率是有符号的，因此当法向量的方向反转时，曲率的符号也会改变。

不难看出，直线的曲率为零，而任何处处曲率为零的曲线必定是线段。具有恒定曲率的平面曲线是圆弧。曲率也可以定义为密切圆半径的倒数。密切圆在曲线的点 ( x(u) ) 处对曲线进行局部最佳逼近，其构造方法如下：设 ( c(u_{-}, u, u_{+}) ) 是经过三个曲线上的点 ( x(u_{-}) )、( x(u) ) 和 ( x(u_{+}) )（其中 ( u_{-} < u < u_{+} )）的圆。那么，在点 ( x(u) ) 处的密切圆 ( c(u) ) 定义为
$$c=\underset{u_{-},u_{+}\to u}{\lim }c(u_{-},u,u_{+})$$
密切圆的半径为 $(1/\kappa (u))$，并且在点 x(u) 处与曲线相切。

3.2 面

长度和曲率是曲线的欧几里得不变量，即它们在刚体运动下保持不变。现在我们将研究嵌入在${\mathbb{R}}^3$中的光滑曲面的类似度量和曲率性质 。这些特性通过参数化表面表示法更易定义，下文将对此进行说明。随后，将从该参数化表示法中推导出度量特性。这些微分特性的三角网格离散化方法将在3.3节中阐述。

3.2.1 曲面的参数

2. 完整参数化球体方程：
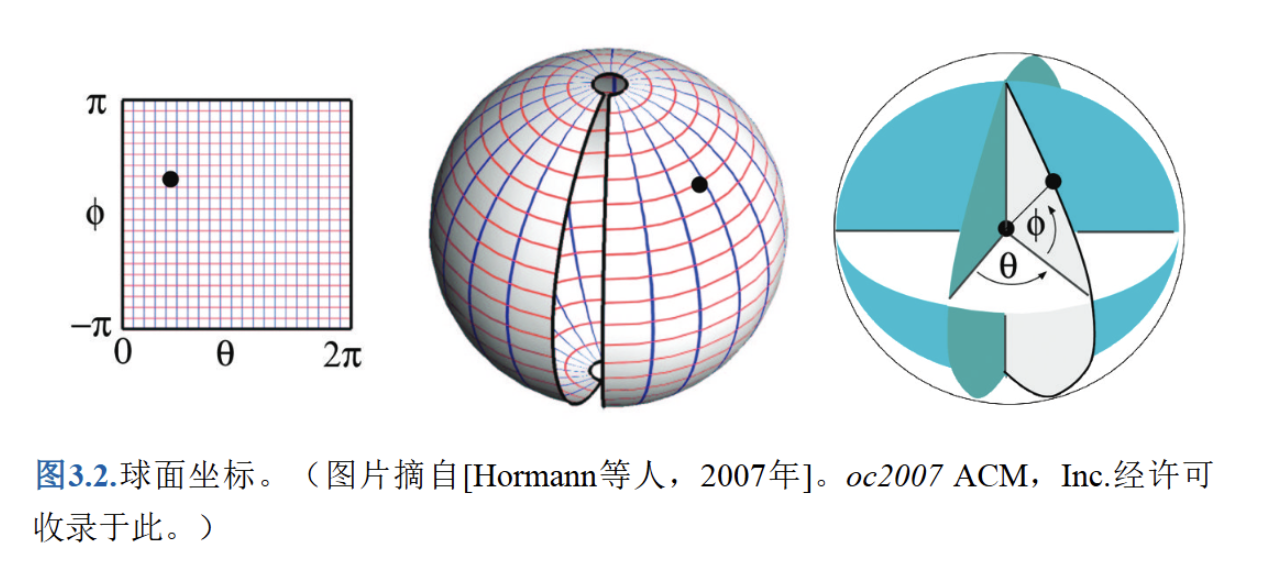
   三维空间中的 (x, y, z) 坐标和球坐标参数 (θ, φ) 的映射方程（参数化球体方程）为：
   $$x(\theta ,\varphi )=\left(\begin{array}{c}x(\theta ,\varphi )\\ y(\theta ,\varphi )\\ z(\theta ,\varphi )\end{array}\right)=\left(\begin{array}{c}R\cos \theta \cos \varphi \\ R\sin \theta \cos \varphi \\ R\sin \varphi \end{array}\right)$$
   其中：

• θ ∈ [0, 2π]，为方位角（绕 z 轴旋转的角度）；
• φ ∈ [-π/2, π/2]，为极角（与 z 轴的夹角）；
• R 为球体的半径。