2021-02-06

滑模控制

滑模控制（变结构控制）起源于继电器控制和 Bang-Bang 控制，它与常规控制的区别在于控制的不连续性。滑模控制是变结构控制的一 个分支。它是一种非线性控制，通过切换函数来实现，根据系统状态偏离滑模的程度来切换控制器的结构（控制律或控制器参数），从而使系统按照滑模规定的规律运行的控制方法。
控制性能：滑模控制对非线性系统特别是离散系统有良好的控制性能，
可应用性：对多输入多输出系统可应用性极强。
鲁棒性：当系统处于滑动模型，对被控对象的模型误差、对象参数的变化以及外部干扰有极佳的不敏感性。
抖振：当状态轨迹到达滑动模态面后，难以严格沿着滑动模态面向平衡点滑动，而是在其两侧来回穿越地趋近平衡点，从而产生抖振

滑模控制的原理
设存在一个系统

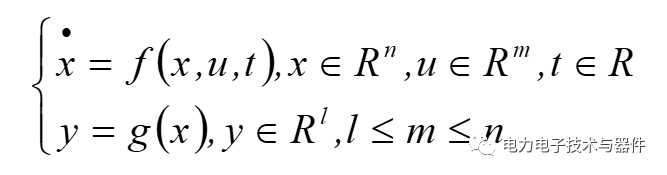
其中，x,u,y 分别表示系统的状态变量、输入变量、输出变量， n,m,l 分别表示系统的状态变量、输入变量、输出变量的维数， R 表示实数域。
首先需要确定切换函数向量：

具有的维数一般情况下等于控制的维数。
并且寻求变结构控制：

这里的变结构体现在当u+(x)≠u-(x)，使得以下三个条件成立：
（1）滑动模态存在，即满足：

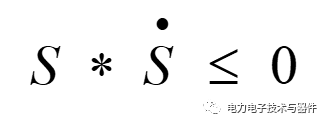
（2）到达条件，切换面Si(x)=0以外的相轨迹将于有限时间内到达切换面
（3）切换面是滑动模态区，且滑模运动渐近稳定,动态品质良好
满足以上三个条件便可以做滑模变结构控制。
04
滑模控制设计步骤
设计滑模变结构控制器的基本步骤包含两个相对独立的部分
（1）选取设计切换函数S(x)，使之所确定的滑动模态渐进稳定（参照李雅普诺夫稳定性）且具有良好的动态品质
a.线性系统：一般设

b.非线性系统一般可使用三种方法，分别是终端滑模，积分滑模以及分段线性滑模
（2）求取控制律u=u±(x)，从而使到达条件满足时，在切换面上形成滑动模态区。
方法1：采取滑动模态存在条件

求得控制律的一个不等式，需要在满足此不等式的条件下选择合适的控制律。
方法2：采用趋近律方法，可直接求取等式型控制律
以下为几种常见的趋近律