线性控制系统的Nyquist频域稳定分析方法

目录

频域分析法

典型环节的幅相频率特性曲线

1.二阶震荡环节()

2.惯性环节

奈奎斯特稳定判据

1.柯西幅角原理：

2.线性控制系统

判断控制系统稳定的具体步骤

频域分析法

典型输入信号：正弦信号

研究的是稳态情况下，正弦响应的幅值和相角随频率的变化规律，不考虑暂态响应。

由开环频率特性研究闭环稳定性及性能。(避免求解闭环特征方程的根)幅相频率特性（Nyquist）

典型环节的幅相频率特性曲线

 假设传递函数为，则可利用matlab进行Nyquist曲线绘制，代码如下：

num = [4];
den = [1 2 4];
sys = tf(num,den)
nyquist(sys)

1.二阶震荡环节()

幅频特性：                 相频特性：

谐振频率：                        谐振峰值：

2.惯性环节

幅频特性：，相频特性：

注：根据不同的传递函数，可以直接使用matlab进行Nyquist曲线绘制。

奈奎斯特稳定判据

用于分析单变量系统的稳定性。

稳定判据：P-Z=N；P：s右半平面开环传递函数极点个数，Z：s右半平面闭环传递函数极点个数，N：Nyquist曲线绕（-1，j0）点的圈数。

1.柯西幅角原理：

奈奎斯特稳定判据的理论基础。

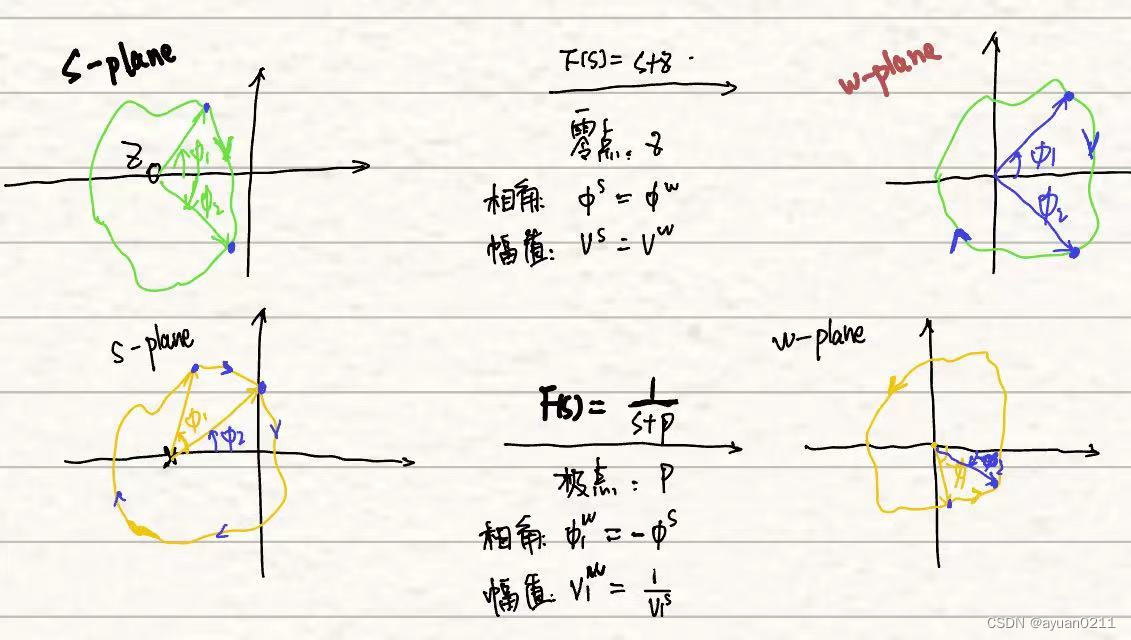
如图所示：

在复平面s内，顺时针画一条闭合曲线A，B曲线是A通过F(s)后，在w平面上的映射。

A曲线每包含F(s)的零点，B曲线就绕（0,0）点顺时针一圈；

A曲线每包含F(s)的极点，B曲线就绕（0,0）点逆时针一圈。

B曲线逆时针绕（0,0）点的圈数 = 极点和零点的个数差。

2.线性控制系统

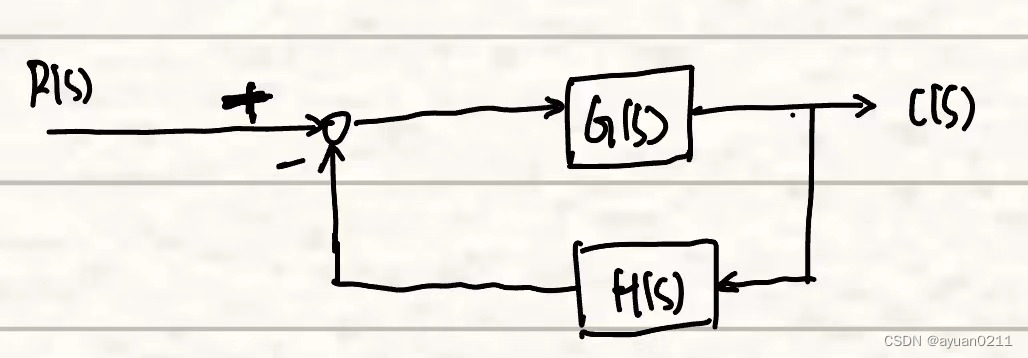
系统开环传递函数为GH：其中G可以表示为：    ，H可以表示为：，则：；

系统闭环传递函数为；

构造映射函数为:;

由上式可得到结论：系统开环传递函数的极点与映射函数F(s)的极点相同，系统闭环传递函数的极点与映射函数F(s)的零点相同。

对于线性控制系统来说，曲线A为复平面s的右半平面，即Nyquist Contour。

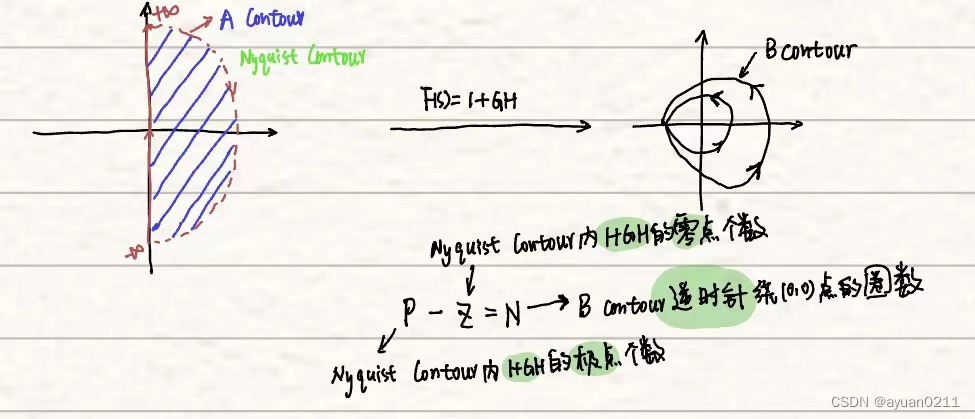
结合上面结论：P就是开环传递函数的极点，Z就是闭环传递函数的极点。

由于是线性系统，F(s)=1+GH，即向左平移一个单位，由此，将F(s)转换为GH，即为线性系统GH的Nyquist曲线。

那么：N则变换为B Contour逆时针绕（-1，j0）点的圈数。

由此可推导出：Nyquist稳定判据：P-Z=N；

                        P：s右半平面开环传递函数极点个数，

                        Z：s右半平面闭环传递函数极点个数，

                        N：Nyquist曲线绕（-1，j0）点的圈数。

由于系统稳定，则闭环传递函数在s右半平面的极点个数为0，即Z=0，则P=N。

判断控制系统稳定的具体步骤

step1：根据给出的开环传递函数得到P。

step2：通过MATLAB绘制Nyquist曲线，查看Nyquist曲线包含（-1，j0）点的圈数N，看包围的圈数，根据Nyquist曲线的方向从实轴交点开始算起即可。

例：

step3：逆时针，N为正，上图即为N=2；顺时针即为负。

step4：判断是否满足等式P-Z=N，若满足则系统稳定，若不满足则系统不稳定。

参考：

https://www.bilibili.com/video/BV1F34y1h7so?p=41&vd_source=ed5408ad8775097c07913f4b4155ca01

【自动控制原理】13_奈奎斯特稳定性判据_Nyquist Stability Criterion_Part 1_哔哩哔哩_bilibili