基于证据理论的WSN覆盖优化

基于数据融合与证据理论的无线传感器网络节点部署算法

摘要

近年来，无线传感器网络得到了广泛的研究和发展。节点部署问题是一个具有连续离散变量的多维非线性优化问题。为了提高无线传感器网络的覆盖率，提出了一种基于证据理论的网络覆盖算法。该算法计算无线传感器节点的运动方向，将无线传感器节点移动到低感知概率区域，从而改善网络覆盖效果，减少无线传感器节点的移动距离，延长无线传感器网络的服务时间。仿真结果表明，该算法能够有效提高监测区域的覆盖效果，并减少节点的移动距离。

关键词 节点部署算法 · 数据融合 · 证据理论 · 无线传感器网络 · 覆盖优化

1 引言

无线通信技术、传感器技术和智能信息网络技术迅速发展。集感知、存储和通信能力于一体的无线传感器网络在军事、国防、建筑监测、环境监测、智能家居、空间探索等领域得到了越来越广泛的应用[1–4]。

海洋与海洋经济的发展是人类生存和社会发展的唯一现实途径。随着各国对海洋资源的日益关注以及海洋经济热潮的兴起，各国已纷纷启动并制定了海洋资源开发战略。

无线传感器网络（WSN）的应用已逐步扩展到水下应用环境，成为无线传感器网络系统研究中的一个重要领域。水下无线传感器网络（UWSN）具有高精度、实时和时空连续性等特点，已成为新的研究热点[5–8]。

水下无线传感器网络（UWSNs）可将具有短距离无线通信和有限能量的水下无线传感器节点散布到指定探测区域，同时利用水下无线传感器网络节点的自组织功能构建水下无线传感器网络[9–12]。

水下无线传感器网络中的节点利用多种无线传感器的感知功能收集数据信息，并监测水下无线传感器网络中待测区域的各种被监测目标的分布情况。经过水下无线传感器网络节点的数据处理和数据信息融合后，具备远距离通信功能的汇聚节点将获取数据信息，并以准确的无线方式将其传输至水面基站。然后，所获得的数据信息将通过附近无线基站或高空卫星等无线中继节点传送到数据信息中心[13–16]。

根据水下无线传感器网络节点的不同类型，可以获得不同的数据信息，从而收集海洋中的数据信息。它可以监测水下环境，发挥防灾功能，并辅助水下导航设备进行水下导航与定位。此外，还可用于海洋资源勘探以及对水下目标的探测、跟踪和定位。

由于水下环境的特性，水下无线传感器网络与传统的无线传感器网络有很大不同。传统无线传感器网络中的许多技术，如节点部署策略、覆盖控制技术、通信技术、节点定位技术和路由技术，无法直接应用于水下传感器网络。为了使水下传感器网络能够完成目标监测和信息获取任务，传感器节点必须更有效地覆盖监测区域。

水下无线传感器网络节点的部署会影响无线传感器网络的成本和性能[21–24]。

水下无线传感器网络节点的合理部署方案可以提升无线传感器网络使用效果，从而降低成本。因此，在水下无线传感器网络中应采用何种节点部署策略和覆盖控制方法是一个非常重要的问题，这直接关系到无线传感器网络中节点能量、通信带宽、计算处理能力等有限资源的最优分配，同时也影响水下无线传感器网络的感知、监测、通信等服务质量目标。由于传感器网络所处位置复杂多变，特别是水下环境也具有复杂性和多变性，单个传感器节点的性能会受到水下环境的限制，节点采集的数据可能在一定程度上偏离实际情况，从而影响整个传感器网络的感知服务质量。

因此，非常有必要采用多个传感节点的数据融合来保障感知服务质量[25–28]。

因此，本文将研究不同数据融合算法对水下传感器网络节点部署的影响，并提出一种具有较强理论意义和实际应用意义。本文其余部分组织如下：第2节介绍相关工作。第3节详细描述本文算法。第4节通过仿真与其他算法进行比较。第5节对全文进行总结。

2 相关工作

水下无线传感器网络是由水下声学无线通信技术和无线传感器网络技术结合而产生的。水下无线传感器网络可为海洋环境管理、海洋资源保护、海洋灾害监测、海洋工程、近海生产作业以及海洋军事活动提供技术装备和信息平台。因此，水下无线传感器网络受到世界各国政府各部门、工业界、学术界和科研机构的广泛关注[29–32]。

传感器节点的部署反映了传感器网络的成本和性能。良好的部署策略可以提高传感器网络的感知质量并降低成本。因此，水下无线传感器节点的部署策略和覆盖控制方法成为水下无线传感器网络中亟待解决的主要问题。它直接关系到节点能量、通信带宽和传感器网络计算处理能力等有限资源的最优分配，并影响水下传感器网络的感知、监测和通信等各种服务质量目标[33–36]。

由于传感器网络位置的复杂性和多样性，特别是水下环境的复杂性和多变性，单个传感节点的性能受到水下环境的限制，节点采集的数据可能与实际情况存在一些偏差，进而影响整个传感器网络的感知服务质量。因此，采用多个感知节点的数据融合来确保感知服务质量。水下传感器网络是传感器网络研究中的热点。由于水下传感器网络的研究方向和内容多样，其研究是一项艰巨而具有挑战性的任务[37–40]。

具有低能耗和短距离无线通信的水下无线传感器网络节点被部署到指定监测区域。基于水下无线传感器网络节点的自组织能力，构建了水下无线传感器网络。水下无线传感器网络中的无线传感器节点利用多种无线传感器实时监测并采集网络分布区域内的各种数据与信息。经过数据融合技术处理后，具备远距离无线通信能力的水下汇聚节点将实时被监测的数据和信息通过无线方式传输至水面基站，再通过近海基站或其他中继节点（如卫星）将实时数据和信息传送到信息中心。作为无线传感器网络在水下环境中的延伸，水下无线传感器网络具有与基本无线传感器网络架构相同的结构。但由于水下传感器网络的特殊应用环境，该领域仍面临诸多挑战[41–44]。

虚拟分子力算法假设移动传感器网络中节点之间的相互作用，这些作用力的合力构成了网络中传感器节点的监测区域，从而使传感器节点移动到相应位置以修复监测盲区，最大化网络的覆盖率[1]。

设计了一种基于虚拟力场算法的水下无线传感器网络算法，称为聚焦虚拟力场。提出了聚焦区域的概念。通过调节虚拟场节点的受力和参数，对被监测水体进行划分。该虚拟力场算法用较少的节点即可实现对水体的良好覆盖率，并保证主要区域的覆盖。此外，通过使用运动受限节点降低了系统成本[2]。

3 本文算法

基于虚拟力算法的节点部署方案通过无线传感器节点之间的位置关系进行计算，受无线传感器节点密度的影响较大。对于大量固定无线传感器节点的无线传感器网络，虚拟力算法可能无法突破固定无线传感器节点虚拟力的限制，难以达到全局优化的目标。基于证据理论的节点部署算法采用概率感知模型的移动方案，更符合实际情况。

3.1 识别框架

一组完整且互斥的元素称为识别框架，并用符号表示。待监测区域中任意一点的识别框架为Θ={H₀,H₁}，其中H₀表示“未被无线传感器节点感知”，而H₁表示“被无线传感器节点感知”。

3.2 证据理论

设m₁和m₂为同一识别框架上的基本概率分布函数Θ，其焦元分别为Aᵢ和Bⱼ，两个证据的合成公式为

$$
m_1 \oplus m_2(A) =
\begin{cases}
0 & \text{if } A = \varnothing \
\frac{\sum_{A_i \cap B_j = A} m_1(A_i)m_2(B_j)}{1 - K} & \text{if } A \neq \varnothing
\end{cases}
$$

在公式(1)中，$K = \sum_{A_i \cap B_j = \varnothing} m_1(A_i)m_2(B_j)$ 表示证据冲突的程度；⊕表示直和运算。

N个证据可以通过公式（2）传递

$$
m(A) = m_1 \oplus m_2 \oplus \cdots \oplus m_N(A)
$$

在公式(2)中，获得了多条证据的基本概率函数。

3.3 节点感知模型

节点感知模型是节点部署研究的基础。不同的应用场景需要构建不同的节点感知模型，感知模型的质量直接影响节点部署研究的准确性和正确性。在理论研究中，常用的节点感知模型主要有以下三种方式：

3.3.1 0–1感知模型

0–1感知模型是最简单且最常用的一种模型。在二维网络系统中，传感器的感知范围可被视为以传感节点为中心、半径为Rₛ的圆形区域。

假设感知节点的坐标为(xₛ, yₛ)，目标节点的坐标为(xₚ, yₚ)，d(S, P)表示感知节点S与目标节点P之间的欧几里得距离，即$d(S, P) = \sqrt{(x_S - x_P)^2 + (y_S - y_P)^2}$，C(S, P)表示感知节点S对目标节点P的感知概率。则0–1模型的数学形式如下：

$$
C(S, P) =
\begin{cases}
0 & \text{if } d(S, P) > R_S \
1 & \text{if } d(S, P) \leq R_S
\end{cases}
$$

在三维网络架构中，无线传感器的感知范围可被视为以传感节点为中心、半径为Rₛ的球形区域。假设感知节点的坐标为(xₛ, yₛ, zₛ)，目标节点的坐标为(xₚ, yₚ, zₚ)，d(S, P)表示感知节点与目标节点之间的欧几里得距离，即$d(S, P) = \sqrt{(x_S - x_P)^2 + (y_S - y_P)^2 + (z_S - z_P)^2}$，C(S, P)表示感知节点对目标节点的感知概率。则0–1模型的数学形式如公式(3)所示。

0–1模型相对简单，因此在研究网络覆盖控制问题时，0–1模型是最常见的。然而，它相对粗糙，因为它忽略了实际应用中的许多影响因素。有时得出的结论与实际情况相差甚远，其应用正逐渐减少。

3.3.2 概率感知模型

由于环境因素的影响以及信号在传输过程中的衰减，感知节点对目标节点的感知概率与两者之间距离的关系在实际应用中是一个渐变的过程。两者之间的距离越近，感知概率越大；反之则越小。在概率感知模型中，感知概率C(S, P)与它们之间的欧几里得距离d(S, P)之间的关系可以用以下公式描述：

$$
C(S, P) = e^{-d(S, P)}
$$

在公式(4)中，λ表示传感节点对目标节点的感知能力以及信号随距离的衰减程度。

由于概率感知模型能够更好地反映实际应用中的多种不确定因素，与0–1模型相比，能更准确地反映传感器节点的有效覆盖能力，因此概率感知模型在实际应用中也得到了越来越广泛的使用。

将三维监测区域离散化为L × W × H个小立方体。本文中，定义无线传感器节点j在小立方体i处感知到的事件为rᵢⱼ，P(Pᵢ, Sⱼ)是小立方体i被无线传感器节点j感知到的概率。

$$
P(P_i, S_j) =
\begin{cases}
0 & \text{if } d(P_i, S_j) \geq R_S + R_E \
\frac{e^{\frac{R_S + R_E - d(P_i, S_j)}{2R_E}} - 1}{e - 1} & \text{if } R_S - R_E < d(P_i, S_j) < R_S + R_E \
1 & \text{if } d(P_i, S_j) \leq R_S - R_E
\end{cases}
$$

在公式(5)中，d(Pᵢ, Sⱼ)表示小立方体i与无线传感器节点j之间的距离，Rₑ表示无线传感器节点的感知误差范围。

通过基于证据理论的感知概率融合，无线传感器网络对第i个像素的感知概率为

$$
P(P_i) = P(P_{i,1}) \oplus P(P_{i,2}) \oplus \cdots \oplus P(P_{i,N})
$$

3.4 网络覆盖模型

本文考虑待监测区域由L × W × H个小立方体组成，每个小立方体占据Δx × Δy × Δz。

第i个小立方体pᵢ被传感器网络发现的可能性为P(Pᵢ)。如果经计算P(Pᵢ) = 0，则该小立方体的中心点pᵢ未被传感器网络发现；如果经计算P(Pᵢ) = 1，则该小立方体的中心点Pᵢ被传感器网络发现。

如果第i个小立方体的中心点pᵢ被传感器网络检测到，则P_cov(Pᵢ) = 0；如果第i个小立方体的中心点Pᵢ被传感器网络检测到，则P_cov(Pᵢ) = 1。

用于衡量传感器网络覆盖效果的数学模型如下所示

$$
R_{cov} = \frac{A_{cov}}{A_{sum}} = \frac{\sum_{i=1}^{x}\sum_{j=1}^{y}\sum_{k=1}^{z} P_{cov}(P_i) \times \Delta x \times \Delta y \times \Delta z}{L \times W \times H \times \Delta x \times \Delta y \times \Delta z}
$$

3.5 节点运动模型

在待监测区域中，节点a定位后的坐标为(xₐ, yₐ, zₐ)；则节点a与节点b之间的欧几里得距离为

$$
d(S_a, S_b) = \sqrt{(x_a - x_b)^2 + (y_a - y_b)^2 + (z_a - z_b)^2}
$$

在网络运行过程中tₙ，当引力与斥力相等时，两节点之间的距离为dₙ。当d(Sₐ, S_b) < dₙ时，两节点之间的距离过近，斥力大于引力。当d(Sₐ, S_b) ≥ dₙ时，表示两节点之间的距离过远，引力大于斥力，此时引力起主导作用。

$$
d_n = \frac{2nR_S}{n + 1}
$$

在公式(10)中，n为正整数。

经过计算，节点a获得的坐标为(x̂ₐ, ŷₐ, ẑₐ)，节点b获得的坐标为(x̂_b, ŷ_b, ẑ_b)。

当 d(Sₐ, S_b) < dₙ

$$
x̂_a = x_a + \frac{ d_n - d(S_a, S_b) }{2d(S_a, S_b)}
$$

$$
ŷ_a = y_a + \frac{ d_n - d(S_a, S_b) }{2d(S_a, S_b)}
$$

$$
ẑ_a = z_a + \frac{ d_n - d(S_a, S_b) }{2d(S_a, S_b)}
$$

$$
x̂_b = x_b + \frac{ d_n - d(S_a, S_b) }{2d(S_a, S_b)}
$$

$$
ŷ_b = y_b + \frac{ d_n - d(S_a, S_b) }{2d(S_a, S_b)}
$$

$$
ẑ_b = z_b + \frac{ d_n - d(S_a, S_b) }{2d(S_a, S_b)}
$$

当 d(Sₐ, S_b) ≥ dₙ

$$
x̂_a = x_a
$$

$$
ŷ_a = y_a
$$

$$
ẑ_a = z_a
$$

$$
x̂_b = x_b
$$

$$
ŷ_b = y_b
$$

$$
ẑ_b = z_b
$$

3.6 节点移动过程

步骤 1 启动整个网络环境，将总数为N的节点放置在长度为L、宽度为W、高度为H的待监测矩形区域，并转到步骤2。

步骤 2 每个节点需要进行时间校准，以确保各节点的时间一致。然后，在每个时间段tₙ内，所有节点向整个网络发送数据信息，主要内容包括其定位坐标和序列号。如果节点Sₐ接收到节点S_b发送的数据信息，则检查其存储的信息并进行更新，进入步骤3。

步骤 3 将节点S_b设置为节点Sₐ中存储的信息里序列号最小的节点，并进入步骤4。

步骤 4 节点a根据存储的信息计算节点Sₐ与节点S_b之间的距离，并转到步骤5。

步骤 5 计算节点Sₐ和节点S_b在tₙ时刻的距离以及欧几里得距离。如果d(Sₐ, S_b) < dₙ，计算节点Sₐ和节点S_b需要移动的新坐标(x̂ₐ, ŷₐ, ẑₐ)和(x̂_b, ŷ_b, ẑ_b)，然后转到步骤6。

步骤 6 如果节点Sₐ和节点S_b移动所需的新坐标(x̂ₐ, ŷₐ, ẑₐ)和(x̂_b, ŷ_b, ẑ_b)位于待监测区域之外，则终止节点Sₐ和节点S_b的移动，不再执行。如果节点Sₐ和节点S_b移动所需的新坐标位于待监测区域内，则执行节点Sₐ和节点S_b的移动，并同时转入步骤7。

步骤 7 如果邻居列表中存在尚未评估的节点，则转至步骤4并继续计算。如果邻居列表中的所有节点均已计算完毕，则转入步骤8。

步骤 8 如果计算过程中尚未用完周期，则转至步骤2并继续计算；如果计算过程中的所有周期均已用完，则算法结束并返回最终计算结果。

4 仿真

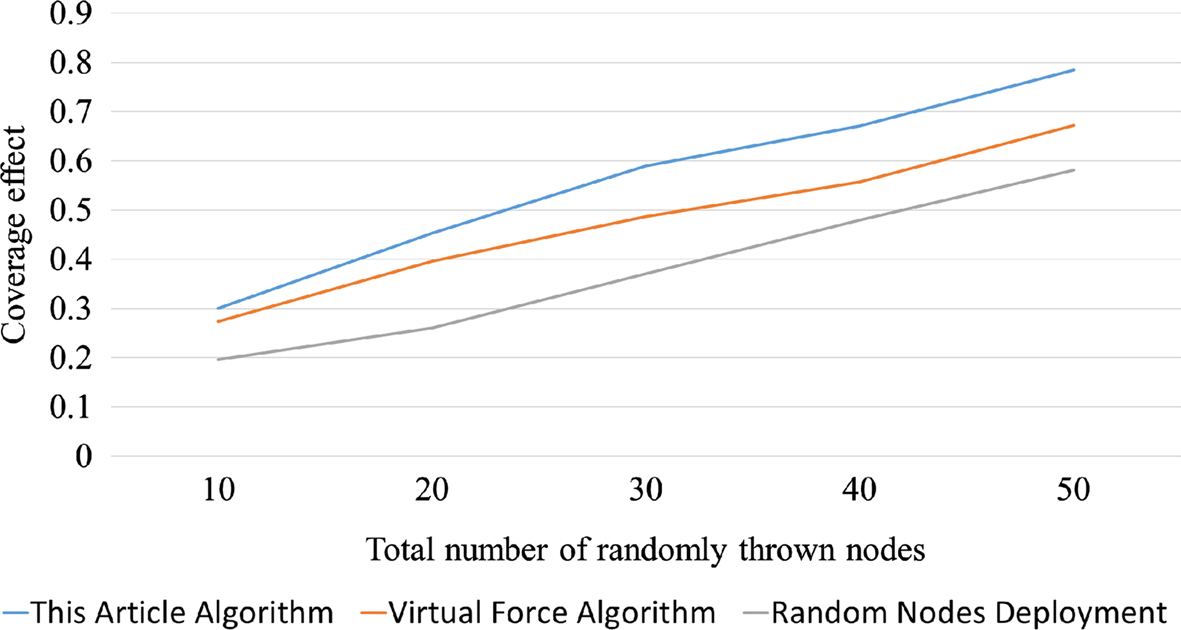
在监测区域中，长度L = 100 m，宽度W = 100 m，高度H = 100 m，节点的通信半径R_c = 60 m，节点的感知半径R_s = 20 m。随机投放的节点总数为N。

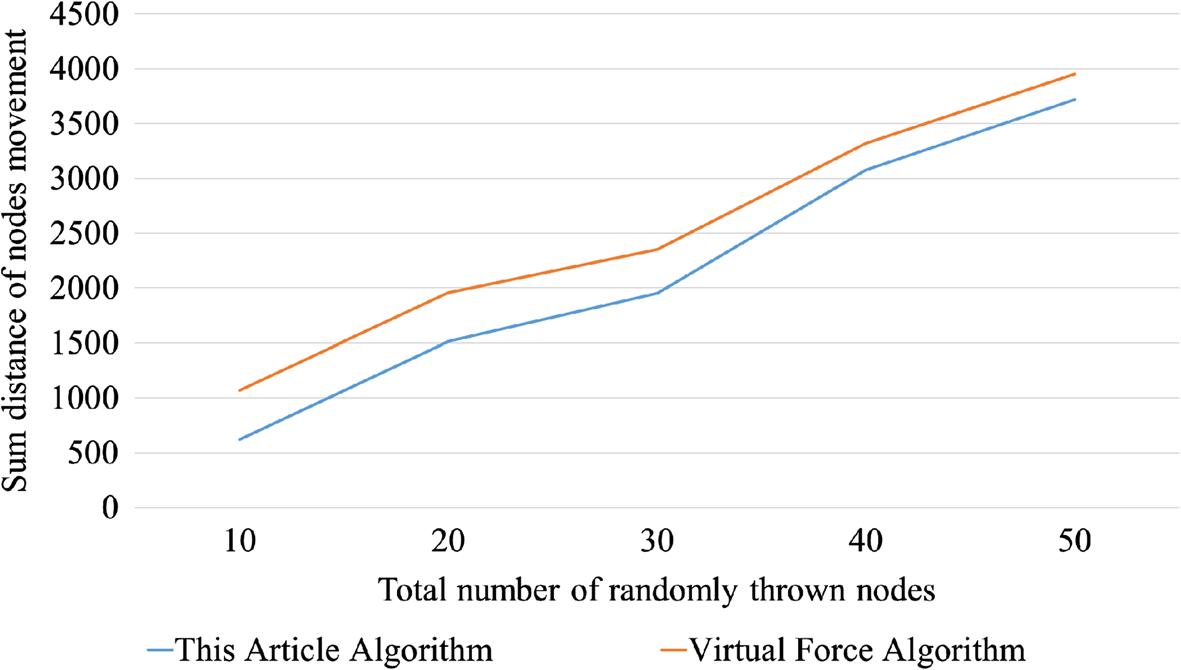
本文算法与虚拟力算法进行了比较[1]，结果如图1和2所示，其中N为= 10、20、30、40、50。

从图1和2中可以看出，该算法适用于大规模网络环境中的传感器节点部署。随着节点数量的增加，网络覆盖效果也随之提高。同时，可根据网络需求对传感器节点进行重新部署，具有很高的灵活性。在满足传感器节点之间连通性的前提下，实现了网络的最大覆盖。相比之下，与虚拟力算法相比，该算法具有更好的覆盖效果，并减少了节点的移动距离。

5 结论

无线传感器网络具有与其他信息获取方法不同的优点，例如无需固定设备支持、部署快速便捷、拓扑自组织、无有线网络约束。在无线传感器网络覆盖方面，提出了一种基于证据理论的动态网络覆盖算法。仿真结果表明，该算法能够实现对监测区域的完全覆盖，并有效减少节点的移动。如果由于某些原因需要重新部署网络，可以及时进行调整和重新部署，以满足监测区域的连通性。