巴特沃斯(Butterworth)滤波器（二）

wanrenqi

已于 2022-05-17 21:23:22 修改

阅读量1.6w

点赞数 16

分类专栏：滤波器设计方法文章标签：滤波器设计

于 2022-05-17 21:20:16 首次发布

原文链接：https://zhuanlan.zhihu.com/p/357619650

版权

滤波器设计方法专栏收录该内容

5 篇文章

订阅专栏

本文介绍了如何通过双线性变换将模拟滤波器转换为数字滤波器，详细阐述了转换过程和数学公式，并以二阶巴特沃斯滤波器为例，展示了从模拟到数字的转换步骤，包括直接I型和直接II型结构。同时，讨论了采样频率与截止频率的关系，以及如何优化滤波器结构减少延迟模块。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前面讲了下巴特沃斯（Butterworth）模拟滤波器的设计，这节讲下如何将模拟滤波器离散化，变成数字滤波器，然后在单片机中实现。

我们前面讲过很多离散化方法，其中最常用的一种叫做双线性变换
$\begin{aligned} s=\frac{2}{T_{s}}\frac{1-z^{-1}}{1+z^{-1}} \end{aligned}$
把这个公式代入传递函数就可以得到一个Z域的差分方程。
但是如果我们直接使用双线性变换进行离散化后，得到的数字滤波器和模拟滤波器的幅频响应曲线并不一样。
在这里插入图片描述
可以看出数字滤波器曲线，比模拟滤波器曲线衰减的要快，如果说模拟滤波器的截止频率为10rad/s,那么数字滤波器的截止频率只有9rad/s。

这是为什么呢，因为双线性变换是近似变换，不是准确换算。那么数字滤波器的截止频率fd和模拟滤波器的截止频率fa存在着什么样的对应关系呢？
在这里插入图片描述
所以在设计数字滤波器的时候，先确定数字滤波器的截止频率，再通过上式计算对应模拟滤波器的截止频率，最后通过双线性变换法离散化，得到Z域的差分方程。
但值得一提的是，当fs>>fd时，即采样频率远大于截止频率时，可以得到：
在这里插入图片描述
模拟滤波器的截止频率等于数字滤波器的截止频率。

数字滤波器的设置步骤

根据数字滤波器的截止频率计算得到对应的模拟滤波器的截止频率；
根据得到模拟滤波器的截止频率，将滤波器传递函数去归一化；
对模拟滤波器传函进行双线性变换；
写出代码

例如：
如果我们期望的数字滤波器的截止频率为fd，对应的模拟滤波器的截止角频率为：
$\begin{aligned} w_{a}=2\pi f_{a}=2f_{s}tan(\frac{\pi f_{d}}{f_{s}}) \end{aligned}$
去归一化只需要模拟滤波器传递函数中的s进行如下替换即可：
$\begin{aligned} s\rightarrow \frac{s}{w_{a}} \end{aligned}$
最后使用双线性变换离散化，把公式代入
$\begin{aligned} s=2f_{s}\frac{1-z^{-1}}{1+z^{-1}} \end{aligned}$
所以最终的变换方式就是
$\begin{aligned} s\rightarrow \frac{s}{w_{a}}=\frac{2f_{s}\frac{1-z^{-1}}{1+z^{-1}}}{sf_{s}tan(\frac{\pi f_{d}}{f_{s}})}=\frac{\frac{1-z^{-1}}{1+z^{-1}}}{tan(\frac{\pi f_{d}}{f_{s}})} \end{aligned}$
举个列子：
我们以归一化的二阶巴特沃斯滤波器公式为例
$\begin{aligned} H_{(s)}=\frac{1}{s^{2}+1.414s+1} \end{aligned}$

代入完整的变换可得：

我们令
$\begin{aligned} tan(\frac{\pi f_{d}}{f_{s}})=\Omega \end{aligned}$
![在这里插入图片描述](https://img-blog.csdnimg.cn/e0254113e85b4d408c944f6374a02afc.png
我们把上面差分方程写成代码：

const float fr = sample_freq/_cutoff_freq;
const float ohm = tanf(PI/fr);
const float c = 1.0f + 1.414f*ohm + ohm*ohm;

_b0 = ohm*ohm/c;
_b1 = 2.0f*_b0;
_b2 = _b0;

_a1 = 2.0f*(ohm*ohm - 1.0f)/c;
_a2 = (1.0f - 1.414f*ohm + ohm*ohm)/c;

for i = 1:10
	xn0 = sample(i);%采样数据
	yn0 = b0*xn0 + b1*xn1 + b2*xn2 - a1*yn1 - a2*yn2；
	yn2 = yn1；
	yn1 = yn0；
	xn2 = xn1;
    xn1 = xn0;
end

这种形式有个名称叫做直接I型，我们可以将它化成框图形式
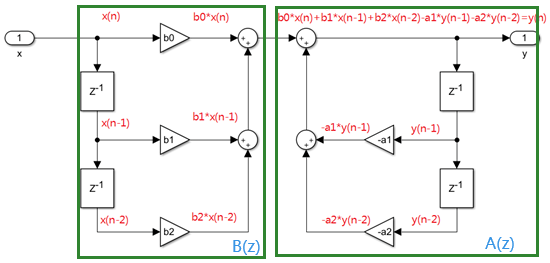
在这里插入图片描述

从框图中可以直观的看见使用了4个延时模块,从代码里也可以看见，我们需要保存4个过去的值；
一个二阶滤波器需要4个延时模块我们能不能化简一下呢？
我们可以把直接I型看成B(z)和A(z)两个模块串联而成的，从系统函数出发，调换其中B(z)和A(z)的顺序不影响系统输出。即：
在这里插入图片描述
仔细观察其实我们可以共用延时模块

这样我们只需要使用两个延时模块就行，这个叫做直接II型结构图，写成代码如下：

for i = 1:10
    d0 = sample(i) - d1*a1 -d2*a2;
    output = d0*b0 + d1*b1 + d2*b2;
    d2 = d1;
    d1 = d0;
end

这样一个巴特沃斯二阶低通数字滤波器就设置完成。

参考模型：https://download.youkuaiyun.com/download/wanrenqi/85367463
文章转载：https://zhuanlan.zhihu.com/p/357619650