数据挖掘04

数据挖掘04

1.反向传播算法

（1）定义

前向传播（Forward Propagation）：

是指输入数据从输入层到达输出层并产生预测结果的过程。

反向传播（Backpropagation）：

是根据输出结果和真实结果之间的差异，从输出单元开始，从后往前更新神经网络参数的过程。

联系：
前向传播和反向传播组成了神经网络模型训练的一个循环闭合过程。

（2）接下来，我们就来看看反向传播是怎么更新参数的？

举一个具体的例子，帮我们加深理解。

神经网络：一个三层网络（输入 → 隐藏 → 输出）

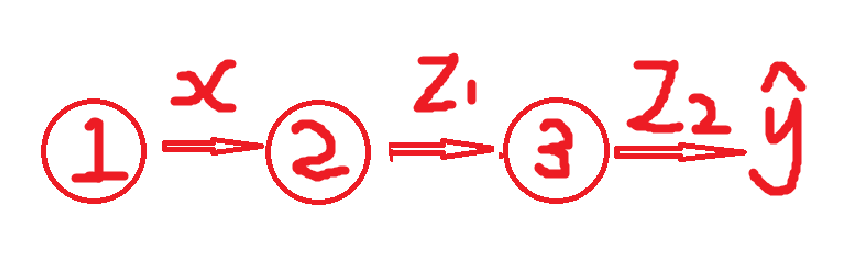
节点1：输入层，输入标量 x=2

节点2：隐藏层，z1 = w1x + b1, 激活后 a1 =σ(z1)
​
节点3：输出层，z2 = w2x + b2, 线性输出 ，预测值 y^ = z2

损失函数：

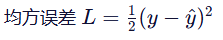
初始参数（随便设）：

w 1 =0.5, b 1 =0.1
w 2 =0.3, b 2 =0.2

开始前向传播了，计算过程如下：

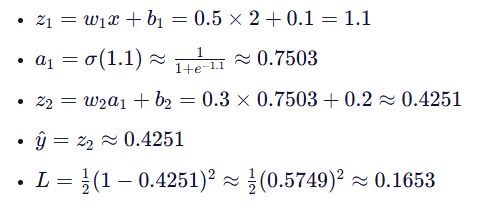
开始反向传播，计算梯度：

步骤 1：画出依赖路径

步骤2：计算出各项：

从后往前逐个计算（反向），这就是“反向传播”。

步骤三：最终得到梯度：

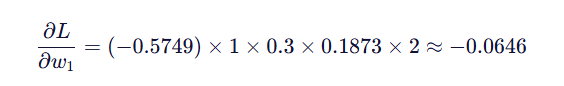
步骤4：更新参数，使用梯度下降：

更新 w 1：

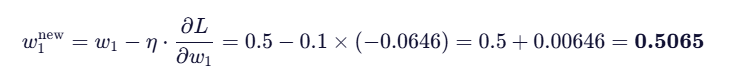
​看到这，您肯定明白了参数是怎么更新的了。

对每个参数都有：

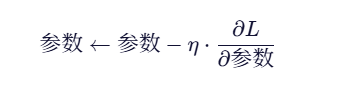
核心环节就是求梯度。

（3）梯度爆炸

出现原因：

链式法则求梯度，是多个导数的连乘。

如果这些导数的绝对值普遍大于 1，那么越往前（靠近输入层），梯度就会指数级放大。

（4）梯度消失

出现原因：

链式法则求梯度，是多个导数的连乘。

如果这些导数的绝对值普遍小于 1，那么越往前（靠近输入层），梯度就会指数级减小。

后边我们介绍解决方法。

2.最速梯度下降方法（Steepest Descent Method）

让我们会回顾下梯度是什么？

梯度的概念：

对于单变量函数，梯度就是导数；

对于多变量函数，梯度是一个向量，由所有偏导数组成。

梯度指向函数增长最快的方向。

（1）定义

定义梯度下降法（Gradient Descent） 的一种经典形式

核心思想是：
在每一步迭代中，沿着当前点处目标函数下降最快的方向（即负梯度方向）进行更新。

“最速下降”即指：每一步都沿这个最陡下降方向走。

有没有想问为什么要向下走？

是因为我们的训练目标是最小化损失函数（Loss Function），当然要向函数值减小的方向走。

（2）核心公式

（3）几何解释

请您想像，在参数空间中，损失函数 L(θ) 形成一个“地形”。

最速下降法就像一个人站在山坡上，每次都朝脚下最陡的下坡方向迈一步。

步长由学习率 η 控制：
太小 → 走得慢，收敛慢
太大 → 可能跨过谷底，震荡甚至发散

3.随机梯度下降法（Stochastic Gradient Descent, SGD）

（1）定义

它是梯度下降法（Gradient Descent） 的一种高效近似版本。

核心思想是：

每次更新参数时，只用一个（或一小批）样本来估计梯度，而不是使用全部训练数据。

（2）为什么只用一个（或一小批）样本来估计梯度，而不是使用全部训练数据。这样设计是为了解决什么问题？

回答：
是为了解决 计算效率问题，原来全部参数更新一次，必须遍历整个训练集（来计算精确梯度，每一步都要做 O(N) 次前向+反向传播（N 是样本总数），在大数据时代（ImageNet 有 1400 万图像，语言模型训练数据达 TB 级），等一次更新可能要几小时甚至几天。

（3）SGD工作流程

“随机打乱 + 分批采样”

举个例子：
假设有：
训练集有 N=10,000 个样本
batch size B=64

**步骤 1：**每个 epoch 开始前，打乱（shuffle）数据顺序

一个 epoch 指的是整个训练数据集被完整遍历一次的过程。

**步骤 2：**将打乱后的数据按 batch size 切分成若干批（batches）

总批数 ≈ ⌈N/B⌉=⌈10000/64⌉=157 批

前 156 批：每批 64 个样本

最后一批：10000−156×64=16 个样本（可丢弃或保留）

**步骤 3：**按顺序遍历每个 batch，用于一次参数更新

下一个 epoch 再次打乱，重新分批。

（4）两种方法比较分析

梯度下降：

先问遍所有人（100个），汇总成一份完整报告，然后改一次教案。

SGD：

先随机找 5 个人聊，立刻微调教案；

再找另外 5 个人（用新教案问），再微调；

重复 20 次，直到问完100人。

总共改了 20 次教案，而且后面的人是在你已经修改过的教案基础上给反馈的！

所以，虽然“用完了全部数据”，但不是“一次性用全部数据更新”，而是“分多次、边看边改”。

如果您有高见或者不解，可以留言，看到必回。