数据挖掘05

数据挖掘05

书接上回

1.包含动量的随机梯度下降算法

（1）定义

包含动量的随机梯度下降（Momentum Stochastic Gradient Descent, 简称 SGD with Momentum）是一种在标准随机梯度下降（SGD）基础上引入“动量”项的优化算法，旨在加速收敛、减少震荡，并帮助模型跳出局部极小值或鞍点。

（2）复习一下上一篇介绍过的SGD

标准 SGD 在每次迭代中使用一个样本（或一个小批量）来估计梯度并更新参数，公示如下：

缺点：

1）更新方向完全依赖当前梯度，容易产生高方差和震荡；

2）在狭窄峡谷或非凸地形中收敛缓慢；

3）容易陷入局部最优或鞍点。

(3)更新方向完全依赖当前梯度，为什么容易产生高方差和震荡?

因为每次根据样本估计的梯度可能与真实梯度方向相差很远，
所以会出现：

有时更新方向接近最优；

有时却几乎垂直甚至反向；

导致参数在最优解附近来回震荡，而不是平稳靠近。

举个例子：

假设你在一个嘈杂的房间里听人说话。每次只听一个词（SGD），这个词可能是“向左”也可能是“向右”，即使整体趋势是“向前”。你每一步都按听到的词走，就会左右乱晃。

（4）为什么SGD在狭窄峡谷或非凸地形中收敛缓慢？

狭窄峡谷：
例子：
在一条深而窄的山谷里想走到谷底最低点。每次你只看脚下最陡的方向往下跳，结果就是不断撞到左右岩壁，前进效率极低。

非凸地形：

存在大量鞍点（saddle points） 和平坦区域（plateaus）；

SGD 在平坦区域梯度接近零 导致更新几乎停滞；

复习完毕，我们看下带动量的SGD

（5） 动量机制的引入

动量方法借鉴了物理学中的“惯性”概念：参数更新不仅考虑当前梯度，还累积过去梯度的方向，形成一种“速度”。

动量 SGD 的更新公式：

动量是历史梯度的加权和，形成一个惯性速度。

动量不是只记住“上一次”的梯度，而是综合了最近若干次梯度的方向和大小。

（6）动量的作用：

1）平滑更新方向：通过指数加权平均历史梯度，减少随机噪声的影响。

2）加速收敛：在一致方向上持续加速（如沿峡谷底部）。

3）帮助逃离平坦区域：即使当前梯度很小，若之前有动量，仍可继续移动。

2.Adagrad算法

（1）定义

AdaGrad（Adaptive Gradient Algorithm） 是一种自适应学习率优化算法。

核心思想是：
为每个参数分配一个独立的学习率，根据该参数的历史梯度大小自动调整。
梯度大的参数学习率变小，梯度小的参数学习率变大。

（2）为什么需要自适应学习率？

我们知道，在标准 SGD 中：

所有参数都使用同一个全局学习率 η；

但不同参数的重要性、更新频率、梯度尺度可能差异巨大。

所以，为了解决这个问题，引入自适应学习率，让每个参数“按需调整步长”。

（3）公式

调节学习率的原理：

（4）性质

优点：

特别适合稀疏数据（如自然语言处理、推荐系统中的嵌入层），能显著提升收敛速度和性能。

缺点：

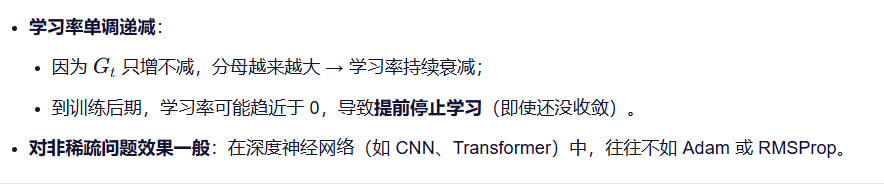
3.RMSprop算法

（1）定义

RMSProp（Root Mean Square Propagation） 是一种自适应学习率优化算法。

核心思想是：

对 AdaGrad 进行改进，通过引入指数移动平均（EMA）来“遗忘”久远的梯度信息，从而避免学习率过早衰减到零的问题。

（2）回顾 AdaGrad：

它累积所有历史梯度的平方和：

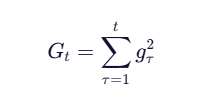
这会导致学习率分母持续增大 → 学习率单调下降 → 训练后期几乎停止更新。

为了解决这个问题，我们提出了RMSprop。

（3）公式：

对每个参数（或整体向量形式），RMSProp 的更新规则如下：

（4）性质

1）指数移动平均（EMA）

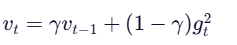
这样就能更好的调节学习率：

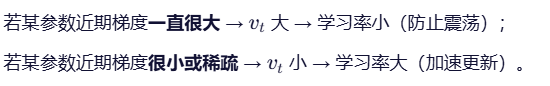
2）避免学习率崩溃

因为旧梯度被遗忘 ， 所以 vt 不会无限增长，分母不会趋于无穷；

学习率可以在训练后期保持一定活性，适合长时间训练。

4.Adam算法

Adam（Adaptive Moment Estimation）算法是自适应学习率优化算法。

结合了动量法和RMSProp的优点，能够高效地处理非平稳目标函数，并在实践中表现出良好的收敛性能。

（1） 核心思想

Adam 同时维护两个移动平均：

一阶矩估计（First moment）：梯度的指数加权平均（类似动量）。
二阶矩估计（Second moment）：梯度平方的指数加权平均（类似 RMSProp）。

然后对这两个矩进行偏差修正（bias correction），以解决初始阶段估计偏小的问题

（2）算法步骤

（3） 优点

自适应学习率：不同参数可有不同的更新步长。

对梯度噪声鲁棒。

通常收敛速度快，适合大规模数据和高维参数空间。

实现简单，只需设置少量超参数。

（4）缺点

在某些凸问题上可能不如 SGD + 动量稳定。

可能会“过早收敛”或陷入次优解（尤其在泛化敏感的任务中）。

超参数（尤其是学习率）仍需调优。

5.AdamW算法

AdamW（Adam with Weight Decay）是 Adam 优化器的一个改进版本。

在Adam的基础上，修正了Adam算法对于所有参数的权重衰减相同的问题，加入了权重衰减系数。

参数更新公式：

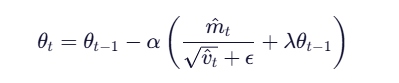
至此，我们介绍完了优化器算法。

什么是优化器呢？

“优化器”指的是用于更新模型参数以最小化损失函数的算法。