数据挖掘03
一、多层感知机与神经网络
1.人类大脑与神经元
大脑里边大约有1000亿个神经元,神经元组成了神经网络。
神经元之间通过突触传递电信号。
一个神经元有1000个突触。
2.人工神经网络模型
顾名思义,模拟大脑的神经网络建立的模型,就是神经网络模型。
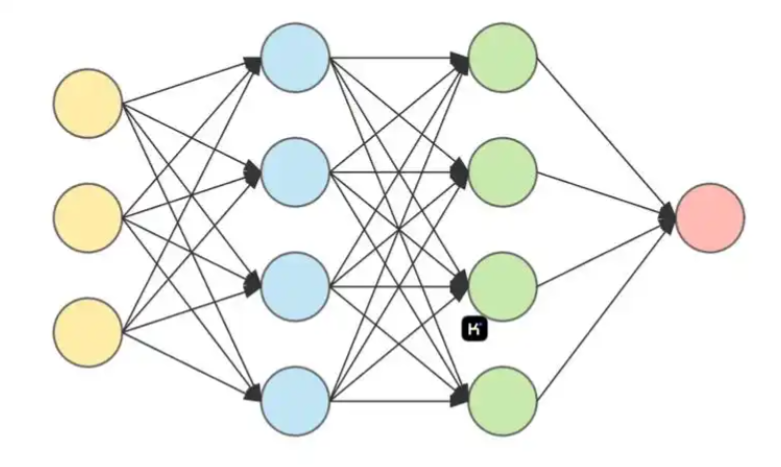
那么,
怎么模拟的呢?
节点对应神经元
节点之间的连接对应突触
同时,
每个节点设置激活函数,激活函数决定这些信号是否以及如何被“激发”并继续传播。
连接的强度用一个权重表示。
3.感知器与多层感知器

从结果我们可以看出来,感知器能使实现二分类。
4.线性回归和逻辑回归
线性回归(Linear Regression)和逻辑回归(Logistic Regression)是机器学习中最基础、最常用的两种监督学习模型,分别用于解决回归问题和分类问题。
虽然名字里都有“回归”,但它们的目标、输出形式和数学原理有显著区别。
(1)线性回归(Linear Regression)
用途:预测连续数值

目的:试图画一条“最佳拟合直线”穿过数据点。
(2)逻辑回归(Logistic Regression)

目的:
试图画一条“分界线”,使得两类样本尽可能分开,并给出每个点属于某类的置信度。
所以,逻辑回归是线性分类器。
您是不是发现了:
逻辑回归就是在线性回归的基础上多了一步非线性变换(Sigmoid 函数)
例题:
线性回归难以建模处理二分类问题,而 logistic 回归能处理二分类问题,关于其原因,说法错误的是:
A. 线性回归无论对输入进行怎样的加权操作,都只能得到一个线性模型,不能表示复杂、非线性的模式和关系
B. Logistic 函数能够完美地建模二分类中的非线性关系
C. Logistic 函数将加权输入进行“扭曲”,是一种非线性操作,因此能够建模非线性关系
答案:B
原因:虽然 Logistic 函数本身是非线性的,但是它不能建模复杂的非线性关系,只能处理线性可分的数据,是线性分类器。
5.全连接神经网络
定义:
顾名思义,前一层的每一个神经元节点均与后一层的每一个神经元节点相连接。
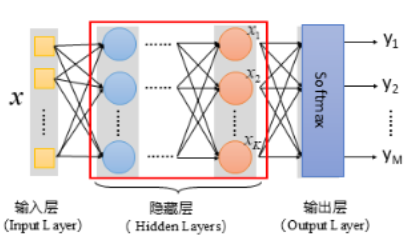
6.激活函数
(1)Sigmoid函数
作用:将任意实数映射到 (0, 1) 区间。
最常用的 Sigmoid 函数形式为:
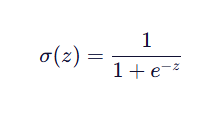
图像如下:
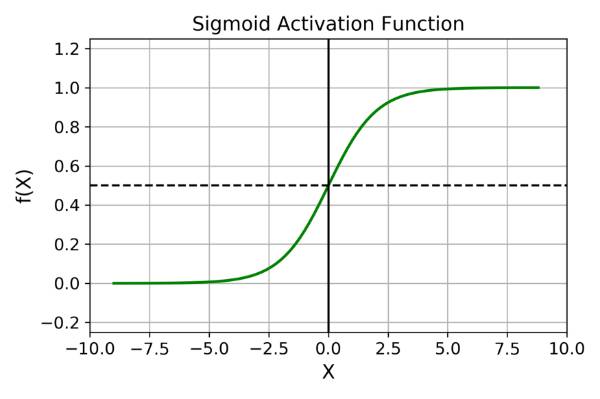
常用于二分类任务。
思考:如何改进sigmoid函数,使得改进后的函数能输出正值、负值?
方法:
1.σ(z)−0.5 ,图像向下平移,输出为(-0.5 , 0.5)
2.2σ(z)−1 , 将 Sigmoid 的输出从 (0, 1) 映射到 (-1, 1)
方法2更优。
(2)Tanh函数
Tanh函数(双曲正切函数,Hyperbolic Tangent Function)
1.数学表达式:
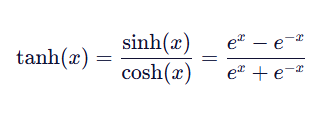
2.图像:
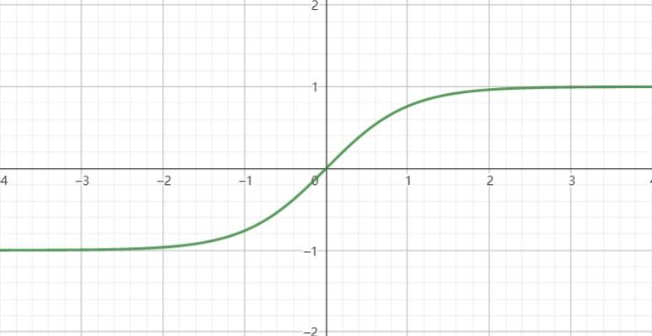
3.性质:
奇函数:tanh(−x)=−tanh(x)
值域:(−1,1)
平滑可导:处处连续且可微
4.Tanh 函数的导数形式简洁,便于反向传播计算:(后面会讲反向传播)
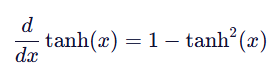
看完上面两个激活函数,您肯定发现了Sigmoid函数和Tanh函数的图形一样。
没错!他们二者存在明确的缩放和平移关系:
用数学公式表达:
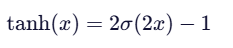
我们可以说:
Tanh 函数本质上是经过缩放和平移的 Sigmoid 函数。
(3)Softmax激活函数
1.核心作用:
将一个任意实数向量转换为一个概率分布
即输出的每个元素都在 (0,1) 之间
且所有元素之和为 1。
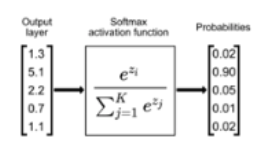
2.数学公式:
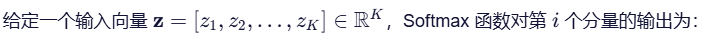
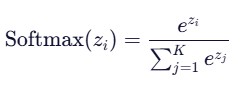
其中,
分母是所有指数项之和。
分子就是各个指数项。
显而易见,输出总和为 1。
3.正是Softmax 的“输出总和为 1”这一特性,使得Softmax用于输出层。
解释:
在多分类任务中(比如识别一张图是猫、狗还是鸟),我们希望模型回答:
“这张图属于每个类别的可能性有多大?”
那这就要求:
要求一:每个类别的预测值应在 (0,1) 之间
要求二:所有类别可能性加起来应为 1(因为“必属于某一类”)
Softmax 完美满足要求,所以他常用于输出层。
4.当类别数 K=2(即二分类)时,Softmax 函数在数学上等价于 Sigmoid 函数。
解释:

(4)ReLU激活函数
ReLU(Rectified Linear Unit,修正线性单元)
1.数学定义:
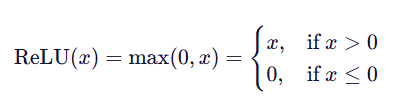
2.图像:
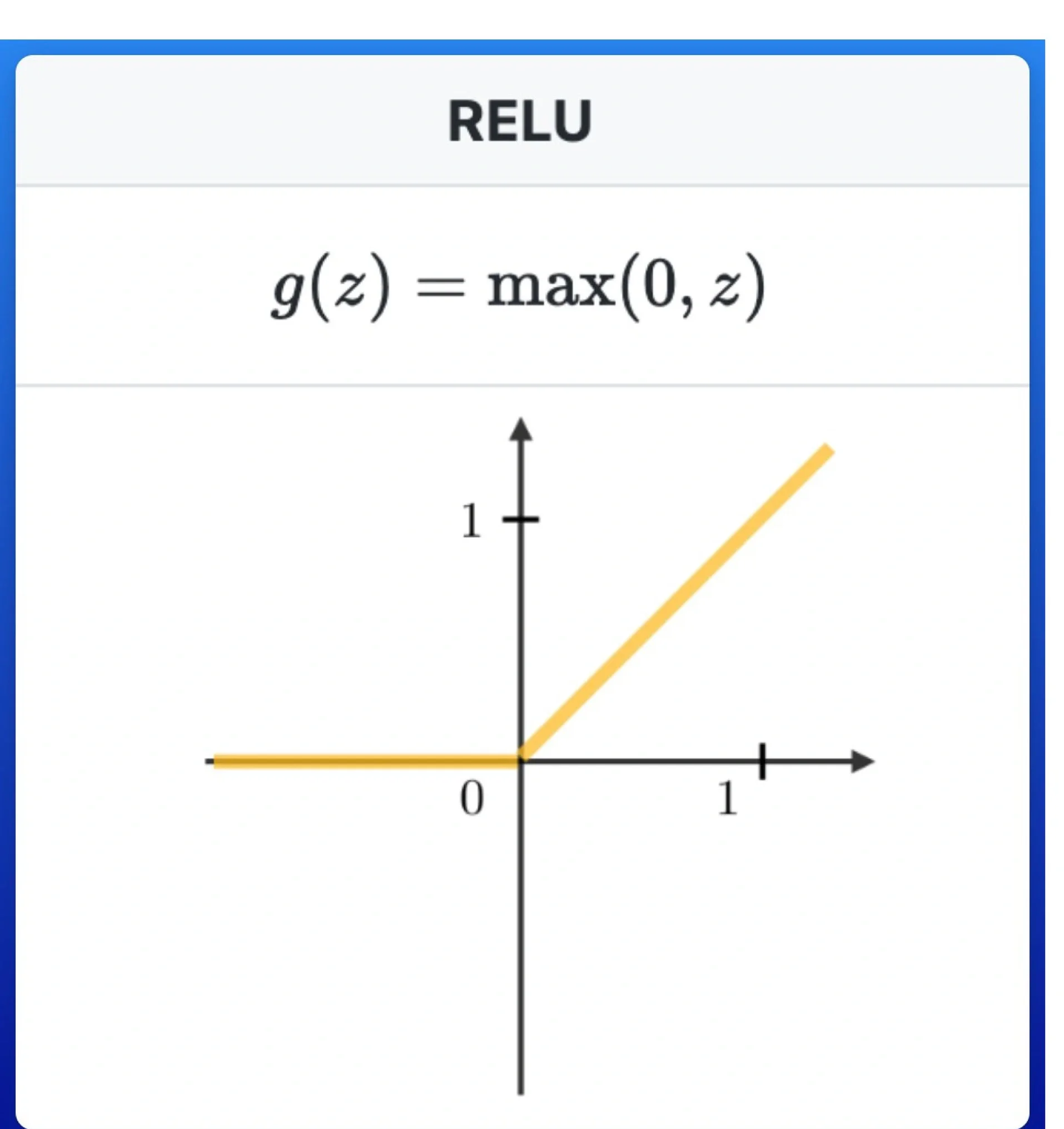
3.性质:
1)非线性:虽然分段线性,但整体是非线性的
2)导数简单:

3)缓解梯度消失:正区导数恒为 1,反向传播时梯度不会衰减(相比 Sigmoid/Tanh)
补充梯度的概念:
对于单变量函数,梯度就是导数;
对于多变量函数,梯度是一个向量,由所有偏导数组成。
梯度指向函数增长最快的方向。
4)可能出现“神经元死亡”(Dying ReLU Problem)现象:
指的是:
某些神经元在训练过程中永远输出 0,且不再对任何输入产生响应,梯度也无法更新其参数。
原因解释:
导数公式:
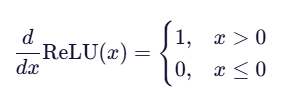
由导数定义,我们可以知道:
a.当输入 x≤0 时,梯度为 0;
数学定义:
ReLU(x)=max(0,x)
由公式定义,我们可以知道:
b.当输入 x≤0 时,输出为 0;
那么,我们开始假设:
如果某次前向传播时,某个神经元的输入 z < 0;
就会有
该神经元输出为 0(由b得到)
且反向传播时梯度也为 0(由a得到)
这会导致权重 和偏置 无法更新。
该神经元就可能永远卡在负值区域,再也“活”不过来 , 这就是神经元死亡。
(5) Softplus激活函数
Softplus 激活函数 是 ReLU(Rectified Linear Unit)的一种平滑近似。
在保持 ReLU 多数优点的同时,
解决了其不可导(在 0 点)和“神经元死亡”等问题。
数学公式:
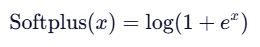
图像:
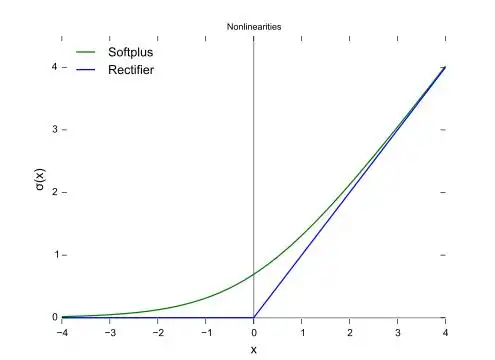
Softplus 可以看作是 ReLU 的“软化版”:

当 x 较大时,两者几乎重合
当 x 接近或小于 0 时,Softplus 平滑地趋近于 0,而 ReLU 直接截断为 0
(6)GeLU激活函数
GELU(Gaussian Error Linear Unit)
1.数学定义
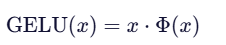
具体来说,GELU 将输入 x 视为来自标准正态分布的样本,并计算:
“有多少比例的值小于等于 x”,然后用这个概率加权 x 本身。
其中,

2.图像
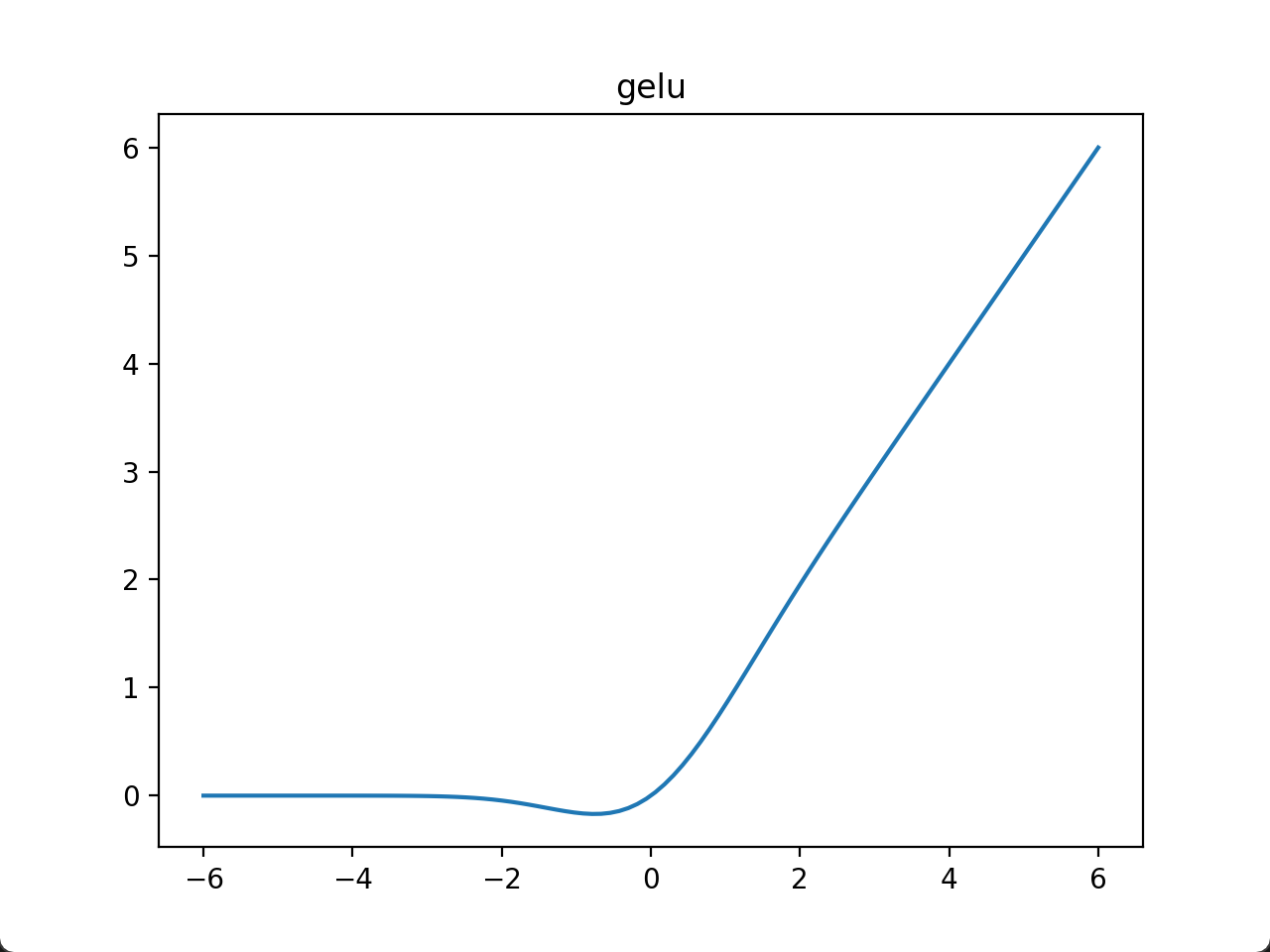
7.损失函数
损失函数(Loss Function)
衡量模型预测值与真实目标之间的差距
是模型训练过程中优化的目标
损失函数的值越小,模型拟合训练集的程度就越高。
8.平均绝对误差函数
平均绝对误差函数(Mean Absolute Error, MAE)
衡量的是模型预测值与真实值之间绝对误差的平均大小。
1.数学公式:
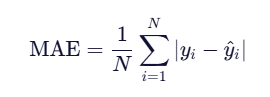
其中,

2.性质
1)0处不可导
解释:
MAE 的基本单元是绝对误差。

图像是V字形,顶点在原点 (0, 0)
左侧斜率为 -1,右侧斜率为 +1
由高等数学的知识,我们知道,
在0处,左导数 不等于 右导数
所以,在0处不可导
2)常用于有监督学习的回归任务
解释:
首先明确:什么是有监督学习的回归任务?

所以,使用MAE衡量误差,逻辑自然。
其次,对比分类任务:标签是离散类别(如“猫”“狗”),不能直接相减,不能用 MAE。
9.均方误差函数
均方误差(Mean Squared Error, MSE)
对预测误差进行平方后取平均,
“均”:对所有样本取平均(mean)
“方”:对误差取平方(squared)
所以叫均方。
1.数学公式:
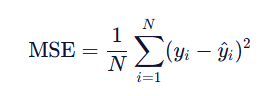
2.性质
1)处处可导
导数公式:
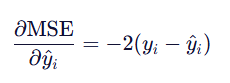
2)误差越大,梯度越大
由导数公式,我们可以看出:
梯度大小与误差成正比
10.交叉熵函数
交叉熵(Cross-Entropy)
1)分类
有两类:
多分类交叉熵(Categorical Cross-Entropy)
二分类交叉熵(Binary Cross-Entropy, BCE)
11.KL-散度
KL 散度(Kullback-Leibler Divergence),又称相对熵(Relative Entropy)
衡量两个概率分布之间差异
12.防止过拟合的措施
什么是过拟合?
模型在训练集上表现很好,但在测试集上性能差。
根本原因:模型参数过多、过于灵活,拟合了噪声和无关细节。
(1)损失函数的正则化
正则化的核心思想:
“在拟合能力和模型简洁性之间做权衡” —— 奥卡姆剃刀原则
定义:
总损失函数 = 原始损失 + 正则化项
公式如下:

其中,
λ≥0:正则化强度超参数
λ=0:无正则化
λ 越大,模型越“简单”,但可能欠拟合
常见的两个正则化方法:
L1 正则化(Lasso)
L2 正则化(Ridge Regression / Weight Decay)
(2)随机丢弃
在每次训练迭代中,以一定概率 p(如 0.5)临时将某些神经元的输出置为 0。
这样,模型被迫不依赖任何单个神经元。
例题

答案:A





















 4257
4257

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








