VL12 4bit超前进位加法器电路

VL12 4bit超前进位加法器电路

预备知识

1. 行波进位加法器
   
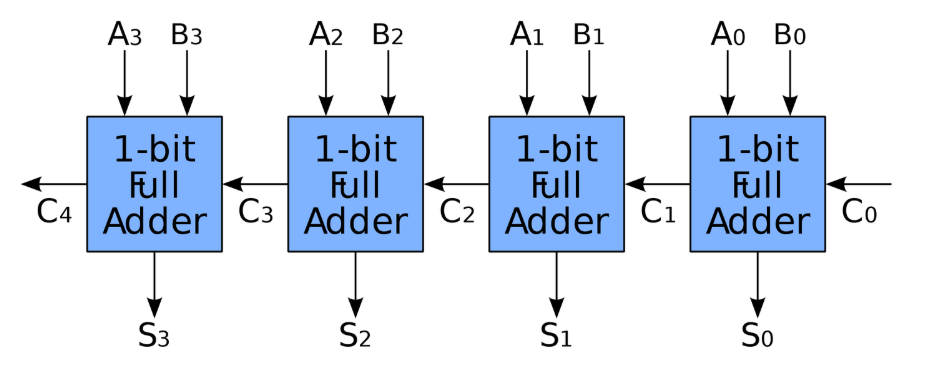
   可以看出，这是个串行结构。
   高位的计算结果需要低级进位，也就是，低位没有计算出进位，高位就无法计算，得等待。
2. 并行进位加法器

计算逻辑：

核心思想：
把 C1~C4 全部用原始输入（A, B, Cin）直接表示出来，不依赖中间进位！

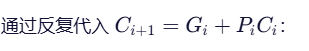
得到：

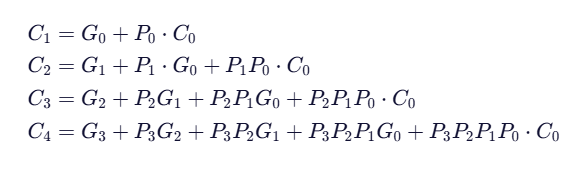
但是硬件代价增大，需要更多的逻辑门，比如C4的计算电路如下：

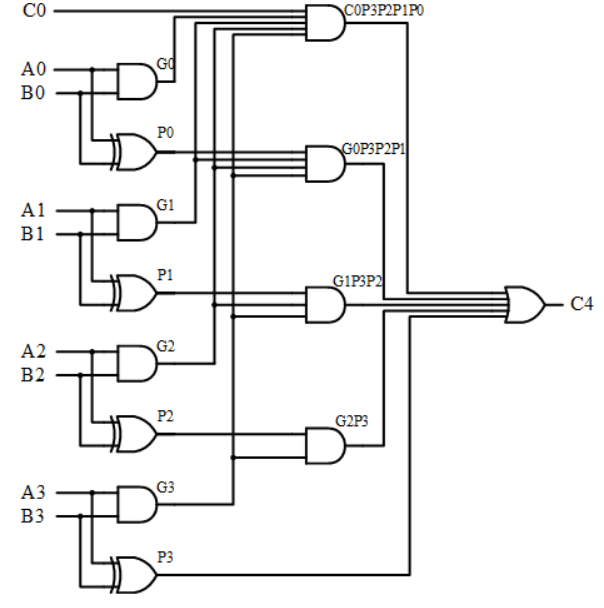
题目要求

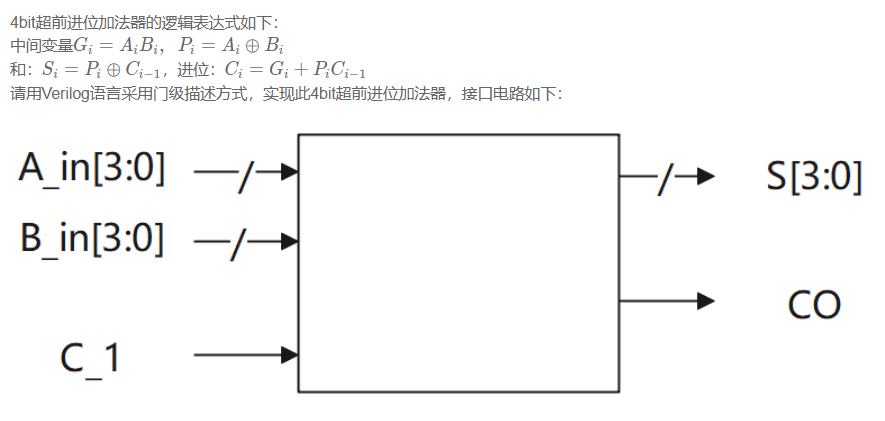
思路一：

`timescale 1ns/1ns

module lca_4(
	input		[3:0]       A_in  ,
	input	    [3:0]		B_in  ,
    input                   C_1   ,
 
 	output	 wire			CO    ,
	output   wire [3:0]	    S
);
    wire [2:0] c;
	assign c0 = A_in[0]&B_in[0] | A_in[0]^B_in[0] & C_1 ;
	assign c1 = A_in[1]&B_in[1] | A_in[1]^B_in[1] & (A_in[0]&B_in[0] | A_in[0]^B_in[0] & C_1 );
	assign c2 = A_in[2]&B_in[2] | A_in[2]^B_in[2] & (A_in[1]&B_in[1] | A_in[1]^B_in[1] & (A_in[0]&B_in[0] | A_in[0]^B_in[0] & C_1 ));
	assign CO = A_in[3]&B_in[3] | A_in[3]^B_in[3] & (A_in[2]&B_in[2] | A_in[2]^B_in[2] & (A_in[1]&B_in[1] | A_in[1]^B_in[1] & (A_in[0]&B_in[0] | A_in[0]^B_in[0] & C_1 )));
	assign S[0] = A_in[0]^B_in[0]^C_1;
	assign S[1] = A_in[1]^B_in[1]^(A_in[0]&B_in[0] | A_in[0]^B_in[0] & C_1);
	assign S[2] = A_in[2]^B_in[2]^ (A_in[1]&B_in[1] | A_in[1]^B_in[1] & (A_in[0]&B_in[0] | A_in[0]^B_in[0] & C_1 ));
	assign S[3] = A_in[3]^B_in[3]^(A_in[2]&B_in[2] | A_in[2]^B_in[2] & (A_in[1]&B_in[1] | A_in[1]^B_in[1] & (A_in[0]&B_in[0] | A_in[0]^B_in[0] & C_1 ))) ;

endmodule

思路二：

`timescale 1ns/1ns

module lca_4(
    input  [3:0] A_in,
    input  [3:0] B_in,
    input        C_1,
    output       CO,
    output [3:0] S
);

    wire [3:0] G = A_in & B_in;
    wire [3:0] P = A_in ^ B_in;

    wire c0 = C_1;
    wire c1 = G[0] | (P[0] & c0);
    wire c2 = G[1] | (P[1] & G[0]) | (P[1] & P[0] & c0);
    wire c3 = G[2] | (P[2] & G[1]) | (P[2] & P[1] & G[0]) | (P[2] & P[1] & P[0] & c0);
    wire c4 = G[3] | (P[3] & G[2]) | (P[3] & P[2] & G[1]) | (P[3] & P[2] & P[1] & G[0]) | (P[3] & P[2] & P[1] & P[0] & c0);

    assign S = P ^ {c3, c2, c1, c0};
    assign CO = c4;

endmodule

请思考问题：思路一、思路二哪个是并行计算？
答案：思路二

比较分析：
思路一是按照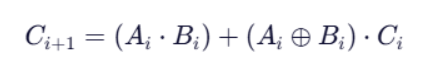
展开写的。但是这并不是并行计算，虽然看似像，但不是。
因为
每一步都依赖上一步的输出，高位必须等待低位计算完成。
看代码：

assign c0 = A_in[0]&B_in[0] | A_in[0]^B_in[0] & C_1 ;
assign c1 = A_in[1]&B_in[1] | A_in[1]^B_in[1] & (A_in[0]&B_in[0] | A_in[0]^B_in[0] & C_1 );

这种展开的嵌套写法就像g(m(f(x))),
要先计算最内层的f(x)
同样，
计算c1，要先计算括号部分：(A_in[0]&B_in[0] | A_in[0]^B_in[0] & C_1 )
括号部分就是c0。
所以，这不是并行逻辑。
我们说过：
并行的核心：把 C1~C4 全部用原始输入（A, B, Cin）直接表示出来，不依赖中间进位！
思路二是真正的并行计算，只用到P、G、c0