http://en.wikipedia.org/wiki/Histogram_equalization
Examples
Small image
The following is the same 8x8 subimage as used in JPEG. The 8-bit greyscale image shown has the following values:
The histogram for this image is shown in the following table. Pixel values that have a zero count are excluded for the sake of brevity.
-
Value Count Value Count Value Count Value Count Value Count 52 1 64 2 72 1 85 2 113 1 55 3 65 3 73 2 87 1 122 1 58 2 66 2 75 1 88 1 126 1 59 3 67 1 76 1 90 1 144 1 60 1 68 5 77 1 94 1 154 1 61 4 69 3 78 1 104 2 62 1 70 4 79 2 106 1 63 2 71 2 83 1 109 1
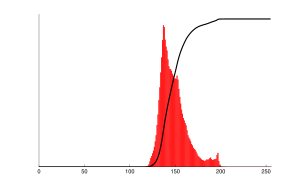
The cumulative distribution function (cdf) is shown below. Again, pixel values that do not contribute to an increase in the cdf are excluded for brevity.
-
Value cdf cdf, scaled 52 1 0 55 4 12 58 6 20 59 9 32 60 10 36 61 14 53 62 15 57 63 17 65 64 19 73 65 22 85 66 24 93 67 25 97 68 30 117 69 33 130 70 37 146 71 39 154 72 40 158 73 42 166 75 43 170 76 44 174 77 45 178 78 46 182 79 48 190 83 49 194 85 51 202 87 52 206 88 53 210 90 54 215 94 55 219 104 57 227 106 58 231 109 59 235 113 60 239 122 61 243 126 62 247 144 63 251 154 64 255
This cdf shows that the minimum value in the subimage is 52 and the maximum value is 154. The cdf of 64 for value 154 coincides with the number of pixels in the image. The cdf must be normalized to![[0,255]](http://upload.wikimedia.org/math/8/9/d/89dd46dfd5ac422d57ddaa6237c56f8c.png) . The general histogram equalization formula is:
. The general histogram equalization formula is:
Where cdfmin is the minimum non-zero value of the cumulative distribution function (in this case 1), M × N gives the image's number of pixels (for the example above 64, where M is width and N the height) and L is the number of grey levels used (in most cases, like this one, 256). The equalization formula for this particular example is:
For example, the cdf of 78 is 46. (The value of 78 is used in the bottom row of the 7th column.) The normalized value becomes
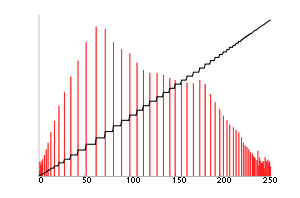
Once this is done then the values of the equalized image are directly taken from the normalized cdf to yield the equalized values:
Notice that the minimum value (52) is now 0 and the maximum value (154) is now 255.







 本文详细介绍了直方图均衡化的概念、原理及其在图像处理中的应用。通过具体例子展示了如何利用直方图均衡化提高图像对比度和视觉效果。文章深入分析了直方图均衡化过程中的关键步骤,包括直方图计算、累积分布函数(CDF)生成及均衡化公式应用,最终呈现了原图与均衡化后图像的对比,清晰地展示了直方图均衡化的效果。
本文详细介绍了直方图均衡化的概念、原理及其在图像处理中的应用。通过具体例子展示了如何利用直方图均衡化提高图像对比度和视觉效果。文章深入分析了直方图均衡化过程中的关键步骤,包括直方图计算、累积分布函数(CDF)生成及均衡化公式应用,最终呈现了原图与均衡化后图像的对比,清晰地展示了直方图均衡化的效果。



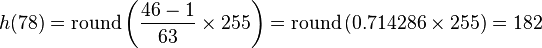


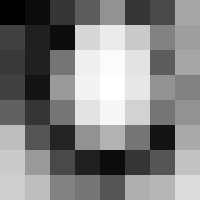


















 743
743

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








