C++ 二分法查找

思路

前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

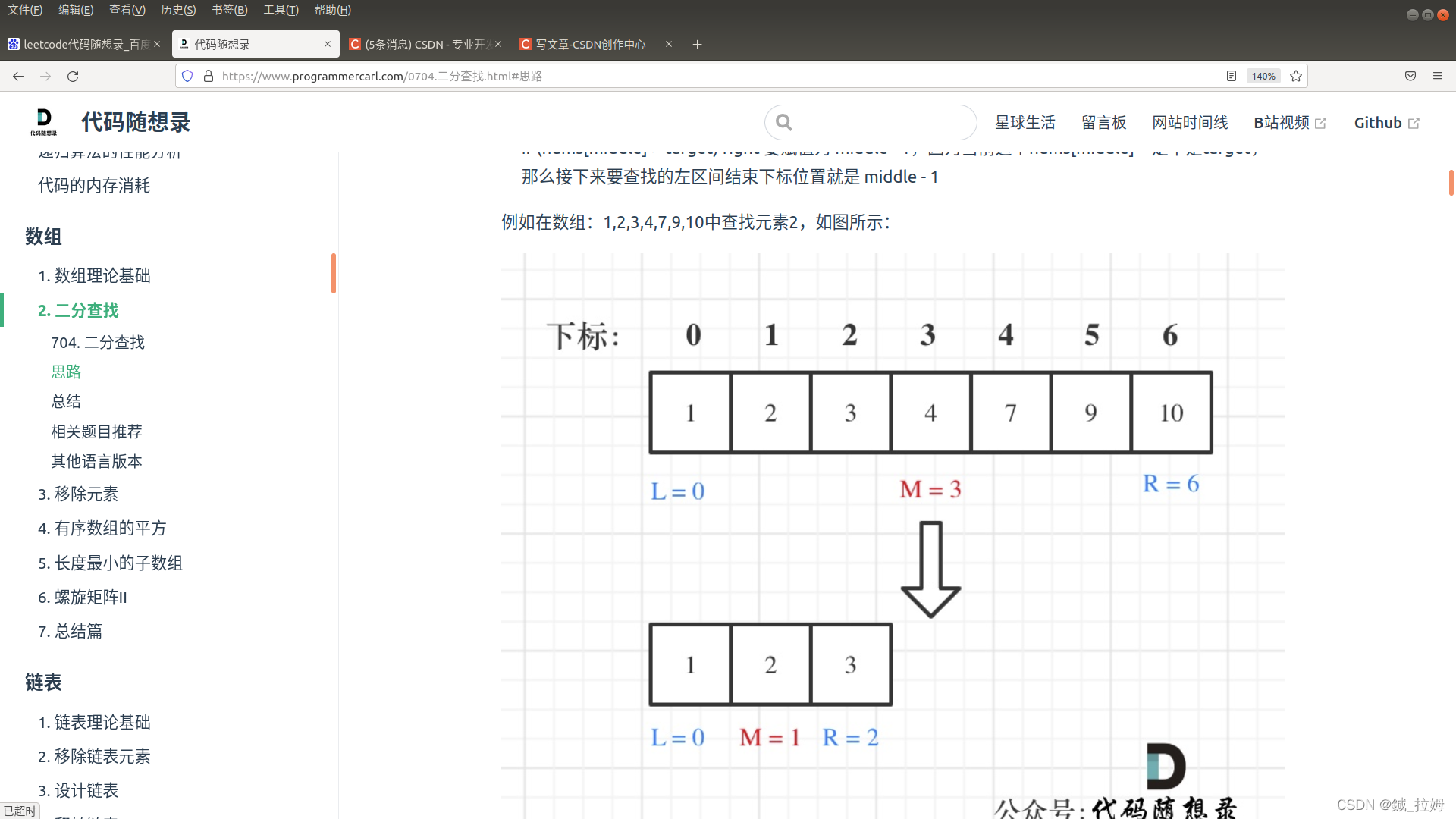
方法一：寻找区间[left,right],right=arr.size()-1:

 代码

#include<iostream>
#include<string.h>
#include <vector>
using namespace std;

void erfen_find(vector<int> &arr,int a)//二分法查找函数
{

    int left=0;
    int right=arr.size()-1;
    while (left<=right)
    {
        int mid=(left+right)/2;
        if (arr[mid]>a)
        {
            right=mid-1;
        }
        else if (arr[mid]<a)
        {
            left=mid+1;
        }
        else
        {
            cout<<"索引：  "<< mid<<endl;
            break;
        }
    }
}

int main()
{
    vector<int>arr;//创建【1，2，3，4，5】
    for (int i=0;i<5;i++)
    {
        arr.push_back(i+1);
    }
    int a;
    cout<<"输入需要查找的值"<<endl;
    cin>>a;
    erfen_find(arr,a);
    return 0;
}

结果：

输入需要查找的值
3
索引：  2

方法二：寻找区间[left,right）,right=arr.size():其思路其实还是和方法一样的，只是话换了个区间而已。

#include<iostream>
#include<string.h>
#include <vector>
using namespace std;

void erfen_find(vector<int> &arr,int a)
{

    int left=0;
    int right=arr.size();
    while (left<right)
    {
        int mid=(left+right)/2;
        if (arr[mid]>a)
        {
            right=mid;
        }
        else if (arr[mid]<a)
        {
            left=mid+1;
        }
        else
        {
            cout<<"索引：  "<< mid<<endl;
            break;
        }
    }
}

int main()
{
    vector<int>arr;
    for (int i=0;i<5;i++)
    {
        arr.push_back(i+1);
    }
    int a;
    cout<<"输入需要查找的值"<<endl;
    cin>>a;
    erfen_find(arr,a);
    return 0;
}

结果：

输入需要查找的值
3
索引：  2