基于对称最优法的BLDC转速环PI控制器设计深度解析

最新推荐文章于 2025-12-17 20:27:06 发布

原创

最新推荐文章于 2025-12-17 20:27:06 发布 · 1k 阅读

CC 4.0 BY-SA版权

文章标签：

1. 引言

直流无刷电机（BLDC）因其高功率密度、高效率等优点，在工业控制领域获得了广泛应用。其控制性能很大程度上取决于转速环的控制效果。本文将基于BLDC的dq模型，深入探讨采用对称最优法设计转速环PI参数的原理与实现方法。

我们将从BLDC的数学模型出发，分析转速环的控制结构，重点阐述对称最优法的理论基础、设计步骤和参数整定方法，并针对采样频率25kHz、电流环简化为一阶惯性环节的实际条件，提供详细的设计实例。

在dq同步旋转坐标系下，BLDC的电压方程可表示为：

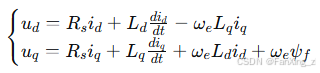
其中， $u_d$ 、 $u_q$ 为d、q轴电压， $i_d$ 、 $i_q$ 为d、q轴电流， $L_d$ 、 $L_q$ 为d、q轴电感， $R_s$ 为定子电阻， $\psi_f$ 为永磁体磁链， $\omega_e$ 为电角速度。

电磁转矩方程为：

对于面装式永磁同步电机（SPMSM）， $L_d = L_q$ ，转矩方程简化为：

其中， $K_t = \frac{3}{2} p \psi_f$ 为转矩常数， $p$ 为极对数。

转速环通常作为外环，其输出作为q轴电流的给定值 $i_q^*$ ，控制框图如下：

转速给定ω* → 转速控制器 → iq* → 电流环 → 电机 → 实际转速ω
                ↑                        |
                +------------------------+

转速控制器的设计目标是使实际转速 $\omega_m$ 快速、准确地跟踪给定值 $\omega_m^*$ ，同时保证系统的稳定性和鲁棒性。

对称最优法（Symmetrical Opt