注:本文为 “流体力学基本方程” 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
基于本科知识的流体力学基本方程推导
wuyao-hit 于 2019-08-24 20:37:08 发布
连续性方程
推导过程
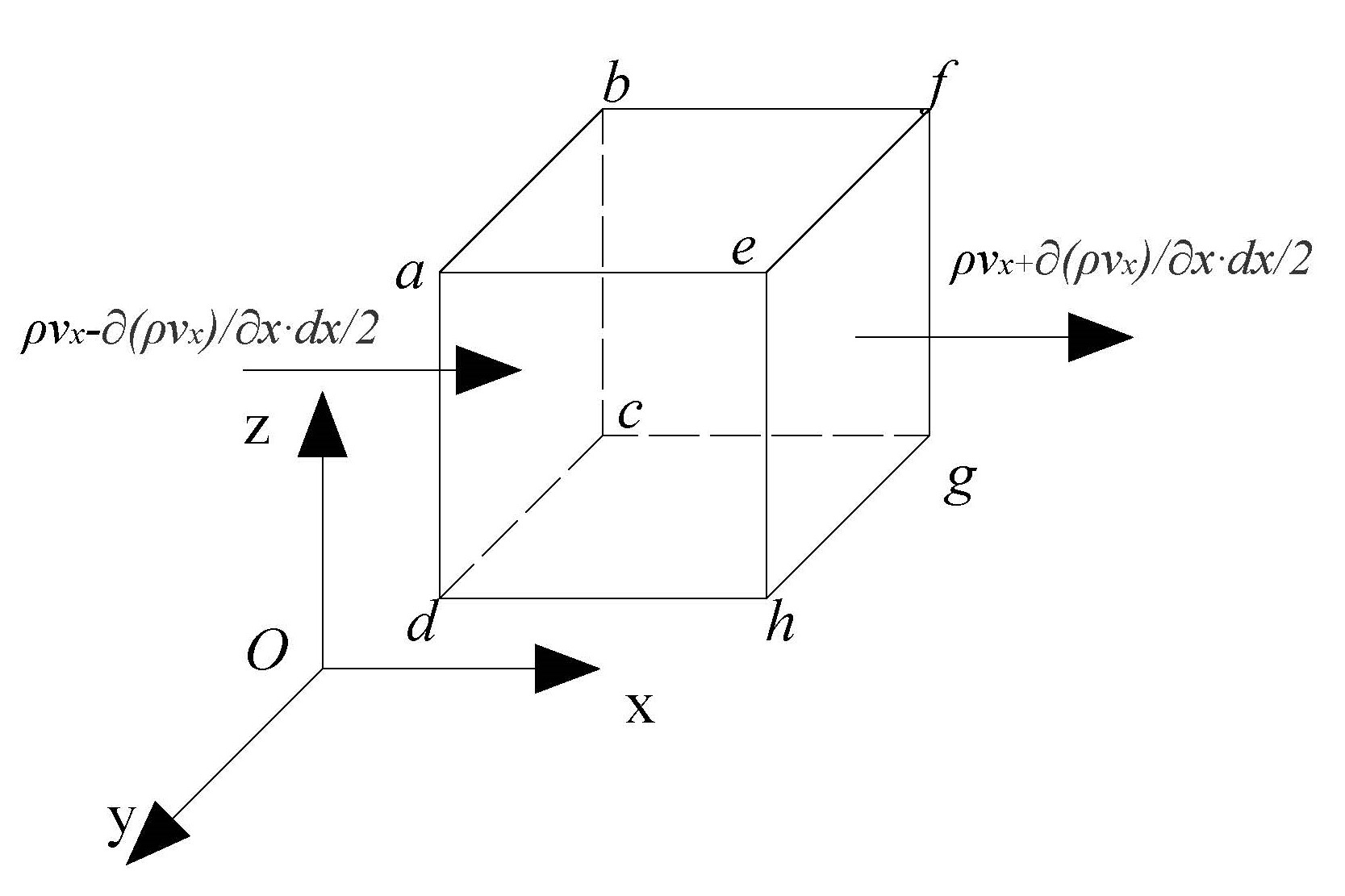
取笛卡尔坐标系下的微小控制体,分析其质量守恒关系。
-
各方向质量通量分析
-
y 方向:
t 时刻,
通过控制体左侧面 abcd 流入的质量为 [ ρ v y − 1 2 ∂ ( ρ v y ) ∂ y d y ] d x d z d t \left[ \rho v_y - \frac{1}{2} \frac{\partial (\rho v_y)}{\partial y} dy \right] dx dz dt [ρvy−21∂y∂(ρvy)dy]dxdzdt;
通过右侧面 efgh 流出的质量为 [ ρ v y + 1 2 ∂ ( ρ v y ) ∂ y d y ] d x d z d t \left[ \rho v_y + \frac{1}{2} \frac{\partial (\rho v_y)}{\partial y} dy \right] dx dz dt [ρvy+21∂y∂(ρvy)dy]dxdzdt。 -
y 方向质量损失为两者差值:
Δ m y = ∂ ( ρ v y ) ∂ y d x d y d z d t \Delta m_y = \frac{\partial (\rho v_y)}{\partial y} dx dy dz dt Δmy=∂y∂(ρvy)dxdydzdt
-
同理,
x 方向质量损失: Δ m x = ∂ ( ρ v x ) ∂ x d x d y d z d t \Delta m_x = \frac{\partial (\rho v_x)}{\partial x} dx dy dz dt Δmx=∂x∂(ρvx)dxdydzdt
z 方向质量损失: Δ m z = ∂ ( ρ v z ) ∂ z d x d y d z d t \Delta m_z = \frac{\partial (\rho v_z)}{\partial z} dx dy dz dt Δmz=∂z∂(ρvz)dxdydzdt
-
-
控制体内质量变化
控制体密度随时间变化,t 至 t+dt 时间内,密度变化 (从 ρ \rho ρ 到 ρ + ∂ ρ ∂ t d t \rho + \frac{\partial \rho}{\partial t} dt ρ+∂t∂ρdt) 引起的质量增量为 Δ m t = ∂ ρ ∂ t d x d y d z d t \Delta m_t = \frac{\partial \rho}{\partial t} dx dy dz dt Δmt=∂t∂ρdxdydzdt。 -
质量守恒方程
根据质量守恒定律,控制体内质量增量与各方向质量损失之和为零:Δ m t + ( Δ m x + Δ m y + Δ m z ) = 0 Δmt+(Δmx+Δmy+Δmz)=0 Δmt+(Δmx+Δmy+Δmz)=0,即
∂ ρ ∂ t d x d y d z d t + [ ∂ ( ρ v x ) ∂ x + ∂ ( ρ v y ) ∂ y + ∂ ( ρ v z ) ∂ z ] d x d y d z d t = 0 \frac{\partial \rho}{\partial t} dx dy dz dt + \left[ \frac{\partial (\rho v_x)}{\partial x} + \frac{\partial (\rho v_y)}{\partial y} + \frac{\partial (\rho v_z)}{\partial z} \right] dx dy dz dt = 0 ∂t∂ρdxdydzdt+[∂x∂(ρvx)+∂y∂(ρvy)+∂z∂(ρvz)]dxdydzdt=0
消去公共项 d x d y d z d t dx dy dz dt dxdydzdt,得:
∂ ρ ∂ t + ∂ ( ρ v x ) ∂ x + ∂ ( ρ v y ) ∂ y + ∂ ( ρ v z ) ∂ z = 0 (a.0.10) \frac{\partial \rho}{\partial t} + \frac{\partial (\rho v_x)}{\partial x} + \frac{\partial (\rho v_y)}{\partial y} + \frac{\partial (\rho v_z)}{\partial z} = 0 \tag{a.0.10} ∂t∂ρ+∂x∂(ρvx)+∂y∂(ρvy)+∂z∂(ρvz)=0(a.0.10)
引入散度算子 ∇ = ( ∂ ∂ x , ∂ ∂ y , ∂ ∂ z ) \nabla = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right) ∇=(∂x∂,∂y∂,∂z∂),向量形式为:
∂ ρ ∂ t + ∇ ⋅ ( ρ v ) = 0 (a.0.10a) \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho v) = 0 \tag{a.0.10a} ∂t∂ρ+∇⋅(ρv)=0(a.0.10a) -
全导数形式转换
利用物质导数定义 d ρ d t = ∂ ρ ∂ t + v x ∂ ρ ∂ x + v y ∂ ρ ∂ y + v z ∂ ρ ∂ z \frac{d \rho}{d t} = \frac{\partial \rho}{\partial t} + v_x \frac{\partial \rho}{\partial x} + v_y \frac{\partial \rho}{\partial y} + v_z \frac{\partial \rho}{\partial z} dtdρ=∂t∂ρ+vx∂x∂ρ+vy∂y∂ρ+vz∂z∂ρ,结合连续性方程可得:
d ρ d t + ρ ( ∂ v x ∂ x + ∂ v y ∂ y + ∂ v z ∂ z ) = 0 (a.0.13) \frac{d \rho}{d t} + \rho \left( \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y} + \frac{\partial v_z}{\partial z} \right) = 0 \tag{a.0.13} dtdρ+ρ(∂x∂vx+∂y∂vy+∂z∂vz)=0(a.0.13)
或改写为:
1 ρ d ρ d t + ∇ ⋅ v = 0 (a.0.13b) \frac{1}{\rho} \frac{d \rho}{d t} + \nabla \cdot v = 0 \tag{a.0.13b} ρ1dtdρ+∇⋅v=0(a.0.13b)
小结
- 式 (a.0.10) 和 (a.0.13) 为连续性方程的一般形式,适用于密度随时间和空间变化的流体。
- 恒定流动(定常流动)中,密度不随时间变化,即 ∂ ρ ∂ t = 0 \frac{\partial \rho}{\partial t} = 0 ∂t∂ρ=0,方程简化为 ∇ ⋅ ( ρ v ) = 0 \nabla \cdot (\rho v) = 0 ∇⋅(ρv)=0。
- 不可压缩流体密度为常数,方程进一步简化为 ∇ ⋅ v = 0 \nabla \cdot v = 0 ∇⋅v=0,其物理意义为空间中无质量源和汇,与散度为零的定义一致。
欧拉方程
推导依据
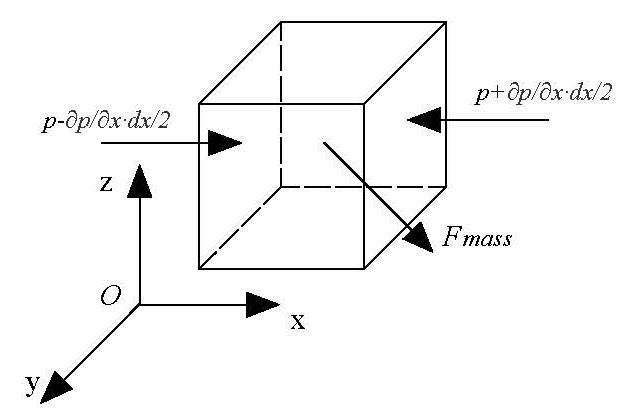
基于牛顿第二定律,针对理想流体(无粘性)建立控制体的动量平衡关系,仅考虑质量力和压力作用。
运动方程全部是基于牛顿第二定律的,因此有
表面力 + 质量力 + 达朗贝尔力 + 质量变化携带的动量变化 = 0
推导过程
-
各方向作用力分析
- 质量力:x 方向单位质量力为
f
x
f_x
fx,控制体所受质量力为
F x mass = f x ρ d x d y d z F_x^{\text{mass}} = f_x \rho dx dy dz Fxmass=fxρdxdydz - 表面力:理想流体无粘性,表面力仅为压力,且都垂直于作用面,x 方向压力合力为
F x f a c e = ( p − ∂ p ∂ x ⋅ d x 2 ) d y d z − ( p + ∂ p ∂ x ⋅ d x 2 ) d y d z = − ∂ p ∂ x d x d y d z F_x^{face} = \left( p - \frac{\partial p}{\partial x} \cdot \frac{dx}{2} \right) dy dz - \left( p + \frac{\partial p}{\partial x} \cdot \frac{dx}{2} \right) dy dz = -\frac{\partial p}{\partial x} dx dy dz Fxface=(p−∂x∂p⋅2dx)dydz−(p+∂x∂p⋅2dx)dydz=−∂x∂pdxdydz - 惯性力(达朗贝尔力):x 方向表达式为
F x D’Alembert = − ρ d x d y d z d v x d t F_x^{\text{D'Alembert}} = -\rho dx dy dz \frac{d v_x}{d t} FxD’Alembert=−ρdxdydzdtdvx - 质量变化携带的动量变化:
∂ ρ ∂ t d x d y d z ⋅ v x \frac{\partial \rho}{\partial t} dxdydz \cdot v_x ∂t∂ρdxdydz⋅vx
结合连续性方程,表达式为
− ∇ ⋅ ( ρ v ) d x d y d z ⋅ v x - \nabla \cdot (\rho v) dx dy dz \cdot v_x −∇⋅(ρv)dxdydz⋅vx
- 质量力:x 方向单位质量力为
f
x
f_x
fx,控制体所受质量力为
-
动量平衡方程
x 方向动量平衡关系为各力之和为零:
ρ f x d x d y d z − ∂ p ∂ x d x d y d z − ρ d x d y d z d v x d t − ∇ ⋅ ( ρ v ) d x d y d z ⋅ v x = 0 \rho f_x dx dy dz - \frac{\partial p}{\partial x} dx dy dz - \rho dx dy dz \frac{d v_x}{d t} - \nabla \cdot (\rho v) dx dy dz \cdot v_x = 0 ρfxdxdydz−∂x∂pdxdydz−ρdxdydzdtdvx−∇⋅(ρv)dxdydz⋅vx=0
消去公共项并扩展至 y、z 方向,得欧拉运动微分方程:
{ ρ f x − ∂ p ∂ x = ρ d v x d t + v x ∇ ⋅ ( ρ v ) ρ f y − ∂ p ∂ y = ρ d v y d t + v y ∇ ⋅ ( ρ v ) ρ f z − ∂ p ∂ z = ρ d v z d t + v z ∇ ⋅ ( ρ v ) (a.0.24) \begin{cases} \rho f_x - \frac{\partial p}{\partial x} = \rho \frac{d v_x}{d t} + v_x \nabla \cdot (\rho v) \\[1em] \rho f_y - \frac{\partial p}{\partial y} = \rho \frac{d v_y}{d t} + v_y \nabla \cdot (\rho v) \\[1em] \rho f_z - \frac{\partial p}{\partial z} = \rho \frac{d v_z}{d t} + v_z \nabla \cdot (\rho v) \end{cases} \tag{a.0.24} ⎩ ⎨ ⎧ρfx−∂x∂p=ρdtdvx+vx∇⋅(ρv)ρfy−∂y∂p=ρdtdvy+vy∇⋅(ρv)ρfz−∂z∂p=ρdtdvz+vz∇⋅(ρv)(a.0.24)
向量形式为:
ρ f − ∇ p = ρ d v d t + v ∇ ⋅ ( ρ v ) (a.0.24b) \rho f - \nabla p = \rho \frac{d v}{d t} + v \nabla \cdot (\rho v) \tag{a.0.24b} ρf−∇p=ρdtdv+v∇⋅(ρv)(a.0.24b) -
全导数展开形式
以 x 方向为例,将全导数 D v x D t \frac{D v_x}{D t} DtDvx 展开
d v x d t = ∂ v x ∂ t + v x ∂ v x ∂ x + v y ∂ v x ∂ y + v z ∂ v x ∂ z = ∂ v x ∂ t + ( v ⋅ ∇ ) v x \frac{d v_x}{d t} = \frac{\partial v_x}{\partial t} + v_x \frac{\partial v_x}{\partial x} + v_y \frac{\partial v_x}{\partial y} + v_z \frac{\partial v_x}{\partial z} = \frac{\partial v_x}{\partial t} + (v \cdot \nabla) v_x dtdvx=∂t∂vx+vx∂x∂vx+vy∂y∂vx+vz∂z∂vx=∂t∂vx+(v⋅∇)vx
其中
v
⋅
∇
=
v
x
∂
∂
x
+
v
y
∂
∂
y
+
v
z
∂
∂
z
{v} \cdot \nabla = v_x \frac{\partial}{\partial x} + v_y \frac{\partial}{\partial y} + v_z \frac{\partial}{\partial z}
v⋅∇=vx∂x∂+vy∂y∂+vz∂z∂
代入,整理得:
ρ
f
x
−
∂
p
∂
x
=
∂
(
ρ
v
x
)
∂
t
+
∇
⋅
(
ρ
v
v
x
)
(a.0.27)
\rho f_x - \frac{\partial p}{\partial x} = \frac{\partial (\rho v_x)}{\partial t} + \nabla \cdot (\rho v v_x) \tag{a.0.27}
ρfx−∂x∂p=∂t∂(ρvx)+∇⋅(ρvvx)(a.0.27)
向量形式为:
ρ
f
−
∇
p
=
ρ
∂
v
∂
t
+
∇
⋅
(
ρ
v
v
)
(a.0.27a)
\rho f - \nabla p = \rho \frac{\partial v}{\partial t} + \nabla \cdot (\rho v v) \tag{a.0.27a}
ρf−∇p=ρ∂t∂v+∇⋅(ρvv)(a.0.27a)
小结
-
式 (a.0.24) 和 (a.0.27) 为欧拉方程的一般形式,适用于密度随时空变化的理想流体。
-
不可压缩流体密度为常数且满足 ∇ ⋅ v = 0 \nabla \cdot v = 0 ∇⋅v=0,方程简化为:
f − 1 ρ ∇ p = ∂ v ∂ t + ( v ⋅ ∇ ) v (a.0.28) f - \frac{1}{\rho} \nabla p = \frac{\partial v}{\partial t} + (v \cdot \nabla) v \tag{a.0.28} f−ρ1∇p=∂t∂v+(v⋅∇)v(a.0.28) -
欧拉方程的未知数包括 ρ \rho ρ、 p p p、 f f f、 v v v,三维问题共 8 个未知量。不可压缩流体中 ρ \rho ρ 为已知常数,方程组封闭;可压缩流体需结合状态方程或能量方程实现封闭。
-
欧拉微分方程的未知数包括 ρ \rho ρ、 p p p、 f {f} f、 v {v} v,共 2 D + 2 2D+2 2D+2 个,其中 D D D 为问题的维度。以三维问题为例,3 个方程共计 8 个未知量,通常已知单位质量力为三个 f {f} f,联立连续性方程共计 ( D + 1 ) (D+1) (D+1) 个方程和 ( D + 2 ) (D+2) (D+2) 个未知量。
-
不可压缩流体
ρ \rho ρ 为已知常数,方程组封闭。 -
可压缩流体
需要建立补充方程。由于常见的可压缩流体都是气体,因此通常利用状态方程封闭方程组,也可以利用能量方程封闭。
Navier-Stokes 方程
在考虑真实流体时,由于流体具有粘性,不能简单地假设控制体积表面的所有表面力都垂直于作用面。因此,在推导不可压缩粘性流体运动方程(纳维-斯托克斯方程)时,必须将控制体积表面的切向力也纳入牛顿第二定律的考量中。
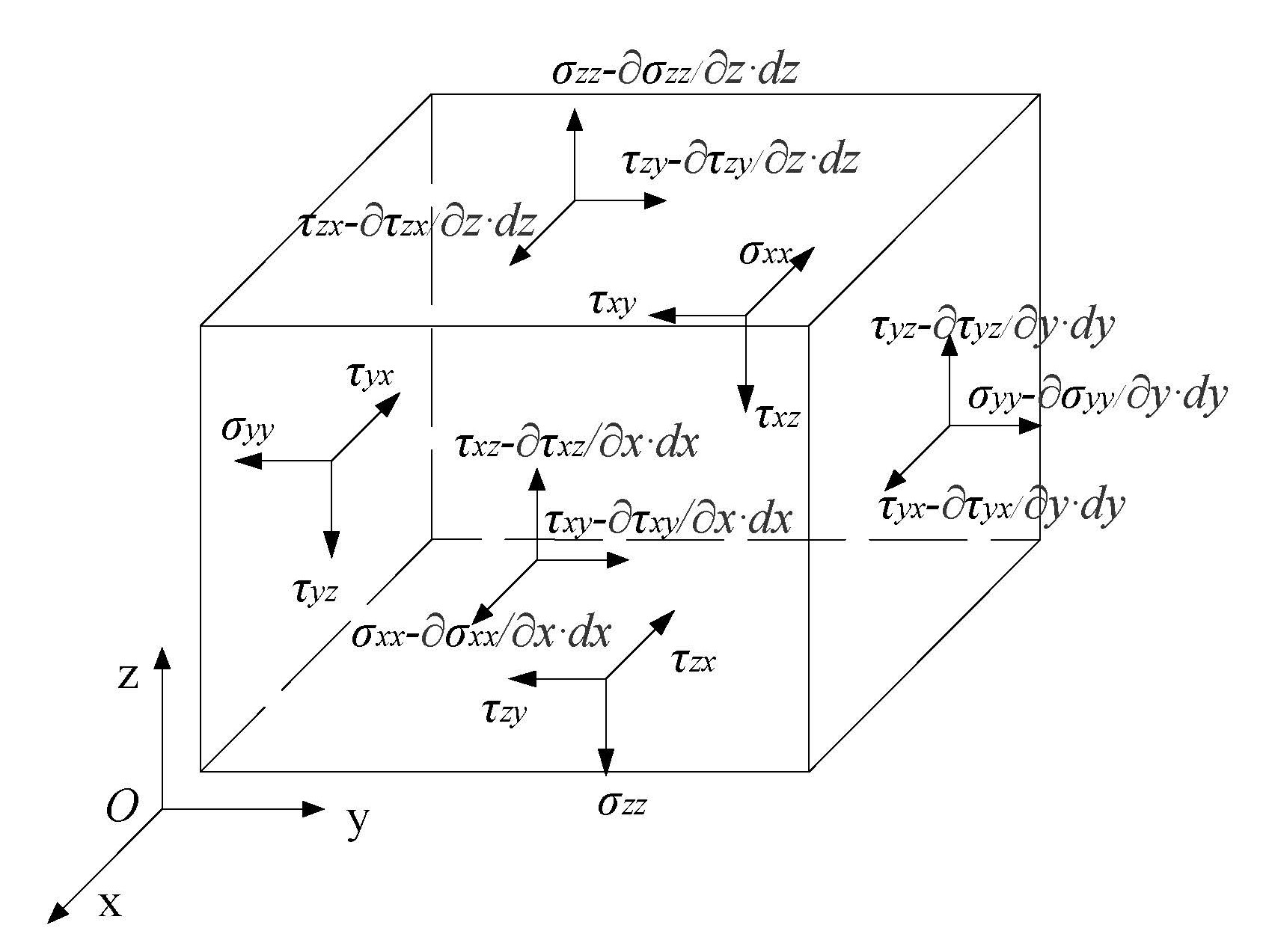
控制体积受到的表面力
应力张量与表面力
根据材料力学知识,某一点(控制体积)上的应力可表示为如下形式的应力张量:
( σ x x τ x y τ x z τ y x σ y y τ y z τ z x τ z y σ z z ) (a.0.29) \begin{pmatrix} \sigma_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \sigma_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \sigma_{zz} \end{pmatrix} \tag{a.0.29} σxxτyxτzxτxyσyyτzyτxzτyzσzz (a.0.29)
因此,该点(控制体积)单位面积上受到的净力可表示为:
( ∂ σ x x ∂ x d x + ∂ τ y x ∂ y d y + ∂ τ z x ∂ z d z ∂ τ x y ∂ x d x + ∂ σ y y ∂ y d y + ∂ τ z y ∂ z d z ∂ τ x z ∂ x d x + ∂ τ y z ∂ y d y + ∂ σ z z ∂ z d z ) (a.0.30) \begin{pmatrix} \frac{\partial \sigma_{xx}}{\partial x} dx + \frac{\partial \tau_{yx}}{\partial y} dy + \frac{\partial \tau_{zx}}{\partial z} dz \\ \frac{\partial \tau_{xy}}{\partial x} dx + \frac{\partial \sigma_{yy}}{\partial y} dy + \frac{\partial \tau_{zy}}{\partial z} dz \\ \frac{\partial \tau_{xz}}{\partial x} dx + \frac{\partial \tau_{yz}}{\partial y} dy + \frac{\partial \sigma_{zz}}{\partial z} dz \end{pmatrix} \tag{a.0.30} ∂x∂σxxdx+∂y∂τyxdy+∂z∂τzxdz∂x∂τxydx+∂y∂σyydy+∂z∂τzydz∂x∂τxzdx+∂y∂τyzdy+∂z∂σzzdz (a.0.30)
其中,每一行对应相同的作用面 d y d z dy \, dz dydz、 d x d z dx \, dz dxdz、 d x d y dx \, dy dxdy,每一列对应相同的作用方向 x x x、 y y y、 z z z。面积乘以单位面积上的力的大小,得到控制体各方向上受到表面力的大小(进行矩阵运算):
F x f a c e = ( ∂ σ x x ∂ x + ∂ τ y x ∂ y + ∂ τ z x ∂ z ) d x d y d z (a.0.31) F_x^{face} = \left( \frac{\partial \sigma_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z} \right) dx \, dy \, dz \tag{a.0.31} Fxface=(∂x∂σxx+∂y∂τyx+∂z∂τzx)dxdydz(a.0.31)
用粘性流体的表面力替换欧拉运动微分方程中的表面力项,得到粘性流体的微分运动方程:
{ ρ f x − ( ∂ σ x x ∂ x + ∂ τ y x ∂ y + ∂ τ z x ∂ z ) = ρ ∂ v x ∂ t + ∇ ⋅ ( ρ v v x ) ρ f y − ( ∂ τ x y ∂ x + ∂ σ y y ∂ y + ∂ τ z y ∂ z ) = ρ ∂ v y ∂ t + ∇ ⋅ ( ρ v v y ) ρ f z − ( ∂ τ x z ∂ x + ∂ τ y z ∂ y + ∂ σ z z ∂ z ) = ρ ∂ v z ∂ t + ∇ ⋅ ( ρ v v z ) \begin{cases} \rho f_x - \left( \frac{\partial \sigma_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z} \right) &= \rho \frac{\partial v_x}{\partial t} + \nabla \cdot (\rho v v_x) \\ \rho f_y - \left( \frac{\partial \tau_{xy}}{\partial x} + \frac{\partial \sigma_{yy}}{\partial y} + \frac{\partial \tau_{zy}}{\partial z} \right) &= \rho \frac{\partial v_y}{\partial t} + \nabla \cdot (\rho v v_y) \\ \rho f_z - \left( \frac{\partial \tau_{xz}}{\partial x} + \frac{\partial \tau_{yz}}{\partial y} + \frac{\partial \sigma_{zz}}{\partial z} \right) &= \rho \frac{\partial v_z}{\partial t} + \nabla \cdot (\rho v v_z) \end{cases} ⎩ ⎨ ⎧ρfx−(∂x∂σxx+∂y∂τyx+∂z∂τzx)ρfy−(∂x∂τxy+∂y∂σyy+∂z∂τzy)ρfz−(∂x∂τxz+∂y∂τyz+∂z∂σzz)=ρ∂t∂vx+∇⋅(ρvvx)=ρ∂t∂vy+∇⋅(ρvvy)=ρ∂t∂vz+∇⋅(ρvvz)
表面力的对称性与动量矩平衡
假设控制体积重心在 M M M 点,质量力不产生力矩,以逆时针为正方向,则表面力的力矩合为:
∑ M = τ y z d x d z d y 2 + ( τ y z + ∂ τ y z ∂ y d y ) d x d z d y 2 − τ x y d x d y d z 2 + ( τ x y − ∂ τ x y ∂ z d z ) d x d y d z 2 \sum M = \tau_{yz} dx \, dz \frac{dy}{2} + \left( \tau_{yz} + \frac{\partial \tau_{yz}}{\partial y} dy \right) dx \, dz \frac{dy}{2} - \tau_{xy} dx \, dy \frac{dz}{2} + \left( \tau_{xy} - \frac{\partial \tau_{xy}}{\partial z} dz \right) dx \, dy \frac{dz}{2} ∑M=τyzdxdz2dy+(τyz+∂y∂τyzdy)dxdz2dy−τxydxdy2dz+(τxy−∂z∂τxydz)dxdy2dz
对于控制体,转动惯量表示为:
J = ρ d x d y d z ( d r ) 2 J = \rho dx \, dy \, dz \left( dr \right)^2 J=ρdxdydz(dr)2
由动量矩平衡:
( τ y z − τ z y ) d x d y d z + ( ∂ τ y z ∂ y d y − ∂ τ z y ∂ z d z ) 1 2 d x d y d z = ρ d x d y d z ( d r ) 2 \left( \tau_{yz} - \tau_{zy} \right) dx \, dy \, dz + \left( \frac{\partial \tau_{yz}}{\partial y} dy - \frac{\partial \tau_{zy}}{\partial z} dz \right) \frac{1}{2} dx \, dy \, dz = \rho dx \, dy \, dz \left( dr \right)^2 (τyz−τzy)dxdydz+(∂y∂τyzdy−∂z∂τzydz)21dxdydz=ρdxdydz(dr)2
表面力的对称性——动量矩平衡
假设控制体重心为 M 点,质量力不产生力矩,以逆时针为正方向建立动量矩平衡方程。略去四阶和五阶小量后,可得应力分量的对称性关系:
τ
y
z
=
τ
z
y
,
τ
x
y
=
τ
y
x
,
τ
x
z
=
τ
z
x
\tau_{yz} = \tau_{zy}, \quad \tau_{xy} = \tau_{yx}, \quad \tau_{xz} = \tau_{zx}
τyz=τzy,τxy=τyx,τxz=τzx
流体中某点的应力状态可由 6 个独立分量描述(3 个正应力、3 个切应力)。即表面力可以使用 6 个独立的应力分量表示。于是假设外力项已知,对不可压缩流体
ρ
\rho
ρ 为常数,结合连续性方程共计 4 个方程,未知量包括 9 个应力,3 个速度,根据动量矩平衡可认为应力需要补充方程——即所谓的本构方程——来封闭。
牛顿内摩擦定律
实验表明,常见流体的切应力与法向速度梯度成正比,即:
τ
=
μ
d
v
d
n
\tau = \mu \frac{dv}{dn}
τ=μdndv
其中
μ
\mu
μ 为流体的动力粘度。
本构关系
切应力与角变形速度的关系(广义牛顿内摩擦定律)
将牛顿内摩擦定律推广至三维流动应用于角变形率 γ \gamma γ,得到切应力与角变形速度以下关系:
τ x y = τ y x = 2 μ γ z = μ ( ∂ v x ∂ y + ∂ v y ∂ x ) τ y z = τ z y = 2 μ γ x = μ ( ∂ v z ∂ y + ∂ v y ∂ z ) τ z x = τ x z = 2 μ γ y = μ ( ∂ v z ∂ x + ∂ v x ∂ z ) \begin{align*} \tau_{xy} &= \tau_{yx} = 2\mu \gamma_z = \mu \left( \frac{\partial v_x}{\partial y} + \frac{\partial v_y}{\partial x} \right) \\ \tau_{yz} &= \tau_{zy} = 2\mu \gamma_x = \mu \left( \frac{\partial v_z}{\partial y} + \frac{\partial v_y}{\partial z} \right) \\ \tau_{zx} &= \tau_{xz} = 2\mu \gamma_y = \mu \left( \frac{\partial v_z}{\partial x} + \frac{\partial v_x}{\partial z} \right) \end{align*} τxyτyzτzx=τyx=2μγz=μ(∂y∂vx+∂x∂vy)=τzy=2μγx=μ(∂y∂vz+∂z∂vy)=τxz=2μγy=μ(∂x∂vz+∂z∂vx)
其中:
- τ i j \tau_{ij} τij 表示第 i i i 方向和第 j j j 方向之间的剪切应力。
- μ \mu μ 是流体的动力粘度。
- v x v_x vx, v y v_y vy, v z v_z vz 分别是流体在 x x x, y y y, z z z 方向上的速度分量。
- γ z \gamma_z γz, γ x \gamma_x γx, γ y \gamma_y γy 分别是 z z z 方向、 x x x 方向和 y y y 方向的角变形率。
法向应力的本构关系
对于理想流体,法向应力与压力数值相等:
σ x x = σ y y = σ z z = − p \sigma_{xx} = \sigma_{yy} = \sigma_{zz} = -p σxx=σyy=σzz=−p
而对于粘性流体,流体微元在发生角变形的同时,也存在直线变形,在法向上引起附加法向应力,表示为:
{ σ x x = − p + σ x x ′ σ y y = − p + σ y y ′ σ z z = − p + σ z z ′ \begin{cases} \sigma_{xx} = -p + \sigma'_{xx} \\ \sigma_{yy} = -p + \sigma'_{yy} \\ \sigma_{zz} = -p + \sigma'_{zz} \end{cases} ⎩ ⎨ ⎧σxx=−p+σxx′σyy=−p+σyy′σzz=−p+σzz′
其中, p p p 表示粘性流体中的动水压强。
仿照切应变本构关系,附加法向应力等于动力粘度与线变形速度两倍的乘积:
{ σ x x ′ = μ ( ∂ v x ∂ x + ∂ v x ∂ x ) = 2 μ ∂ v x ∂ x σ y y ′ = μ ( ∂ v y ∂ y + ∂ v y ∂ y ) = 2 μ ∂ v y ∂ y σ z z ′ = μ ( ∂ v z ∂ z + ∂ v z ∂ z ) = 2 μ ∂ v z ∂ z \begin{cases} \sigma'_{xx} = \mu \left( \frac{\partial v_x}{\partial x} + \frac{\partial v_x}{\partial x} \right) = 2\mu \frac{\partial v_x}{\partial x} \\ \sigma'_{yy} = \mu \left( \frac{\partial v_y}{\partial y} + \frac{\partial v_y}{\partial y} \right) = 2\mu \frac{\partial v_y}{\partial y} \\ \sigma'_{zz} = \mu \left( \frac{\partial v_z}{\partial z} + \frac{\partial v_z}{\partial z} \right) = 2\mu \frac{\partial v_z}{\partial z} \end{cases} ⎩ ⎨ ⎧σxx′=μ(∂x∂vx+∂x∂vx)=2μ∂x∂vxσyy′=μ(∂y∂vy+∂y∂vy)=2μ∂y∂vyσzz′=μ(∂z∂vz+∂z∂vz)=2μ∂z∂vz
因此,有:
{ σ x x = − p + 2 μ ∂ v x ∂ x σ y y = − p + 2 μ ∂ v y ∂ y σ z z = − p + 2 μ ∂ v z ∂ z \begin{cases} \sigma_{xx} = -p + 2\mu \frac{\partial v_x}{\partial x} \\ \sigma_{yy} = -p + 2\mu \frac{\partial v_y}{\partial y} \\ \sigma_{zz} = -p + 2\mu \frac{\partial v_z}{\partial z} \end{cases} ⎩ ⎨ ⎧σxx=−p+2μ∂x∂vxσyy=−p+2μ∂y∂vyσzz=−p+2μ∂z∂vz
对于一种流体,其动力粘度 μ \mu μ 已知,这样上面的本构关系共补充了 6 个方程,并引入了一个新的变量——动水压强 p p p;这样对于三维不可压缩问题,共计有 10 个方程和 10 个未知量,模型得以封闭。
动水压强的物理意义
将三个方向正应力相加:
σ
x
x
+
σ
y
y
+
σ
z
z
=
−
3
p
+
2
μ
(
∂
v
x
∂
x
+
∂
v
y
∂
y
+
∂
v
z
∂
z
)
\sigma_{xx} + \sigma_{yy} + \sigma_{zz} = -3p + 2\mu \left( \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y} + \frac{\partial v_z}{\partial z} \right)
σxx+σyy+σzz=−3p+2μ(∂x∂vx+∂y∂vy+∂z∂vz)
不可压缩流体满足
∇
⋅
v
=
0
\nabla \cdot v = 0
∇⋅v=0,等式右边第二项为零,因此
p
=
−
1
3
(
σ
x
x
+
σ
y
y
+
σ
z
z
)
p = -\frac{1}{3}(\sigma_{xx} + \sigma_{yy} + \sigma_{zz})
p=−31(σxx+σyy+σzz),即动水压强为空间法向应力的平均值。
三个方向上的正应力相加得到
σ x x + σ y y + σ z z = − 3 p + 2 μ ( ∂ v x ∂ x + ∂ v y ∂ y + ∂ v z ∂ z ) \sigma_{xx} + \sigma_{yy} + \sigma_{zz} = -3p + 2\mu \left( \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y} + \frac{\partial v_z}{\partial z} \right) σxx+σyy+σzz=−3p+2μ(∂x∂vx+∂y∂vy+∂z∂vz)
对于不可压缩流体,等式右边第二项为零,即
p = − σ x x + σ y y + σ z z 3 p = -\frac{\sigma_{xx} + \sigma_{yy} + \sigma_{zz}}{3} p=−3σxx+σyy+σzz
说明动水压强的含义为空间法向应力的平均值。
Navier-Stokes方程
整理合并上面的方程,得到
ρ f x − { ∂ ∂ x [ − p + 2 μ ∂ v x ∂ x ] + ∂ ∂ y [ μ ( ∂ v x ∂ y + ∂ v y ∂ x ) ] + ∂ ∂ z [ μ ( ∂ v x ∂ z + ∂ v z ∂ x ) ] } = ρ ∂ v x ∂ t + ∇ ⋅ ( ρ v v x ) \rho f_x - \left\{ \frac{\partial}{\partial x} \left[ -p + 2\mu \frac{\partial v_x}{\partial x} \right] + \frac{\partial}{\partial y} \left[ \mu \left( \frac{\partial v_x}{\partial y} + \frac{\partial v_y}{\partial x} \right) \right] + \frac{\partial}{\partial z} \left[ \mu \left( \frac{\partial v_x}{\partial z} + \frac{\partial v_z}{\partial x} \right) \right] \right\} = \rho \frac{\partial v_x}{\partial t} + \nabla \cdot (\rho v v_x) ρfx−{∂x∂[−p+2μ∂x∂vx]+∂y∂[μ(∂y∂vx+∂x∂vy)]+∂z∂[μ(∂z∂vx+∂x∂vz)]}=ρ∂t∂vx+∇⋅(ρvvx)
若粘度不变(常物性),则有
ρ f x − { − ∂ p ∂ x + 2 μ ∂ 2 v x ∂ x 2 + μ ∂ v x 2 ∂ y 2 + μ ∂ v x 2 ∂ z 2 + μ ∂ v y ∂ x ∂ y + μ ∂ v z ∂ x ∂ z } = ρ ∂ v x ∂ t + ∇ ⋅ ( ρ v v x ) ρ f y − ∂ p ∂ y − μ { ∂ v x 2 ∂ x 2 + ∂ v y 2 ∂ y 2 + ∂ v z 2 ∂ z 2 } + ∂ ∂ x [ ∂ v x ∂ y + ∂ v y ∂ x ] + ∂ ∂ z [ ∂ v y ∂ z + ∂ v z ∂ y ] = ρ ∂ v y ∂ t + ∇ ⋅ ( ρ v v y ) ρ f z − ∂ p ∂ z − μ [ ∇ 2 v z + ∇ x ⋅ ( ∇ x ⋅ v ) ] = ρ ∂ v z ∂ t + ∇ ⋅ ( ρ v v z ) \begin{align*} \rho f_x - \left\{ -\frac{\partial p}{\partial x} + 2\mu \frac{\partial^2 v_x}{\partial x^2} + \mu \frac{\partial v_x^2}{\partial y^2} + \mu \frac{\partial v_x^2}{\partial z^2} + \mu \frac{\partial v_y}{\partial x \partial y} + \mu \frac{\partial v_z}{\partial x \partial z} \right\} &= \rho \frac{\partial v_x}{\partial t} + \nabla \cdot (\rho v v_x) \\ \rho f_y - \frac{\partial p}{\partial y} - \mu \left\{ \frac{\partial v_x^2}{\partial x^2} + \frac{\partial v_y^2}{\partial y^2} + \frac{\partial v_z^2}{\partial z^2} \right\} + \frac{\partial}{\partial x} \left[ \frac{\partial v_x}{\partial y} + \frac{\partial v_y}{\partial x} \right] + \frac{\partial}{\partial z} \left[ \frac{\partial v_y}{\partial z} + \frac{\partial v_z}{\partial y} \right] &= \rho \frac{\partial v_y}{\partial t} + \nabla \cdot (\rho v v_y) \\ \rho f_z - \frac{\partial p}{\partial z} - \mu \left[ \nabla^2 v_z + \nabla_x \cdot (\nabla_x \cdot v) \right] &= \rho \frac{\partial v_z}{\partial t} + \nabla \cdot (\rho v v_z) \end{align*} ρfx−{−∂x∂p+2μ∂x2∂2vx+μ∂y2∂vx2+μ∂z2∂vx2+μ∂x∂y∂vy+μ∂x∂z∂vz}ρfy−∂y∂p−μ{∂x2∂vx2+∂y2∂vy2+∂z2∂vz2}+∂x∂[∂y∂vx+∂x∂vy]+∂z∂[∂z∂vy+∂y∂vz]ρfz−∂z∂p−μ[∇2vz+∇x⋅(∇x⋅v)]=ρ∂t∂vx+∇⋅(ρvvx)=ρ∂t∂vy+∇⋅(ρvvy)=ρ∂t∂vz+∇⋅(ρvvz)
Navier-Stokes 方程的最终形式
将本构关系代入粘性流体微分运动方程,假设流体为常物性(粘度
μ
\mu
μ 不变),结合不可压缩流体连续性方程
∇
⋅
v
=
0
\nabla \cdot v = 0
∇⋅v=0,化简得到 Navier-Stokes 方程(不可压缩粘性流体运动方程):
{
f
x
−
1
ρ
∂
p
∂
x
+
ν
∇
2
v
x
=
∂
v
x
∂
t
+
(
v
⋅
∇
)
v
x
f
y
−
1
ρ
∂
p
∂
y
+
ν
∇
2
v
y
=
∂
v
y
∂
t
+
(
v
⋅
∇
)
v
y
f
z
−
1
ρ
∂
p
∂
z
+
ν
∇
2
v
z
=
∂
v
z
∂
t
+
(
v
⋅
∇
)
v
z
\begin{cases} f_x - \frac{1}{\rho} \frac{\partial p}{\partial x} + \nu \nabla^2 v_x = \frac{\partial v_x}{\partial t} + (v \cdot \nabla) v_x \\ f_y - \frac{1}{\rho} \frac{\partial p}{\partial y} + \nu \nabla^2 v_y = \frac{\partial v_y}{\partial t} + (v \cdot \nabla) v_y \\ f_z - \frac{1}{\rho} \frac{\partial p}{\partial z} + \nu \nabla^2 v_z = \frac{\partial v_z}{\partial t} + (v \cdot \nabla) v_z \end{cases}
⎩
⎨
⎧fx−ρ1∂x∂p+ν∇2vx=∂t∂vx+(v⋅∇)vxfy−ρ1∂y∂p+ν∇2vy=∂t∂vy+(v⋅∇)vyfz−ρ1∂z∂p+ν∇2vz=∂t∂vz+(v⋅∇)vz
其中
ν
=
μ
ρ
\nu = \frac{\mu}{\rho}
ν=ρμ 为运动粘度,
∇
2
=
∂
2
∂
x
2
+
∂
2
∂
y
2
+
∂
2
∂
z
2
\nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}
∇2=∂x2∂2+∂y2∂2+∂z2∂2 为拉普拉斯算子。向量形式为:
f
−
1
ρ
∇
p
+
ν
∇
2
v
=
∂
v
∂
t
+
(
v
⋅
∇
)
v
f - \frac{1}{\rho} \nabla p + \nu \nabla^2 v = \frac{\partial v}{\partial t} + (v \cdot \nabla) v
f−ρ1∇p+ν∇2v=∂t∂v+(v⋅∇)v
计算流体力学 1 -流体力学的控制方程
mw_1422102031 原创已于 2022-10-19 12:44:57 修改
前言
只是为方便学习,不做其他用途
学堂在线配套视频网址:
https://www.xuetangx.com/learn/nwpuP0401KC007315/nwpuP0401KC007315/14070335/video/24702135
一、流动控制方程的推导及其物理含义的讨论、适用于 CFD 计算的控制方程形式
1.1 引言




1.2 流动模型








1.3 实质导数



对于函数ρ,我们可以在位置点 1,时刻 t1 进行 Talor 级数展开,得到ρ 2 ρ_2ρ2 的近似表达式:








1.4 速度的散度及其物理意义




1.5 连续方程


1.5.1 基于固定于空间的有限控制体模型的连续方程推导 (守恒型积分方程的推导)





1.5.2 基于随流体运动有限控制体模型的连续方程推导 (非守恒型积分方程的推导)


1.5.3 基于固定于空间的无限小流体微元模型的连续方程推导 (守恒型偏微分方程)






1.5.4 基于随流体运动无限小流体微元模型的连续方程推导 (非守恒型偏微分方程)




1.6 动量方程

















1.7 能量方程




















1.10 适合计算流体力学的控制方程形式























计算流体力学 2 - 偏微分方程的数学性质对 CFD 的影响
mw_1422102031 原创已于 2022-10-25 22:35:04 修改・
前言
接前文 [计算流体力学 1]
课程来自学堂在线的 计算流体力学
一、偏微分方程的数学性质对 CFD 的影响
1.1 引言



1.2 准线性偏微分方程的分类



整理后可得:













1.3 偏微分方程组的一般分类方法:特征值方法


















1.4 不同类型偏微分方程的一般性质、物理含义及其对 CFD 计算方法的影响














3.5 适定问题


3.6 补充:计算流体力学中不同类型的常用模型方程及其特性












课后习题:


二、偏微分方程的离散

2.1 绪论


2.2 有限差分基础






一阶前差、一阶后差和中心差分的几何意义示意图 :


二阶导数的差分算子:






2.3 偏微分方程的差分方程








2.4 显示方法和隐式方法









2.5 误差与稳定性分析























流体力学-----连续性方程的推导和理解
mw_1422102031 原创已于 2023-04-08 10:31:53 修改
前言



连续性方程的推导和理解



积分方程和微分方程的比较



- 流体力学基本方程(篇 1)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/155062256
via:
- 使用本科知识进行流体力学基本方程推导_流体通量公式-优快云博客
https://blog.youkuaiyun.com/weixin_45564064/article/details/100056809 - 计算流体力学 1-流体力学的控制方程_将积分形式的流体力学控制方程写成单一的通用形式-优快云博客
https://blog.youkuaiyun.com/mw_1422102031/article/details/127261808 - 计算流体力学 2-偏微分方程的数学性质对CFD的影响_偏微分方程的数学性质对 cfd 的影响-优快云博客
https://blog.youkuaiyun.com/mw_1422102031/article/details/127432734 - 流体力学-----连续性方程的推导和理解_连续性方程推导-优快云博客
https://blog.youkuaiyun.com/mw_1422102031/article/details/130006516





















 1356
1356

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








