注:本文为 “Lambert W 函数” 相关合辑。
略作重排,未校未去重。
如有内容异常,请看原文。
导数压轴题“隐零点”的处理策略
Dylaaan 发布于 发布于 2019-02-23 19:23・北京
在利用导数研究函数的最大值与最小值时,常需确定导函数的零点。
例如,若要求解函数 f ( x ) = e x − x f(x)=e^x - x f(x)=ex−x 的最小值,可先求解其导函数的零点。
该函数的导函数为 f ′ ( x ) = e x − 1 f'(x)=e^x - 1 f′(x)=ex−1,易知 x = 0 x = 0 x=0 是其导函数的唯一零点(即函数 f ( x ) f(x) f(x) 的极值点)。
进一步分析可得,函数 f ( x ) f(x) f(x) 在区间 ( − ∞ , 0 ) (-\infty,0) (−∞,0) 上单调递减,在区间 ( 0 , + ∞ ) (0,+\infty) (0,+∞) 上单调递增。
因此,函数的最小值为 f ( x ) min = f ( 0 ) = 1 f(x)_{\text{min}}=f(0)=1 f(x)min=f(0)=1,此即为所求结果。
但在部分情形下,导函数的零点难以直接求解,例如如下函数:
设函数 f ( x ) = e x − ln x f(x)=e^x - \ln x f(x)=ex−lnx,其导函数为 f ′ ( x ) = e x − 1 x f'(x)=e^x - \frac{1}{x} f′(x)=ex−x1。易知导函数 f ′ ( x ) f'(x) f′(x) 在区间 ( 0 , + ∞ ) (0,+\infty) (0,+∞) 上单调递增,且满足 f ′ ( 1 2 ) = e − 2 < 0 f'(\frac{1}{2})=\sqrt{e} - 2 < 0 f′(21)=e−2<0, f ′ ( 1 ) = e − 1 > 0 f'(1)=e - 1 > 0 f′(1)=e−1>0。
根据零点定理可知,存在 x 0 ∈ ( 1 2 , 1 ) x_0 \in (\frac{1}{2},1) x0∈(21,1),使得 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0。
结合导函数 f ′ ( x ) f'(x) f′(x) 的单调性可推得,函数 f ( x ) f(x) f(x) 在区间 ( 0 , x 0 ) (0,x_0) (0,x0) 上单调递减,在区间 ( x 0 , + ∞ ) (x_0,+\infty) (x0,+∞) 上单调递增。
然而,此处 x 0 x_0 x0 的具体数值无法通过简单的数值形式表示。
实际上,借助计算器可求得 x 0 ≈ 0.56714 ⋯ x_0 \approx 0.56714\cdots x0≈0.56714⋯。
若直接计算 f ( 0.56714 ⋯ ) f(0.56714\cdots) f(0.56714⋯) 的值,计算难度较大。因此,需寻找更适宜的方法以计算(或估计) f ( x 0 ) f(x_0) f(x0) 的值。
所谓“隐零点”
“隐零点”即指上述情形:需利用方程 x 0 e x 0 = 1 x_0 e^{x_0}=1 x0ex0=1 的解,但无法直接求解该方程。此时,需通过“代入”的方法进行处理。
以函数 f ( x ) = e x − ln x f(x)=e^x - \ln x f(x)=ex−lnx 为例,其极值点 x 0 x_0 x0 满足 x 0 e x 0 = 1 x_0 e^{x_0}=1 x0ex0=1,且 x 0 ∈ ( 1 2 , 1 ) x_0 \in (\frac{1}{2},1) x0∈(21,1)。
由 x 0 e x 0 = 1 x_0 e^{x_0}=1 x0ex0=1 可推得 e x 0 = 1 x 0 e^{x_0}=\frac{1}{x_0} ex0=x01,同时 x 0 e x 0 = 1 ⇔ x 0 + ln x 0 = 0 x_0 e^{x_0}=1 \Leftrightarrow x_0 + \ln x_0=0 x0ex0=1⇔x0+lnx0=0,即 ln x 0 = − x 0 \ln x_0=-x_0 lnx0=−x0。
因此, f ( x 0 ) = x 0 + 1 x 0 > 2 f(x_0)=x_0 + \frac{1}{x_0} > 2 f(x0)=x0+x01>2,由此可对函数 f ( x ) f(x) f(x) 的最小值进行估计。
(事实上,该方程的解与“朗伯函数”存在关联。)
下文将讨论两种不同的“隐零点”处理方式。
方式一:代入变量
“代入变量”即消去变量 x x x,此为处理不含参数问题的常用方法。
以下从证明一个不等式展开讨论:
例 1
当 x > 0 x > 0 x>0 时,证明: x e x ≥ x + ln x + 1 x e^x \geq x + \ln x + 1 xex≥x+lnx+1。
证明:设函数 f ( x ) = x e x − x − ln x − 1 f(x)=x e^x - x - \ln x - 1 f(x)=xex−x−lnx−1,其导函数为 f ′ ( x ) = ( x + 1 ) ( e x − 1 x ) f'(x)=(x + 1)(e^x - \frac{1}{x}) f′(x)=(x+1)(ex−x1)。
由于 x + 1 > 0 x + 1 > 0 x+1>0( x > 0 x > 0 x>0),设 g ( x ) = e x − 1 x g(x)=e^x - \frac{1}{x} g(x)=ex−x1,显然函数 g ( x ) g(x) g(x) 在区间 ( 0 , + ∞ ) (0,+\infty) (0,+∞) 上单调递增。
又 g ( 1 2 ) = e − 2 < 0 g(\frac{1}{2})=\sqrt{e} - 2 < 0 g(21)=e−2<0, g ( 1 ) = e − 1 > 0 g(1)=e - 1 > 0 g(1)=e−1>0,根据零点定理可知,存在 x 0 ∈ ( 1 2 , 1 ) x_0 \in (\frac{1}{2},1) x0∈(21,1),使得 g ( x 0 ) = 0 g(x_0)=0 g(x0)=0。
由 g ( x 0 ) = 0 g(x_0)=0 g(x0)=0 可推得 e x 0 = 1 x 0 e^{x_0}=\frac{1}{x_0} ex0=x01,进一步可得 ln x 0 = − x 0 \ln x_0=-x_0 lnx0=−x0。
结合导函数的符号可判断,函数 f ( x ) f(x) f(x) 在区间 ( 0 , x 0 ) (0,x_0) (0,x0) 上单调递减,在区间 ( x 0 , + ∞ ) (x_0,+\infty) (x0,+∞) 上单调递增。
因此,函数
f
(
x
)
f(x)
f(x) 的最小值为:
f
(
x
)
min
=
f
(
x
0
)
=
x
0
e
x
0
−
x
0
−
ln
x
0
−
1
=
1
−
x
0
+
x
0
−
1
=
0
\begin{align*} f(x)_{\text{min}}&=f(x_0)\\ &=x_0 e^{x_0} - x_0 - \ln x_0 - 1\\ &=1 - x_0 + x_0 - 1\\ &=0 \end{align*}
f(x)min=f(x0)=x0ex0−x0−lnx0−1=1−x0+x0−1=0
故
f
(
x
)
≥
0
f(x) \geq 0
f(x)≥0,原不等式得证。
此处再次应用了方程 x 0 e x 0 = 1 x_0 e^{x_0}=1 x0ex0=1 的关系。
例 2
下述题目为 2017 年全国Ⅱ卷数学压轴题:
已知函数 f ( x ) = a x 2 − a x − x ln x f(x)=a x^2 - a x - x \ln x f(x)=ax2−ax−xlnx,且 f ( x ) ≥ 0 f(x) \geq 0 f(x)≥0 恒成立。
(1)求实数 a a a 的值;
(2)证明:函数 f ( x ) f(x) f(x) 存在唯一的极大值点 x 0 x_0 x0,且 e − 2 < f ( x 0 ) < 2 − 2 e^{-2} < f(x_0) < 2^{-2} e−2<f(x0)<2−2。
分析:第(1)问可解得 a = 1 a = 1 a=1,此问求解过程较为基础,此处不展开论述,可参考相关解析资料。第(2)问需应用上述“隐零点”方法,并估计极大值的取值范围。
证明:由(1)知 f ( x ) = x 2 − x − x ln x f(x)=x^2 - x - x \ln x f(x)=x2−x−xlnx,其导函数为 f ′ ( x ) = 2 x − 2 − ln x f'(x)=2x - 2 - \ln x f′(x)=2x−2−lnx。
函数 f ′ ( x ) f'(x) f′(x) 的二阶导函数为 f ′ ′ ( x ) = 2 − 1 x f''(x)=2 - \frac{1}{x} f′′(x)=2−x1,因此导函数 f ′ ( x ) f'(x) f′(x) 在区间 ( 0 , 1 2 ) (0,\frac{1}{2}) (0,21) 上单调递减,在区间 ( 1 2 , + ∞ ) (\frac{1}{2},+\infty) (21,+∞) 上单调递增。
又 f ′ ( e − 2 ) = 2 e − 2 > 0 f'(e^{-2})=2e^{-2} > 0 f′(e−2)=2e−2>0, f ′ ( 1 2 ) = ln 2 − 1 < 0 f'(\frac{1}{2})=\ln 2 - 1 < 0 f′(21)=ln2−1<0, f ′ ( 1 ) = 0 f'(1)=0 f′(1)=0,根据零点定理可知,存在 x 0 ∈ ( e − 2 , 1 2 ) x_0 \in (e^{-2},\frac{1}{2}) x0∈(e−2,21),使得 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0。
由 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0 可推得 ln x 0 = 2 x 0 − 2 \ln x_0=2x_0 - 2 lnx0=2x0−2,此时易知 x = x 0 x = x_0 x=x0 是函数 f ( x ) f(x) f(x) 的极大值点。
计算极大值
f
(
x
0
)
f(x_0)
f(x0):
f
(
x
0
)
=
x
0
2
−
x
0
−
x
0
ln
x
0
=
x
0
2
−
x
0
−
x
0
(
2
x
0
−
2
)
=
x
0
(
1
−
x
0
)
\begin{align*} f(x_0)&=x_0^2 - x_0 - x_0 \ln x_0\\ &=x_0^2 - x_0 - x_0(2x_0 - 2)\\ &=x_0(1 - x_0) \end{align*}
f(x0)=x02−x0−x0lnx0=x02−x0−x0(2x0−2)=x0(1−x0)
由基本不等式可得
x
0
(
1
−
x
0
)
<
(
x
0
+
1
−
x
0
2
)
2
=
2
−
2
x_0(1 - x_0) < (\frac{x_0 + 1 - x_0}{2})^2=2^{-2}
x0(1−x0)<(2x0+1−x0)2=2−2。
另一方面,由于 e − 1 ∈ ( 0 , 1 2 ) e^{-1} \in (0,\frac{1}{2}) e−1∈(0,21),且函数在区间 ( e − 2 , x 0 ) (e^{-2},x_0) (e−2,x0) 上单调递增,故极大值 f ( x 0 ) > f ( e − 1 ) = e − 2 f(x_0) > f(e^{-1})=e^{-2} f(x0)>f(e−1)=e−2。
综上,极大值 f ( x 0 ) f(x_0) f(x0) 满足 e − 2 < f ( x 0 ) < 2 − 2 e^{-2} < f(x_0) < 2^{-2} e−2<f(x0)<2−2,原命题得证。
方式二:代入参数
“代入参数”的方法通常用于处理含参数的函数问题。
例 3
已知函数 f ( x ) = 2 e x − ( x + a ) 2 f(x)=2e^x - (x + a)^2 f(x)=2ex−(x+a)2,若当 x ≥ 0 x \geq 0 x≥0 时,不等式 f ( x ) ≥ 0 f(x) \geq 0 f(x)≥0 恒成立,求实数 a a a 的取值范围。
解答:函数 f ( x ) f(x) f(x) 的导函数为 f ′ ( x ) = 2 ( e x − x − a ) f'(x)=2(e^x - x - a) f′(x)=2(ex−x−a),其二阶导函数为 f ′ ′ ( x ) = 2 ( e x − 1 ) ≥ 0 f''(x)=2(e^x - 1) \geq 0 f′′(x)=2(ex−1)≥0( x ≥ 0 x \geq 0 x≥0)。
因此,导函数 f ′ ( x ) f'(x) f′(x) 在区间 [ 0 , + ∞ ) [0,+\infty) [0,+∞) 上单调递增,且 f ′ ( 0 ) = 2 ( 1 − a ) f'(0)=2(1 - a) f′(0)=2(1−a),据此分情况讨论:
-
当 a ≤ 1 a \leq 1 a≤1 时, f ′ ( x ) ≥ f ′ ( 0 ) = 2 ( 1 − a ) ≥ 0 f'(x) \geq f'(0)=2(1 - a) \geq 0 f′(x)≥f′(0)=2(1−a)≥0,故函数 f ( x ) f(x) f(x) 在区间 [ 0 , + ∞ ) [0,+\infty) [0,+∞) 上单调递增。
此时需满足 f ( 0 ) = 2 − a 2 ≥ 0 f(0)=2 - a^2 \geq 0 f(0)=2−a2≥0,解得 a ∈ [ − 2 , 1 ] a \in [-\sqrt{2},1] a∈[−2,1]。
-
当 a > 1 a > 1 a>1 时, f ′ ( 0 ) < 0 f'(0) < 0 f′(0)<0,又 f ′ ( a ) = 2 ( e a − 2 a ) > 0 f'(a)=2(e^a - 2a) > 0 f′(a)=2(ea−2a)>0(此处应用不等式 e x ≥ e x e^x \geq e x ex≥ex, x ∈ R x \in \mathbb{R} x∈R)。
根据零点定理可知,存在 x 0 ∈ [ 0 , a ] x_0 \in [0,a] x0∈[0,a],使得 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0,由 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0 可推得 a = e x 0 − x 0 a=e^{x_0} - x_0 a=ex0−x0。
结合导函数的符号可判断,函数 f ( x ) f(x) f(x) 在区间 [ 0 , x 0 ) [0,x_0) [0,x0) 上单调递减,在区间 ( x 0 , + ∞ ) (x_0,+\infty) (x0,+∞) 上单调递增。
因此,函数 f ( x ) f(x) f(x) 的最小值为 f ( x 0 ) = 2 e x 0 − e 2 x 0 = e x 0 ( 2 − e x 0 ) f(x_0)=2e^{x_0} - e^{2x_0}=e^{x_0}(2 - e^{x_0}) f(x0)=2ex0−e2x0=ex0(2−ex0),需满足 f ( x 0 ) ≥ 0 f(x_0) \geq 0 f(x0)≥0。
由 e x 0 ( 2 − e x 0 ) ≥ 0 e^{x_0}(2 - e^{x_0}) \geq 0 ex0(2−ex0)≥0 可推得 e x 0 ≤ 2 e^{x_0} \leq 2 ex0≤2,解得 x 0 ∈ ( 0 , ln 2 ] x_0 \in (0,\ln 2] x0∈(0,ln2],进而可得 a = e x 0 − x 0 ∈ ( 1 , 2 − ln 2 ] a=e^{x_0} - x_0 \in (1,2 - \ln 2] a=ex0−x0∈(1,2−ln2]。
综上,实数 a a a 的取值范围为 [ − 2 , 2 − ln 2 ] [-\sqrt{2},2 - \ln 2] [−2,2−ln2]。
例 4
已知函数 f ( x ) = x + 1 x − 2 f(x)=x + \frac{1}{x} - 2 f(x)=x+x1−2。
(1)求证: f ( x ) ≤ ( x − 1 x ) ln x f(x) \leq (x - \frac{1}{x})\ln x f(x)≤(x−x1)lnx;
(2)若关于 x x x 的不等式 f ( x ) ≥ a ln x + 2 e − 2 f(x) \geq a \ln x + \frac{2}{e} - 2 f(x)≥alnx+e2−2 恒成立,求实数 a a a 的取值范围。
解答:
(1)设函数 g ( x ) = f ( x ) − ( x − 1 x ) ln x g(x)=f(x) - (x - \frac{1}{x})\ln x g(x)=f(x)−(x−x1)lnx,其导函数为 g ′ ( x ) = − ( 1 + 1 x 2 ) ln x g'(x)=-(1 + \frac{1}{x^2})\ln x g′(x)=−(1+x21)lnx。
根据导函数的符号可判断,函数 g ( x ) g(x) g(x) 在区间 ( 0 , 1 ) (0,1) (0,1) 上单调递增,在区间 ( 1 , + ∞ ) (1,+\infty) (1,+∞) 上单调递减。
因此, g ( x ) ≤ g ( 1 ) = 0 g(x) \leq g(1)=0 g(x)≤g(1)=0,即 f ( x ) ≤ ( x − 1 x ) ln x f(x) \leq (x - \frac{1}{x})\ln x f(x)≤(x−x1)lnx,原不等式得证。
(2)设函数 h ( x ) = f ( x ) − a ln x − 2 e + 2 = x + 1 x − a ln x − 2 e h(x)=f(x) - a \ln x - \frac{2}{e} + 2=x + \frac{1}{x} - a \ln x - \frac{2}{e} h(x)=f(x)−alnx−e2+2=x+x1−alnx−e2,其导函数为 h ′ ( x ) = x 2 − a x − 1 x 2 h'(x)=\frac{x^2 - a x - 1}{x^2} h′(x)=x2x2−ax−1。
考虑函数 m ( x ) = x 2 − a x − 1 m(x)=x^2 - a x - 1 m(x)=x2−ax−1,由于 m ( 0 ) = − 1 < 0 m(0)=-1 < 0 m(0)=−1<0,根据零点定理可知,存在 x 0 ∈ ( 0 , + ∞ ) x_0 \in (0,+\infty) x0∈(0,+∞),使得 m ( x 0 ) = 0 m(x_0)=0 m(x0)=0。
由 m ( x 0 ) = 0 m(x_0)=0 m(x0)=0 可推得 x 0 2 − a x 0 − 1 = 0 x_0^2 - a x_0 - 1=0 x02−ax0−1=0,即 a = x 0 − 1 x 0 a=x_0 - \frac{1}{x_0} a=x0−x01。
结合导函数的符号可判断,函数 h ( x ) h(x) h(x) 在区间 ( 0 , x 0 ) (0,x_0) (0,x0) 上单调递减,在区间 ( x 0 , + ∞ ) (x_0,+\infty) (x0,+∞) 上单调递增。
因此,函数
h
(
x
)
h(x)
h(x) 的最小值为:
h
(
x
0
)
=
x
0
+
1
x
0
−
a
ln
x
0
−
2
e
=
x
0
+
1
x
0
−
(
x
0
−
1
x
0
)
ln
x
0
−
2
e
\begin{align*} h(x_0)&=x_0 + \frac{1}{x_0} - a \ln x_0 - \frac{2}{e}\\ &=x_0 + \frac{1}{x_0} - (x_0 - \frac{1}{x_0})\ln x_0 - \frac{2}{e} \end{align*}
h(x0)=x0+x01−alnx0−e2=x0+x01−(x0−x01)lnx0−e2
设
φ
(
x
)
=
x
+
1
x
−
(
x
−
1
x
)
ln
x
−
2
e
\varphi(x)=x + \frac{1}{x} - (x - \frac{1}{x})\ln x - \frac{2}{e}
φ(x)=x+x1−(x−x1)lnx−e2,由(1)可知,函数
φ
(
x
)
\varphi(x)
φ(x) 在区间
(
0
,
1
)
(0,1)
(0,1) 上单调递增,在区间
(
1
,
+
∞
)
(1,+\infty)
(1,+∞) 上单调递减,且
φ
(
1
)
=
2
−
2
e
>
0
\varphi(1)=2 - \frac{2}{e} > 0
φ(1)=2−e2>0。
注意到 φ ( 1 e ) = φ ( e ) = 0 \varphi(\frac{1}{e})=\varphi(e)=0 φ(e1)=φ(e)=0,若 h ( x 0 ) ≥ 0 h(x_0) \geq 0 h(x0)≥0,则需满足 x 0 ∈ [ 1 e , e ] x_0 \in [\frac{1}{e},e] x0∈[e1,e]。
又 a = x 0 − 1 x 0 a=x_0 - \frac{1}{x_0} a=x0−x01 在区间 [ 1 e , e ] [\frac{1}{e},e] [e1,e] 上单调递增,故 a ∈ [ 1 e − e , e − 1 e ] a \in [\frac{1}{e} - e,e - \frac{1}{e}] a∈[e1−e,e−e1]。
因此,实数 a a a 的取值范围为 [ 1 e − e , e − 1 e ] [\frac{1}{e} - e,e - \frac{1}{e}] [e1−e,e−e1]。
编辑于 2025-08-29 22:22・北京
朗博函数与不等式(2019年福建省质检)
Dylaaan 发布于 2019-03-30 23:24
例题
已知函数 f ( x ) = x ( e 2 x − a ) f(x) = x(e^{2x} - a) f(x)=x(e2x−a),求解以下问题:
- 若 y = 2 x y = 2x y=2x 是曲线 y = f ( x ) y = f(x) y=f(x) 的切线,求 a a a 的值;
- 若 f ( x ) ≥ 1 + x + ln x f(x) \geq 1 + x + \ln x f(x)≥1+x+lnx,求 a a a 的取值范围。
解答
第(1)问求解
由切线的几何性质(切线斜率等于函数在切点处的导数值,且切点在切线与曲线上),可解得 a = − 1 a = -1 a=−1,具体推导过程此处从略。
第(2)问求解
首先利用常见不等式 e t ≥ t + 1 e^t \geq t + 1 et≥t+1(当且仅当 t = 0 t = 0 t=0 时取等号),令 t = 2 x + ln x t = 2x + \ln x t=2x+lnx,则有:
e 2 x + ln x ≥ ( 2 x + ln x ) + 1 e^{2x + \ln x} \geq (2x + \ln x) + 1 e2x+lnx≥(2x+lnx)+1
由于 e 2 x + ln x = e 2 x ⋅ e ln x = x e 2 x e^{2x + \ln x} = e^{2x} \cdot e^{\ln x} = x e^{2x} e2x+lnx=e2x⋅elnx=xe2x,因此上述不等式可化为:
x e 2 x ≥ 2 x + ln x + 1 x e^{2x} \geq 2x + \ln x + 1 xe2x≥2x+lnx+1(当且仅当 2 x + ln x = 0 2x + \ln x = 0 2x+lnx=0 时取等号)。
原不等式 f ( x ) ≥ 1 + x + ln x f(x) \geq 1 + x + \ln x f(x)≥1+x+lnx 可变形为:
x e 2 x ≥ ( a + 1 ) x + ln x + 1 x e^{2x} \geq (a + 1)x + \ln x + 1 xe2x≥(a+1)x+lnx+1
分情况讨论:
-
当 a ≤ 1 a \leq 1 a≤1 时:
因 x > 0 x > 0 x>0,不等式两边乘正数 x x x 不改变方向,故 ( a + 1 ) x ≤ 2 x (a + 1)x \leq 2x (a+1)x≤2x。结合 x e 2 x ≥ 2 x + ln x + 1 x e^{2x} \geq 2x + \ln x + 1 xe2x≥2x+lnx+1,可得:
x e 2 x ≥ 2 x + ln x + 1 ≥ ( a + 1 ) x + ln x + 1 x e^{2x} \geq 2x + \ln x + 1 \geq (a + 1)x + \ln x + 1 xe2x≥2x+lnx+1≥(a+1)x+lnx+1
此时原不等式恒成立,满足条件。
-
当 a > 1 a > 1 a>1 时:
取 x 0 > 0 x_0 > 0 x0>0 满足 2 x 0 + ln x 0 = 0 2x_0 + \ln x_0 = 0 2x0+lnx0=0,对该式两边同取指数 e e e,得
e 2 x 0 + ln x 0 = e 0 = 1 e^{2x_0 + \ln x_0} = e^0 = 1 e2x0+lnx0=e0=1,
即
e 2 x 0 ⋅ e ln x 0 = x 0 e 2 x 0 = 1 e^{2x_0} \cdot e^{\ln x_0} = x_0 e^{2x_0} = 1 e2x0⋅elnx0=x0e2x0=1
将 x = x 0 x = x_0 x=x0 代入原不等式 x e 2 x ≥ ( a + 1 ) x + ln x + 1 x e^{2x} \geq (a + 1)x + \ln x + 1 xe2x≥(a+1)x+lnx+1,
结合 x 0 e 2 x 0 = 1 x_0 e^{2x_0} = 1 x0e2x0=1 与 2 x 0 + ln x 0 = 0 2x_0 + \ln x_0 = 0 2x0+lnx0=0(即 ln x 0 = − 2 x 0 \ln x_0 = -2x_0 lnx0=−2x0),化简得:
1 ≥ ( a + 1 ) x 0 − 2 x 0 + 1 1 \geq (a + 1)x_0 - 2x_0 + 1 1≥(a+1)x0−2x0+1
进一步整理为 ( a − 1 ) x 0 ≤ 0 (a - 1)x_0 \leq 0 (a−1)x0≤0。
由于 a > 1 a > 1 a>1 且 x 0 > 0 x_0 > 0 x0>0,显然 ( a − 1 ) x 0 > 0 (a - 1)x_0 > 0 (a−1)x0>0,与上式矛盾,故 a > 1 a > 1 a>1 不满足条件。
综上, a a a 的取值范围是 ( − ∞ , 1 ] (-\infty, 1] (−∞,1]。
注释
上述第(2)问中所取的 x 0 x_0 x0 可表示为 1 2 W ( 2 ) \frac{1}{2}W(2) 21W(2),其中 W ( ⋅ ) W(\cdot) W(⋅) 为朗博函数(Lambert W 函数)。
变式题
已知函数 f ( x ) = ln x + 1 − x a x f(x) = \ln x + \frac{1 - x}{ax} f(x)=lnx+ax1−x( a ∈ R a \in \mathbb{R} a∈R 且 a ≠ 0 a \neq 0 a=0), g ( x ) = ( b − 1 ) x − x e x − 1 x g(x) = (b - 1)x - x e^x - \frac{1}{x} g(x)=(b−1)x−xex−x1( b ∈ R b \in \mathbb{R} b∈R),求解以下问题:
- 讨论函数 f ( x ) f(x) f(x) 的单调性;
- 当 a = 1 a = 1 a=1 时,若关于 x x x 的不等式 f ( x ) + g ( x ) ≤ − 2 f(x) + g(x) \leq -2 f(x)+g(x)≤−2 恒成立,求实数 b b b 的取值范围。
【导数压轴题】Lambert W 函数与隐零点
Dylaaan 发布于 2019-03-31 19:51・北京
Lambert W 函数也称朗博函数,该函数可作为近期福建省质检导数压轴题的背景。
此前]并未打算单独撰写该内容,认为无需特意介绍这类较为复杂的知识;但鉴于该函数已多次出现,了解其相关内容仍有一定益处。
一、“隐零点” 的处理策略
取例于 【导数压轴题】“隐零点”的处理策略 - 知乎
https://zhuanlan.zhihu.com/p/57071380
例 1
当 x > 0 x > 0 x>0 时,证明: x e x ≥ x + ln x + 1 x e^{x} \geq x + \ln x + 1 xex≥x+lnx+1。
证明 1
令 f ( x ) = x e x − x − ln x − 1 f (x) = x e^{x} - x - \ln x - 1 f(x)=xex−x−lnx−1,求导得:
f ′ ( x ) = ( x + 1 ) ( e x − 1 x ) f'(x) = (x + 1)\left (e^{x} - \frac {1}{x}\right) f′(x)=(x+1)(ex−x1)
注意到 x + 1 > 0 x + 1 > 0 x+1>0(因 x > 0 x > 0 x>0),令 g ( x ) = e x − 1 x g (x) = e^{x} - \frac {1}{x} g(x)=ex−x1,显然 g ( x ) g (x) g(x) 在 x > 0 x > 0 x>0 时单调递增(因 e x e^{x} ex 单调递增, − 1 x -\frac {1}{x} −x1 单调递增,增函数加增函数仍为增函数)。
代入特殊值计算:
g ( 1 2 ) = e − 2 < 0 g\left (\frac {1}{2}\right) = \sqrt {e} - 2 < 0 g(21)=e−2<0, g ( 1 ) = e − 1 > 0 g (1) = e - 1 > 0 g(1)=e−1>0
根据零点存在定理,存在 x 0 ∈ ( 1 2 , 1 ) x_{0} \in \left (\frac {1}{2}, 1\right) x0∈(21,1),使得 g ( x 0 ) = 0 g (x_{0}) = 0 g(x0)=0,等价变形为:
e x 0 = 1 x 0 ⇔ ln x 0 = − x 0 e^{x_{0}} = \frac {1}{x_{0}} \Leftrightarrow \ln x_{0} = -x_{0} ex0=x01⇔lnx0=−x0
由此可知 f ( x ) f (x) f(x) 的单调性:在 ( 0 , x 0 ) (0, x_{0}) (0,x0) 上单调递减(因 g ( x ) < 0 g (x) < 0 g(x)<0,故 f ′ ( x ) < 0 f'(x) < 0 f′(x)<0),在 ( x 0 , + ∞ ) (x_{0}, +\infty) (x0,+∞) 上单调递增(因 g ( x ) > 0 g (x) > 0 g(x)>0,故 f ′ ( x ) > 0 f'(x) > 0 f′(x)>0)。
因此 f ( x ) f (x) f(x) 的最小值为 f ( x 0 ) f (x_{0}) f(x0),代入 e x 0 = 1 x 0 e^{x_{0}} = \frac {1}{x_{0}} ex0=x01 和 ln x 0 = − x 0 \ln x_{0} = -x_{0} lnx0=−x0 计算:
f ( x 0 ) = x 0 e x 0 − x 0 − ln x 0 − 1 = x 0 ⋅ 1 x 0 − x 0 − ( − x 0 ) − 1 = 1 − x 0 + x 0 − 1 = 0 f (x_{0}) = x_{0} e^{x_{0}} - x_{0} - \ln x_{0} - 1 \\= x_{0} \cdot \frac {1}{x_{0}} - x_{0} - (-x_{0}) - 1 \\= 1 - x_{0} + x_{0} - 1 \\= 0 f(x0)=x0ex0−x0−lnx0−1=x0⋅x01−x0−(−x0)−1=1−x0+x0−1=0
故 f ( x ) ≥ f ( x 0 ) = 0 f (x) \geq f (x_{0}) = 0 f(x)≥f(x0)=0,即 x e x ≥ x + ln x + 1 x e^{x} \geq x + \ln x + 1 xex≥x+lnx+1,证毕。
证明 2
利用常见放缩式 e t ≥ t + 1 e^{t} \geq t + 1 et≥t+1(取等条件为 t = 0 t = 0 t=0),令 t = x + ln x t = x + \ln x t=x+lnx,代入得:
e x + ln x ≥ ( x + ln x ) + 1 e^{x + \ln x} \geq (x + \ln x) + 1 ex+lnx≥(x+lnx)+1
左侧化简: e x + ln x = e x ⋅ e ln x = x e x e^{x + \ln x} = e^{x} \cdot e^{\ln x} = x e^{x} ex+lnx=ex⋅elnx=xex,因此有:
x e x ≥ x + ln x + 1 x e^{x} \geq x + \ln x + 1 xex≥x+lnx+1
取等条件为 t = 0 t = 0 t=0,即 x + ln x = 0 x + \ln x = 0 x+lnx=0,进一步等价于 x e x = 1 x e^{x} = 1 xex=1(两边同乘 e x e^{x} ex 得 x e x = e 0 = 1 x e^{x} = e^{0} = 1 xex=e0=1),此时 x = x 0 x = x_{0} x=x0(即例 1 中 “隐零点”)。
此处应用了方程 x e x = 1 x e^{x} = 1 xex=1 的解,虽无法求出该解的精确值,但可通过代数变形利用该方程,这便是 “隐零点” 的思想。
二、Lambert W 函数
考虑函数 f ( x ) = x e x f (x) = x e^{x} f(x)=xex( x ∈ R x \in \mathbb {R} x∈R),求导得 f ′ ( x ) = ( x + 1 ) e x f'(x) = (x + 1) e^{x} f′(x)=(x+1)ex,据此分析单调性:
- 当 x < − 1 x < -1 x<−1 时, x + 1 < 0 x + 1 < 0 x+1<0 且 e x > 0 e^{x} > 0 ex>0,故 f ′ ( x ) < 0 f'(x) < 0 f′(x)<0, f ( x ) f (x) f(x) 单调递减;
- 当 x > − 1 x > -1 x>−1 时, x + 1 > 0 x + 1 > 0 x+1>0 且 e x > 0 e^{x} > 0 ex>0,故 f ′ ( x ) > 0 f'(x) > 0 f′(x)>0, f ( x ) f (x) f(x) 单调递增。

方程 x 0 e x 0 = 1 x_{0} e^{x_{0}} = 1 x0ex0=1 等价于 f ( x 0 ) = 1 f (x_{0}) = 1 f(x0)=1,进一步等价于 x 0 = f − 1 ( 1 ) x_{0} = f^{-1}(1) x0=f−1(1)(其中 f − 1 ( x ) f^{-1}(x) f−1(x) 为 y = f ( x ) y = f (x) y=f(x) 的反函数)。
为简化表示,定义 Lambert W 函数:
- 当 x ≥ − 1 x \geq -1 x≥−1 时,记 W ( x ) = f − 1 ( x ) W (x) = f^{-1}(x) W(x)=f−1(x)(对应 f ( x ) f (x) f(x) 在 x ≥ − 1 x \geq -1 x≥−1 上的反函数);
- 当 x ≤ − 1 x \leq -1 x≤−1 时,记 W − 1 ( x ) = f − 1 ( x ) W_{-1}(x) = f^{-1}(x) W−1(x)=f−1(x)(对应 f ( x ) f (x) f(x) 在 x ≤ − 1 x \leq -1 x≤−1 上的反函数)。
(注:此定义为简化理解的方式,非 Lambert W 函数的原始定义。)
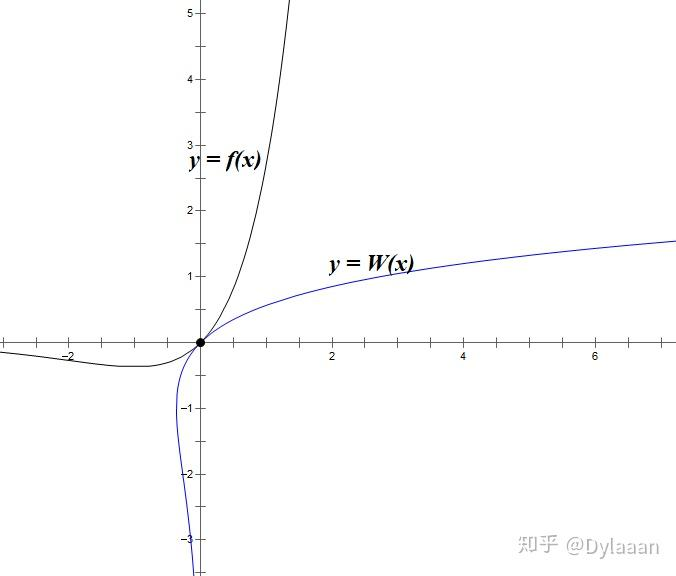
基于上述定义,方程 x 0 e x 0 = 1 x_{0} e^{x_{0}} = 1 x0ex0=1 的根可表示为 x 0 = W ( 1 ) x_{0} = W (1) x0=W(1),且该方程等价于 x 0 + ln x 0 = 0 x_{0} + \ln x_{0} = 0 x0+lnx0=0(关键变形,需牢记)。
延伸示例:方程
2
x
0
+
ln
x
0
=
0
2 x_{0} + \ln x_{0} = 0
2x0+lnx0=0 的根如何用 Lambert W 函数表示?
对等式进行等价变形:
2
x
0
+
ln
x
0
=
0
⇔
ln
x
0
=
−
2
x
0
⇔
x
0
=
e
−
2
x
0
⇔
x
0
e
2
x
0
=
1
2 x_{0} + \ln x_{0} = 0 \Leftrightarrow \ln x_{0} = -2 x_{0} \Leftrightarrow x_{0} = e^{-2 x_{0}} \Leftrightarrow x_{0} e^{2 x_{0}} = 1
2x0+lnx0=0⇔lnx0=−2x0⇔x0=e−2x0⇔x0e2x0=1
两边同乘 2 得: 2 x 0 e 2 x 0 = 2 2 x_{0} e^{2 x_{0}} = 2 2x0e2x0=2,令 t = 2 x 0 t = 2 x_{0} t=2x0,则 t e t = 2 t e^{t} = 2 tet=2,根据 Lambert W 函数定义, t = W ( 2 ) t = W (2) t=W(2),因此 x 0 = 1 2 W ( 2 ) x_{0} = \frac {1}{2} W (2) x0=21W(2)。
该方程曾出现在近年福建省质检的导数压轴题中。
三、用 Lambert W 函数解决一类导数 “难题”
例 2
若不等式 x e x ≥ a x + ln x + 1 x e^{x} \geq a x + \ln x + 1 xex≥ax+lnx+1 对 x > 0 x > 0 x>0 恒成立,求实数 a a a 的取值范围。
分析
由例 1 已证 x e x ≥ x + ln x + 1 x e^{x} \geq x + \ln x + 1 xex≥x+lnx+1,因此:
- 当 a ≤ 1 a \leq 1 a≤1 时, a x + ln x + 1 ≤ x + ln x + 1 ≤ x e x a x + \ln x + 1 \leq x + \ln x + 1 \leq x e^{x} ax+lnx+1≤x+lnx+1≤xex,原不等式恒成立;
- 需进一步验证 a > 1 a > 1 a>1 时原不等式是否恒成立:若能找到某个 x 0 > 0 x_{0} > 0 x0>0 使不等式不成立,即可排除 a > 1 a > 1 a>1。
结合例 1 中 “隐零点” 的取等条件:不等式 x e x ≥ x + ln x + 1 x e^{x} \geq x + \ln x + 1 xex≥x+lnx+1 的取等点为 x 0 = W ( 1 ) x_{0} = W (1) x0=W(1)(即 x 0 e x 0 = 1 x_{0} e^{x_{0}} = 1 x0ex0=1 且 x 0 + ln x 0 = 0 x_{0} + \ln x_{0} = 0 x0+lnx0=0)。
将
x
=
x
0
x = x_{0}
x=x0 代入原不等式:
x
0
e
x
0
≥
a
x
0
+
ln
x
0
+
1
x_{0} e^{x_{0}} \geq a x_{0} + \ln x_{0} + 1
x0ex0≥ax0+lnx0+1
代入
x
0
e
x
0
=
1
x_{0} e^{x_{0}} = 1
x0ex0=1 和
x
0
+
ln
x
0
=
0
x_{0} + \ln x_{0} = 0
x0+lnx0=0(即
ln
x
0
=
−
x
0
\ln x_{0} = -x_{0}
lnx0=−x0),化简得:
1
≥
a
x
0
−
x
0
+
1
⇔
0
≥
(
a
−
1
)
x
0
1 \geq a x_{0} - x_{0} + 1 \Leftrightarrow 0 \geq (a - 1) x_{0}
1≥ax0−x0+1⇔0≥(a−1)x0
因 x 0 > 0 x_{0} > 0 x0>0,故 ( a − 1 ) ≤ 0 ⇔ a ≤ 1 (a - 1) \leq 0 \Leftrightarrow a \leq 1 (a−1)≤0⇔a≤1,与 a > 1 a > 1 a>1 矛盾,因此 a > 1 a > 1 a>1 时原不等式不恒成立。
结论
实数 a a a 的取值范围为 a ≤ 1 a \leq 1 a≤1。
注:此题等价于 2019 年龙岩市 3 月质检导数压轴题
- 【028】指对不等式(2019年龙岩3月质检) - 知乎
https://zhuanlan.zhihu.com/p/58086379
例 3
若不等式 x e 2 x ≥ a x + ln x + 1 x e^{2 x} \geq a x + \ln x + 1 xe2x≥ax+lnx+1 对 x > 0 x > 0 x>0 恒成立,求实数 a a a 的取值范围。
分析
利用常见放缩式
e
t
≥
t
+
1
e^{t} \geq t + 1
et≥t+1(取等条件
t
=
0
t = 0
t=0),令
t
=
2
x
+
ln
x
t = 2 x + \ln x
t=2x+lnx,代入得:
e
2
x
+
ln
x
≥
(
2
x
+
ln
x
)
+
1
e^{2 x + \ln x} \geq (2 x + \ln x) + 1
e2x+lnx≥(2x+lnx)+1
左侧化简:
e
2
x
+
ln
x
=
e
2
x
⋅
e
ln
x
=
x
e
2
x
e^{2 x + \ln x} = e^{2 x} \cdot e^{\ln x} = x e^{2 x}
e2x+lnx=e2x⋅elnx=xe2x,因此有:
x
e
2
x
≥
2
x
+
ln
x
+
1
x e^{2 x} \geq 2 x + \ln x + 1
xe2x≥2x+lnx+1
后续分析同例 2:
- 当 a ≤ 2 a \leq 2 a≤2 时, a x + ln x + 1 ≤ 2 x + ln x + 1 ≤ x e 2 x a x + \ln x + 1 \leq 2 x + \ln x + 1 \leq x e^{2 x} ax+lnx+1≤2x+lnx+1≤xe2x,原不等式恒成立;
- 当 a > 2 a > 2 a>2 时,取取等点 x 0 x_{0} x0(满足 2 x 0 + ln x 0 = 0 2 x_{0} + \ln x_{0} = 0 2x0+lnx0=0,即 x 0 = 1 2 W ( 2 ) x_{0} = \frac {1}{2} W (2) x0=21W(2)),代入原不等式可推出矛盾,故 a > 2 a > 2 a>2 不成立。
结论
实数 a a a 的取值范围为 a ≤ 2 a \leq 2 a≤2。
注:此题等价于 2019 年福建省质检导数压轴题
-【040】朗博函数与不等式(2019年福建省质检) - 知乎
https://zhuanlan.zhihu.com/p/60928836
这类题目初次接触时会觉得 “新颖”,但后续频繁出现在各类模拟考试中。
个人认为,此类题目偏向特殊技巧,且可通过固定方法快速解决,不适合作为考试题;但鉴于其高频出现,仍需整理相关思路。
【高中数学・导数】朗博 W 函数与常规方法
Dreaming 发布于2021-04-23 00:49
一、题目
已知不等式 x ( e 2 x − a ) ≥ 1 + x + ln x x (e^{2 x} - a) \geq 1 + x + \ln x x(e2x−a)≥1+x+lnx 对 x > 0 x > 0 x>0 恒成立,求实数 a a a 的取值范围。
二、解答
方法一(分参 + Lambert W 函数)
步骤 1:分离参数
对原不等式变形,分离出参数
a
a
a:
x
e
2
x
−
a
x
≥
1
+
x
+
ln
x
⇔
a
x
≤
x
e
2
x
−
1
−
x
−
ln
x
x e^{2 x} - a x \geq 1 + x + \ln x \Leftrightarrow a x \leq x e^{2 x} - 1 - x - \ln x
xe2x−ax≥1+x+lnx⇔ax≤xe2x−1−x−lnx
因
x
>
0
x > 0
x>0,两边同除以
x
x
x 得:
a
≤
e
2
x
−
1
+
x
+
ln
x
x
a \leq e^{2 x} - \frac {1 + x + \ln x}{x}
a≤e2x−x1+x+lnx
令 f ( x ) = e 2 x − 1 + x + ln x x f (x) = e^{2 x} - \frac {1 + x + \ln x}{x} f(x)=e2x−x1+x+lnx,问题转化为求 f ( x ) f (x) f(x) 的最小值 f min f_{\text {min}} fmin,则 a ≤ f min a \leq f_{\text {min}} a≤fmin。
步骤 2:分析 f ( x ) f (x) f(x) 的单调性(找 “隐零点”)
对
f
(
x
)
f (x)
f(x) 求导:
f
′
(
x
)
=
2
e
2
x
−
(
1
+
1
x
)
⋅
x
−
(
1
+
x
+
ln
x
)
⋅
1
x
2
f'(x) = 2 e^{2 x} - \frac {(1 + \frac {1}{x}) \cdot x - (1 + x + \ln x) \cdot 1}{x^{2}}
f′(x)=2e2x−x2(1+x1)⋅x−(1+x+lnx)⋅1
化简导数分母与分子:
- 分母: x 2 x^{2} x2( x > 0 x > 0 x>0,故分母恒正);
- 分子: ( x + 1 ) − ( 1 + x + ln x ) = − ln x (x + 1) - (1 + x + \ln x) = -\ln x (x+1)−(1+x+lnx)=−lnx;
因此 f ′ ( x ) = 2 e 2 x + ln x x 2 f'(x) = 2 e^{2 x} + \frac {\ln x}{x^{2}} f′(x)=2e2x+x2lnx(注意符号:负负得正)。
分析 f ′ ( x ) f'(x) f′(x) 的零点:
- 当 x = e − 2 x = e^{-2} x=e−2 时, f ′ ( e − 2 ) = 2 e 2 ⋅ e − 2 + ln e − 2 ( e − 2 ) 2 = 2 e 2 e − 2 − 2 e − 4 = 2 e 2 e − 2 − 2 e 4 < 0 f'(e^{-2}) = 2 e^{2 \cdot e^{-2}} + \frac {\ln e^{-2}}{(e^{-2})^{2}} = 2 e^{2 e^{-2}} - \frac {2}{e^{-4}} = 2 e^{2 e^{-2}} - 2 e^{4} < 0 f′(e−2)=2e2⋅e−2+(e−2)2lne−2=2e2e−2−e−42=2e2e−2−2e4<0;
- 当 x = 1 x = 1 x=1 时, f ′ ( 1 ) = 2 e 2 ⋅ 1 + ln 1 1 2 = 2 e 2 + 0 > 0 f'(1) = 2 e^{2 \cdot 1} + \frac {\ln 1}{1^{2}} = 2 e^{2} + 0 > 0 f′(1)=2e2⋅1+12ln1=2e2+0>0;
因
f
′
(
x
)
f'(x)
f′(x) 在
x
>
0
x > 0
x>0 上连续(
e
2
x
e^{2 x}
e2x、
ln
x
\ln x
lnx 均连续),根据零点存在定理,存在
x
0
∈
(
e
−
2
,
1
)
x_{0} \in (e^{-2}, 1)
x0∈(e−2,1),使得
f
′
(
x
0
)
=
0
f'(x_{0}) = 0
f′(x0)=0,即:
2
e
2
x
0
+
ln
x
0
x
0
2
=
0
2 e^{2 x_{0}} + \frac {\ln x_{0}}{x_{0}^{2}} = 0
2e2x0+x02lnx0=0
步骤 3:用 Lambert W 函数化简 “隐零点”
对
f
′
(
x
0
)
=
0
f'(x_{0}) = 0
f′(x0)=0 进行等价变形:
2
e
2
x
0
=
−
ln
x
0
x
0
2
⇔
2
x
0
2
e
2
x
0
=
−
ln
x
0
⇔
2
x
0
e
2
x
0
=
−
ln
x
0
x
0
2 e^{2 x_{0}} = -\frac {\ln x_{0}}{x_{0}^{2}} \Leftrightarrow 2 x_{0}^{2} e^{2 x_{0}} = -\ln x_{0} \Leftrightarrow 2 x_{0} e^{2 x_{0}} = -\frac {\ln x_{0}}{x_{0}}
2e2x0=−x02lnx0⇔2x02e2x0=−lnx0⇔2x0e2x0=−x0lnx0
右侧进一步变形: − ln x 0 x 0 = − ln x 0 ⋅ e − ln x 0 -\frac {\ln x_{0}}{x_{0}} = -\ln x_{0} \cdot e^{-\ln x_{0}} −x0lnx0=−lnx0⋅e−lnx0(因 e − ln x 0 = 1 x 0 e^{-\ln x_{0}} = \frac {1}{x_{0}} e−lnx0=x01)。
令
g
(
t
)
=
t
e
t
g (t) = t e^{t}
g(t)=tet,则上述等式可表示为:
g
(
2
x
0
)
=
g
(
−
ln
x
0
)
g (2 x_{0}) = g (-\ln x_{0})
g(2x0)=g(−lnx0)
分析 g ( t ) g (t) g(t) 的单调性: g ′ ( t ) = ( t + 1 ) e t g'(t) = (t + 1) e^{t} g′(t)=(t+1)et,当 t > 0 t > 0 t>0 时, t + 1 > 0 t + 1 > 0 t+1>0 且 e t > 0 e^{t} > 0 et>0,故 g ( t ) g (t) g(t) 在 ( 0 , + ∞ ) (0, +\infty) (0,+∞) 上单调递增。
因 x 0 ∈ ( e − 2 , 1 ) x_{0} \in (e^{-2}, 1) x0∈(e−2,1),故 2 x 0 > 0 2 x_{0} > 0 2x0>0, − ln x 0 > 0 -\ln x_{0} > 0 −lnx0>0( ln x 0 < 0 \ln x_{0} < 0 lnx0<0),即 2 x 0 2 x_{0} 2x0 和 − ln x 0 -\ln x_{0} −lnx0 均在 g ( t ) g (t) g(t) 的单调递增区间内。
由单调性可知: 2 x 0 = − ln x 0 2 x_{0} = -\ln x_{0} 2x0=−lnx0(单调函数若 g ( a ) = g ( b ) g (a) = g (b) g(a)=g(b),则 a = b a = b a=b)。
步骤 4:计算 f ( x ) f (x) f(x) 的最小值 f ( x 0 ) f (x_{0}) f(x0)
将
2
x
0
=
−
ln
x
0
2 x_{0} = -\ln x_{0}
2x0=−lnx0(即
ln
x
0
=
−
2
x
0
\ln x_{0} = -2 x_{0}
lnx0=−2x0)代入
f
(
x
0
)
f (x_{0})
f(x0):
f
(
x
0
)
=
e
2
x
0
−
1
+
x
0
+
ln
x
0
x
0
=
e
2
x
0
−
1
+
x
0
−
2
x
0
x
0
=
e
2
x
0
−
1
−
x
0
x
0
f (x_{0}) = e^{2 x_{0}} - \frac {1 + x_{0} + \ln x_{0}}{x_{0}} = e^{2 x_{0}} - \frac {1 + x_{0} - 2 x_{0}}{x_{0}} = e^{2 x_{0}} - \frac {1 - x_{0}}{x_{0}}
f(x0)=e2x0−x01+x0+lnx0=e2x0−x01+x0−2x0=e2x0−x01−x0
再结合
2
x
0
=
−
ln
x
0
2 x_{0} = -\ln x_{0}
2x0=−lnx0 的变形
e
2
x
0
=
e
−
ln
x
0
=
1
x
0
e^{2 x_{0}} = e^{-\ln x_{0}} = \frac {1}{x_{0}}
e2x0=e−lnx0=x01,代入得:
f
(
x
0
)
=
1
x
0
−
1
−
x
0
x
0
=
1
−
(
1
−
x
0
)
x
0
=
x
0
x
0
=
1
f (x_{0}) = \frac {1}{x_{0}} - \frac {1 - x_{0}}{x_{0}} = \frac {1 - (1 - x_{0})}{x_{0}} = \frac {x_{0}}{x_{0}} = 1
f(x0)=x01−x01−x0=x01−(1−x0)=x0x0=1
因此 f min = 1 f_{\text {min}} = 1 fmin=1,故 a ≤ 1 a \leq 1 a≤1。
说明
此处 Lambert W 函数的核心应用是:对形如 x e x + ln x x = 0 x e^{x} + \frac {\ln x}{x} = 0 xex+xlnx=0 的式子,通过变形 x e x = − ln x x = − ln x ⋅ e − ln x x e^{x} = -\frac {\ln x}{x} = -\ln x \cdot e^{-\ln x} xex=−xlnx=−lnx⋅e−lnx,结合 g ( t ) = t e t g (t) = t e^{t} g(t)=tet 的单调性,得到 x = − ln x x = -\ln x x=−lnx,从而消去 “隐零点” 中的未知项。
方法二(经典放缩法)
步骤 1:利用常见指对放缩式
常见放缩式: t e t = e t + ln t ≥ 1 + t + ln t t e^{t} = e^{t + \ln t} \geq 1 + t + \ln t tet=et+lnt≥1+t+lnt(取等条件为 t + ln t = 0 t + \ln t = 0 t+lnt=0,即 t e t = 1 t e^{t} = 1 tet=1)。
对原不等式进行整理,构造与放缩式匹配的结构:
原不等式
x
(
e
2
x
−
a
)
≥
1
+
x
+
ln
x
x (e^{2 x} - a) \geq 1 + x + \ln x
x(e2x−a)≥1+x+lnx 变形为:
x
e
2
x
≥
1
+
(
a
+
1
)
x
+
ln
x
x e^{2 x} \geq 1 + (a + 1) x + \ln x
xe2x≥1+(a+1)x+lnx
左侧进一步化简:
x
e
2
x
=
e
2
x
+
ln
x
x e^{2 x} = e^{2 x + \ln x}
xe2x=e2x+lnx(同方法一),因此原不等式等价于:
e
2
x
+
ln
x
≥
1
+
(
a
+
1
)
x
+
ln
x
e^{2 x + \ln x} \geq 1 + (a + 1) x + \ln x
e2x+lnx≥1+(a+1)x+lnx
步骤 2:分情况讨论 a a a 的取值
-
当 a ≤ 1 a \leq 1 a≤1 时:
因 a ≤ 1 a \leq 1 a≤1,故 ( a + 1 ) x ≤ 2 x (a + 1) x \leq 2 x (a+1)x≤2x,因此:
1 + ( a + 1 ) x + ln x ≤ 1 + 2 x + ln x 1 + (a + 1) x + \ln x \leq 1 + 2 x + \ln x 1+(a+1)x+lnx≤1+2x+lnx结合放缩式 e 2 x + ln x ≥ 1 + 2 x + ln x e^{2 x + \ln x} \geq 1 + 2 x + \ln x e2x+lnx≥1+2x+lnx,可得:
e 2 x + ln x ≥ 1 + ( a + 1 ) x + ln x e^{2 x + \ln x} \geq 1 + (a + 1) x + \ln x e2x+lnx≥1+(a+1)x+lnx,原不等式恒成立。 -
当 a > 1 a > 1 a>1 时:
放缩式 e 2 x + ln x = 1 + 2 x + ln x e^{2 x + \ln x} = 1 + 2 x + \ln x e2x+lnx=1+2x+lnx 的取等条件为 2 x + ln x = 0 2 x + \ln x = 0 2x+lnx=0,易知该方程有解(设解为 x 0 x_{0} x0)。将 x = x 0 x = x_{0} x=x0 代入原不等式右侧:
1 + ( a + 1 ) x 0 + ln x 0 = 1 + ( a + 1 ) x 0 − 2 x 0 = 1 + ( a − 1 ) x 0 1 + (a + 1) x_{0} + \ln x_{0} = 1 + (a + 1) x_{0} - 2 x_{0} = 1 + (a - 1) x_{0} 1+(a+1)x0+lnx0=1+(a+1)x0−2x0=1+(a−1)x0因 a > 1 a > 1 a>1 且 x 0 > 0 x_{0} > 0 x0>0,故 1 + ( a − 1 ) x 0 > 1 + 2 x 0 + ln x 0 = e 2 x 0 + ln x 0 1 + (a - 1) x_{0} > 1 + 2 x_{0} + \ln x_{0} = e^{2 x_{0} + \ln x_{0}} 1+(a−1)x0>1+2x0+lnx0=e2x0+lnx0,与原不等式矛盾。
结论
实数 a a a 的取值范围为 a ≤ 1 a \leq 1 a≤1。
- Lambert W 函数 | 导数应用(隐零点、常规方法)与函数性质(篇 1)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/154015504
via:
-
【导数压轴题】Lambert W 函数与隐零点 - 知乎 2019
https://zhuanlan.zhihu.com/p/60979387 -
【040】朗博函数与不等式(2019年福建省质检) - 知乎
https://zhuanlan.zhihu.com/p/60928836 -
【高中数学·导数】朗博 W 函数与常规方法 - 知乎 2021
https://zhuanlan.zhihu.com/p/367080386- 浅谈误差函数 erf(x) - 知乎 2020
https://zhuanlan.zhihu.com/p/164894362 - 朗伯函数在高考数字中的应用_朗伯函数的高中应用-优快云博客
https://blog.youkuaiyun.com/wwxy1995/article/details/105466758
- 浅谈误差函数 erf(x) - 知乎 2020





















 2180
2180

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








