线性代数 | 秩—零化度定理

注：本文为 “线性代数 · 秩—零化度定理” 相关合辑。
英文引文，机翻未校。
中文引文，略作重排。
如有内容异常，请看原文。

---

Rank and Nullity

秩与零化度

Rank and Nullity are two essential concepts related to matrices in Linear Algebra. The nullity of a matrix is determined by the difference between the order and rank of the matrix. The rank of a matrix is the number of linearly independent row or column vectors of a matrix. If $n$ is the order of the square matrix $A$, then the nullity of $A$ is given by $n–r$. Thus, the rank of a matrix is the number of linearly independent or non-zero vectors of a matrix, whereas nullity is the number of zero vectors of a matrix.
在线性代数中，秩（Rank）与零化度（Nullity）是与矩阵相关的两个核心概念。矩阵的零化度由其阶数与秩的差值确定，矩阵的秩则是矩阵中线性无关的行向量或列向量的数量。若 $n$ 为方阵 $A$ 的阶数，则 $A$ 的零化度可表示为 $n–r$（其中 $r$ 为矩阵的秩）。因此，矩阵的秩是矩阵中线性无关向量（或非零向量）的数量，而零化度是矩阵中零向量的数量。

The rank of matrix $A$ is denoted as $\rho (A)$, and the nullity is denoted as $N(A)$. Evidently, if the rank of the matrix is equal to the order of the matrix, then the nullity of the matrix is zero.
矩阵 $A$ 的秩记为 $\rho (A)$，零化度记为 $N(A)$。显然，若矩阵的秩等于其阶数，则该矩阵的零化度为 0。

Rank and Nullity Theorem for Matrix

矩阵的秩-零化度定理

The rank and nullity theorem for matrices is one of the important theorems in linear algebra and a requirement to derive many more results. Before discussing the theorem, we must know the concept of null spaces.
矩阵的秩-零化度定理是线性代数中的重要定理之一，也是推导更多结论的基础。在讨论该定理之前，我们需要先了解零空间（Null Space）的概念。

Nullspace

零空间

Let $A$ be a real matrix of order $m\times n$, the set of the solutions associated with the system of homogeneous equation $\mathbf{AX}=0$ is said to be the null space of $A$.
设 $A$ 为 $m\times n$ 阶实矩阵，齐次方程组 $\mathbf{AX}=0$ 的所有解构成的集合，称为矩阵 $A$ 的零空间。

Nullspace of $A$ = { x ∈ R n ∣ A x = 0 } \{ x \in \boldsymbol{R}^n \mid Ax = 0 \} {x∈Rn∣Ax=0}. Then the nullity of $A$ will be the dimension of the Nullspace of $A$.
$A$ 的零空间可表示为 { x ∈ R n ∣ A x = 0 } \{ x \in \boldsymbol{R}^n \mid Ax = 0 \} {x∈Rn∣Ax=0}，而 $A$ 的零化度就是其零空间的维数。

If the rank of $A$ is $r$, there are $r$ leading variables in row-reduced echelon form of $A$ and $n–r$ free variables, which are solutions of the homogeneous system of equation $AX=0$. Thus, $n–r$ is the dimension of the null space of $A$. This fact motivates the rank and nullity theorem for matrices.
若 $A$ 的秩为 $r$，则其行简化阶梯形矩阵中含有 $r$ 个主变量（leading variable）和 $n–r$ 个自由变量（free variable），这些自由变量对应齐次方程组 $AX=0$ 的解。因此，$A$ 的零空间维数为 $n–r$，这一结论为矩阵秩-零化度定理的提出提供了依据。

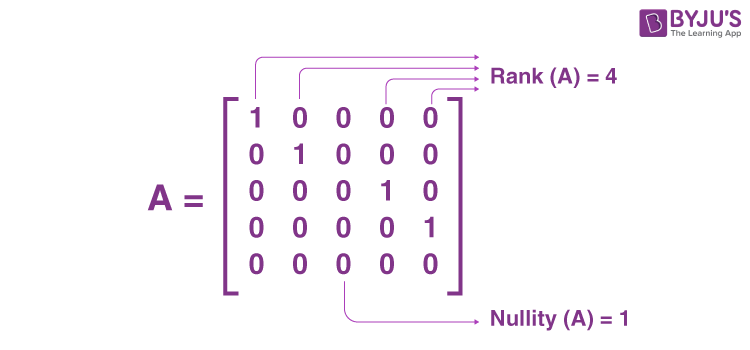
Row-reduced Echelon Form of $A$
矩阵 $A$ 的行简化阶梯形

Rank and Nullity Theorem

秩-零化度定理

If $A$ is a matrix of order $m\times n$, then Rank of $A$ + Nullity of $A$ = Number of columns in $A$ = $n$
若 $A$ 为 $m\times n$ 阶矩阵，则 $A$ 的秩 + $A$ 的零化度 = $A$ 的列数 = $n$

Proof: We already have a result, “Let $A$ be a matrix of order $m\times n$, then the rank of $A$ is equal to the number of leading columns of row-reduced echelon form of $A$.”
证明：已知结论“设 $A$ 为 $m\times n$ 阶矩阵，则 $A$ 的秩等于其行简化阶梯形矩阵中主列（leading column）的数量”。

Let $r$ be the rank of $A$, and then we have two cases as follows:
设 $r$ 为 $A$ 的秩，分以下两种情况讨论：

Case I: If $A$ is a non-singular matrix, then $r=n$ as the row-reduced echelon form will have no zero rows. Then, $x=0$ will be the trivial solution of $AX=0$; that is, the nullity of $A$ will be zero.
情况一： 若 $A$ 为非奇异矩阵（可逆矩阵），则其行简化阶梯形矩阵不含零行，因此 $r=n$。此时，齐次方程组 $AX=0$ 仅有平凡解 $x=0$，即 $A$ 的零化度为 0。

Hence, rank of $A$ + nullity of $A$ = $n+0=n$ = Number of columns in $A$
因此，$A$ 的秩 + $A$ 的零化度 = $n+0=n$ = $A$ 的列数

Case II: If $A$ is singular, then rank of $A$ will be less than the order of $A$, that is, $r<n$. Therefore, there are $r$ non-zero rows or $r$ leading columns of the row-reduced echelon form. Consequently, there will be $n–r$ zero rows, which contributes to the solution of $AX=0$, which means the nullity of $A$ is $n–r$.
情况二： 若 $A$ 为奇异矩阵（不可逆矩阵），则 $A$ 的秩小于其阶数，即 $r<n$。此时，其行简化阶梯形矩阵含有 $r$ 个非零行（或 $r$ 个主列），因此会有 $n–r$ 个零行，这些零行对应齐次方程组 $AX=0$ 的解，即 $A$ 的零化度为 $n–r$。

Hence, rank of $A$ + nullity of $A$ = $r+n–r=n$ = Number of columns in $A$.
因此，$A$ 的秩 + $A$ 的零化度 = $r+(n–r)=n$ = $A$ 的列数。

In both cases, we get the same result which proves our claim.
两种情况均得到相同结论，定理得证。

Important Facts on Rank and Nullity

关于秩与零化度的重要结论

• The rank of an invertible matrix is equal to the order of the matrix, and its nullity is equal to zero.
  可逆矩阵的秩等于其阶数，零化度为 0。

• Rank is the number of leading columns or non-zero row vectors of the row-reduced echelon form of the given matrix, and the number of zero rows is the nullity.
  矩阵的秩等于其行简化阶梯形矩阵中主列或非零行向量的数量，零化度等于其行简化阶梯形矩阵中零行的数量。

• The nullity of a matrix is the dimension of the null space of $A$, also called the kernel of $A$.
  矩阵的零化度是其零空间的维数，零空间也称为核（kernel）。

• If $A$ is an invertible matrix, then null space ($A$) = { 0 } \{0\} {0}.
  若 $A$ 为可逆矩阵，则其零空间 null space ($A$) = { 0 } \{0\} {0}（仅含零向量）。

• The rank of a matrix is the number of non-zero eigenvalues of the matrix, and the number of zero eigenvalues determines the nullity of the matrix.
  矩阵的秩等于其非零特征值的数量，零特征值的数量决定了矩阵的零化度。

Solved Examples on Rank and Nullity

秩与零化度的求解示例

Example 1

示例 1

Verify the rank and nullity theorem for the matrix
验证下述矩阵是否满足秩-零化度定理：

$$A=\left[\begin{array}{cccc}1& 1& 2& 3\\ 3& 4& -1& 2\\ -1& -2& 5& 4\end{array}\right]$$

Solution

解答

Given the matrix:
已知矩阵：

$$A=\left[\begin{array}{cccc}1& 1& 2& 3\\ 3& 4& -1& 2\\ -1& -2& 5& 4\end{array}\right]$$

We reduce $A$ to its row-reduced echelon form through elementary row and column operations:
通过初等行变换与列变换，将 $A$ 化为行简化阶梯形：

1. Apply $R_2\to R_2+(-3)R_1$ and $R_3\to R_3+R_1$
   执行行变换 $R_2\to R_2+(-3)R_1$ 和 $R_3\to R_3+R_1$：
   $$A\sim \left[\begin{array}{cccc}1& 1& 2& 3\\ 0& 1& -7& -7\\ 0& -1& 7& 7\end{array}\right]$$

2. Apply $R_3\to R_3+R_2$
   执行行变换 $R_3\to R_3+R_2$：
   $$A\sim \left[\begin{array}{cccc}1& 1& 2& 3\\ 0& 1& -7& -7\\ 0& 0& 0& 0\end{array}\right]$$

3. Apply $C_2\to C_2+C_1$, $C_3\to C_3+(-2)C_1$ and $C_4\to C_4+(-3)C_1$
   执行列变换 $C_2\to C_2+C_1$、$C_3\to C_3+(-2)C_1$ 和 $C_4\to C_4+(-3)C_1$：
   $$A\sim \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& -7& -7\\ 0& 0& 0& 0\end{array}\right]$$

4. Apply $C_3\to C_3+7C_2$ and $C_4\to C_4+7C_2$
   执行列变换 $C_3\to C_3+7C_2$ 和 $C_4\to C_4+7C_2$：
   $$A\sim \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\end{array}\right]$$

Clearly, $\text{rank}(A)=2$ and $\text{nullity}(A)=2$.
显然，$\text{rank}(A)=2$，$\text{nullity}(A)=2$。

Therefore, $\text{rank}(A)+\text{nullity}(A)=2+2=4$, which equals the number of columns of $A$.
因此，$\text{rank}(A)+\text{nullity}(A)=2+2=4$，等于矩阵 $A$ 的列数。

Example 2

示例 2

Find the nullity of the matrix
求下述矩阵的零化度：

$$A=\left[\begin{array}{cccc}1& 3& 4& 3\\ 3& 9& 12& 9\\ 1& 3& 4& 1\end{array}\right]$$

Solution

解答

Given the matrix:
已知矩阵：

$$A=\left[\begin{array}{cccc}1& 3& 4& 3\\ 3& 9& 12& 9\\ 1& 3& 4& 1\end{array}\right]$$

We reduce $A$ to its row-reduced echelon form through elementary operations:
通过初等变换，将 $A$ 化为行简化阶梯形：

1. Apply elementary row operations $R_{21}(-3)$ (i.e., $R_2=R_2-3R_1$) and $R_{31}(-1)$ (i.e., $R_3=R_3-R_1$)
   执行初等行变换 $R_{21}(-3)$（即 $R_2=R_2-3R_1$）和 $R_{31}(-1)$（即 $R_3=R_3-R_1$）：
   $$A\sim \left[\begin{array}{cccc}1& 3& 4& 3\\ 0& 0& 0& 0\\ 0& 0& 0& -2\end{array}\right]$$

2. Apply elementary row operation $R_3(-\frac{1}{2})$ (i.e., $R_3=-\frac{1}{2}{R}_3$)
   执行初等行变换 $R_3(-\frac{1}{2})$（即 $R_3=-\frac{1}{2}{R}_3$）：
   $$A\sim \left[\begin{array}{cccc}1& 3& 4& 3\\ 0& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

3. Apply elementary column operation $C_{24}$ (i.e., swap Column 2 and Column 4)
   执行初等列变换 $C_{24}$（即交换第 2 列与第 4 列）：
   $$A\sim \left[\begin{array}{cccc}1& 3& 4& 3\\ 0& 1& 0& 0\\ 0& 0& 0& 0\end{array}\right]$$

4. Apply elementary column operations $C_{21}(-3)$ (i.e., $C_2=C_2-3C_1$), $C_{31}(-4)$ (i.e., $C_3=C_3-4C_1$) and $C_{41}(-3)$ (i.e., $C_4=C_4-3C_1$)
   执行初等列变换 $C_{21}(-3)$（即 $C_2=C_2-3C_1$）、$C_{31}(-4)$（即 $C_3=C_3-4C_1$）和 $C_{41}(-3)$（即 $C_4=C_4-3C_1$）：
   $$A\sim \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\end{array}\right]$$

Thus, $\text{Rank}(A)=2$, and $\text{Nullity}(A)=\text{Number of columns}-\text{Rank}=4-2=2$.
因此，$\text{Rank}(A)=2$，$\text{Nullity}(A)=\text{列数}-\text{秩}=4-2=2$。

Frequently Asked Questions on Rank and Nullity

关于秩与零化度的常见问题

Q1: What is the rank of the matrix?

问题 1：矩阵的秩是什么？

The number of linearly independent row or column vectors of a matrix is the rank of the matrix.
矩阵中线性无关的行向量或列向量的数量，称为矩阵的秩。

Q2: What is the nullity of the matrix?

问题 2：矩阵的零化度是什么？

The dimension of the nullspace or kernel of the given matrix is the nullity of the matrix.
给定矩阵的零空间（或核）的维数，称为矩阵的零化度。

Q3: What is the rank and nullity theorem for matrices?

问题 3：矩阵的秩-零化度定理是什么？

For any matrix $A$ of order $m\times n$, $\text{rank}(A)+\text{nullity}(A)=n$, where $n$ is the number of columns in $A$.
对于任意 $m\times n$ 阶矩阵 $A$，均有 $\text{rank}(A)+\text{nullity}(A)=n$（其中 $n$ 为 $A$ 的列数）。

Q4: What is the nullity of an invertible matrix?

问题 4：可逆矩阵的零化度是多少？
The nullity of an invertible matrix is zero.
可逆矩阵的零化度为 0。

---

The Rank-Nullity Theorem

秩-零化度定理

节选自 普渡大学数学系 2010 年春季学期的微分方程课程（MA26200）
Differential Equations and Linear Algebra by Stephen Goode and Scott A. Annin, Third Edition.Chapter 4.9

In Section 4.3, we defined the null space of a real $m\times n$ matrix $A$ to be the set of all real solutions to the associated homogeneous linear system $Ax=0$. Thus,
在第 4.3 节中，我们定义了实数 $m\times n$ 矩阵 $A$ 的零空间为与齐次线性方程组 $Ax=0$ 相关的所有实数解的集合。因此，
nullspace ( A ) = { x ∈ R n : A x = 0 } . \text{nullspace}(A) = \{ x \in \mathbb{R}^n : Ax = 0 \}. nullspace(A)={x∈Rn:Ax=0}.

The dimension of nullspace($A$) is referred to as the nullity of $A$ and is denoted $\text{nullity}(A)$.
零空间 ($A$) 的维度被称为 $A$ 的零化度，并记作 $\text{nullity}(A)$。

In order to find $\text{nullity}(A)$, we need to determine a basis for $\text{nullspace}(A)$. Recall that if $\text{rank}(A)=r$, then any row-echelon form of $A$ contains $r$ leading ones, which correspond to the bound variables in the linear system. Thus, there are $n-r$ columns without leading ones, which correspond to free variables in the solution of the system $Ax=0$. Hence, there are $n-r$ free variables in the solution of the system $Ax=0$. We might therefore suspect that $\text{nullity}(A)=n-r$. Our next theorem, often referred to as the Rank-Nullity Theorem, establishes that this is indeed the case.
为了找到 $\text{nullity}(A)$，我们需要确定 $\text{nullspace}(A)$ 的一个基。回忆一下，如果 $\text{rank}(A)=r$，那么 $A$ 的任何行阶梯形式都包含 $r$ 个主元，这些主元对应于线性系统中的绑定变量。因此，有 $n-r$ 列没有主元，这些对应于系统 $Ax=0$ 解中的自由变量。因此，在系统 $Ax=0$ 的解中有 $n-r$ 个自由变量。我们因此可能怀疑 $\text{nullity}(A)=n-r$。我们的下一个定理，通常称为秩-零化度定理，确立了这确实是这种情况。

Theorem 4.9.1 (Rank-Nullity Theorem)
定理 4.9.1（秩-零化度定理）

For any $m\times n$ matrix $A$,
对于任何 $m\times n$ 矩阵 $A$，

$$\text{rank}(A)+\text{nullity}(A)=n.$$

(4.9.1)

Proof If $\text{rank}(A)=n$, then by the Invertible Matrix Theorem, the only solution to $Ax=0$ is the trivial solution $x=0$. Hence, in this case, nullspace ( A ) = { 0 } \text{nullspace}(A) = \{0\} nullspace(A)={0}, so $\text{nullity}(A)=0$ and Equation (4.9.1) holds.
证明 如果 $\text{rank}(A)=n$，那么根据可逆矩阵定理，$Ax=0$ 的唯一解是平凡解 $x=0$。因此，在这种情况下， nullspace ( A ) = { 0 } \text{nullspace}(A) = \{0\} nullspace(A)={0}，所以 $\text{nullity}(A)=0$，方程 (4.9.1) 成立。

Now suppose $\text{rank}(A)=r<n$. In this case, there are $n-r>0$ free variables in the solution to $Ax=0$. Let $t_1,t_2,\dots ,t_{n-r}$ denote these free variables (chosen as those variables not attached to a leading one in any row-echelon form of $A$), and let $x_1,x_2,\dots ,x_{n-r}$ denote the solutions obtained by sequentially setting each free variable to 1 and the remaining free variables to zero. Note that { x 1 , x 2 , … , x n − r } \{x_1, x_2, \ldots, x_{n-r}\} {x1​,x2​,…,xn−r​} is linearly independent. Moreover, every solution to $Ax=0$ is a linear combination of $x_1,x_2,\dots ,x_{n-r}$:
现在假设 $\text{rank}(A)=r<n$。在这种情况下，$Ax=0$ 的解中有 $n-r>0$ 个自由变量。令 $t_1,t_2,\dots ,t_{n-r}$ 表示这些自由变量（选择为在 $A$ 的任何行阶梯形式中不与主元相连的变量），并令 $x_1,x_2,\dots ,x_{n-r}$ 表示通过依次将每个自由变量设为 1 并将其余自由变量设为 0 而得到的解。注意 { x 1 , x 2 , … , x n − r } \{x_1, x_2, \ldots, x_{n-r}\} {x1​,x2​,…,xn−r​} 是线性无关的。此外，$Ax=0$ 的每个解都是 $x_1,x_2,\dots ,x_{n-r}$ 的线性组合：

$$x=t_1{x}_1+t_2{x}_2+\cdots +t_{n-r}{x}_{n-r},$$

which shows that { x 1 , x 2 , … , x n − r } \{x_1, x_2, \ldots, x_{n-r}\} {x1​,x2​,…,xn−r​} spans $\text{nullspace}(A)$. Thus, { x 1 , x 2 , … , x n − r } \{x_1, x_2, \ldots, x_{n-r}\} {x1​,x2​,…,xn−r​} is a basis for $\text{nullspace}(A)$, and $\text{nullity}(A)=n-r$.
这表明 { x 1 , x 2 , … , x n − r } \{x_1, x_2, \ldots, x_{n-r}\} {x1​,x2​,…,xn−r​} 跨越了 $\text{nullspace}(A)$。因此， { x 1 , x 2 , … , x n − r } \{x_1, x_2, \ldots, x_{n-r}\} {x1​,x2​,…,xn−r​} 是 $\text{nullspace}(A)$ 的一个基，并且 $\text{nullity}(A)=n-r$。

Example 4.9.2
例 4.9.2

If
如果

$$A=\left[\begin{array}{cccc}1& 1& 2& 3\\ 3& 4& -1& 2\\ -1& -2& 5& 4\end{array}\right],$$

find a basis for $\text{nullspace}(A)$ and verify Theorem 4.9.1.
找到 $\text{nullspace}(A)$ 的一个基，并验证定理 4.9.1。

Solution We must find all solutions to $Ax=0$. Reducing the augmented matrix of this system yields
解 我们必须找到 $Ax=0$ 的所有解。将该系统的增广矩阵化简得到

$$A^{\#}\sim \left[\begin{array}{ccccc}1& 1& 2& 3& 0\\ 0& 1& -7& -7& 0\\ 0& -1& 7& 7& 0\end{array}\right]\sim \left[\begin{array}{ccccc}1& 1& 2& 3& 0\\ 0& 1& -7& -7& 0\\ 0& 0& 0& 0& 0\end{array}\right].$$

1. $A_{12}(-3)$, $A_{13}(1)$ 2. $A_{23}(1)$

Consequently, there are two free variables, $x_3=t_1$ and $x_4=t_2$, so that
因此，有两个自由变量，$x_3=t_1$ 和 $x_4=t_2$，使得

$$x_2=7t_1+7t_2,x_1=-9t_1-10t_2.$$

Hence,
因此，

n u l l s p a c e ( A ) = { ( − 9 t 1 − 10 t 2 , 7 t 1 + 7 t 2 , t 1 , t 2 ) : t 1 , t 2 ∈ } = { t 1 ( − 9 , 7 , 1 , 0 ) + t 2 ( − 10 , 7 , 0 , 1 ) : t 1 , t 2 ∈ } = s p a n { ( − 9 , 7 , 1 , 0 ) , ( − 10 , 7 , 0 , 1 ) } . \begin{array}{lll} {\rm{nullspace}}(A) & = \{ ( - 9{t_1} - 10{t_2},7{t_1} + 7{t_2},{t_1},{t_2}):{t_1},{t_2} \in \} \\ & = \{ {t_1}( - 9,7,1,0) + {t_2}( - 10,7,0,1):{t_1},{t_2} \in \} \\ & = {\rm{span}}\{ ( - 9,7,1,0),( - 10,7,0,1)\} . \end{array} nullspace(A)​={(−9t1​−10t2​,7t1​+7t2​,t1​,t2​):t1​,t2​∈}={t1​(−9,7,1,0)+t2​(−10,7,0,1):t1​,t2​∈}=span{(−9,7,1,0),(−10,7,0,1)}.​

Since the two vectors in this spanning set are not proportional, they are linearly independent. Consequently, a basis for $\text{nullspace}(A)$ is $\{(-9,7,1,0),(-10,7,0,1)\}$, so that $\text{nullity}(A)=2$. In this problem, $A$ is a $3\times 4$ matrix, and so, in the Rank-Nullity Theorem, $n=4$. Further, from the foregoing row-echelon form of the augmented matrix of the system $Ax=0$, we see that $\text{rank}(A)=2$. Hence,
由于该生成集中的两个向量不成比例，它们是线性无关的。因此，$\text{nullspace}(A)$ 的一个基是 $\{(-9,7,1,0),(-10,7,0,1)\}$，所以 $\text{nullity}(A)=2$。在这个问题中，$A$ 是一个 $3\times 4$ 矩阵，因此，在秩-零化度定理中，$n=4$。此外，从系统 $Ax=0$ 的增广矩阵的行阶梯形式中，我们看到 $\text{rank}(A)=2$。因此，
$$\text{rank}(A)+\text{nullity}(A)=2+2=4=n,$$

and the Rank-Nullity Theorem is verified.
并且秩-零化度定理得到了验证。

---

秩-零化度定理（Rank-Nullity Theorem）

MatNoble 编辑于 2020-02-09 08:16

引言

线性代数（高等代数） 与 微积分（数学分析） 存在差异，线性代数是一门持续发展的学科。其在实际应用中产生的新问题会反哺教学，而教学的进步又能进一步推动实际应用的发展。

秩-零化度定理（Rank-Nullity Theorem）

如图 1 所示，线性变换 $T$ 从有限维向量空间 $\mathcal{V}$（定义域）映射到有限维向量空间 $\mathcal{W}$（值域），记为 $T:\mathcal{V}\to \mathcal{W}$。

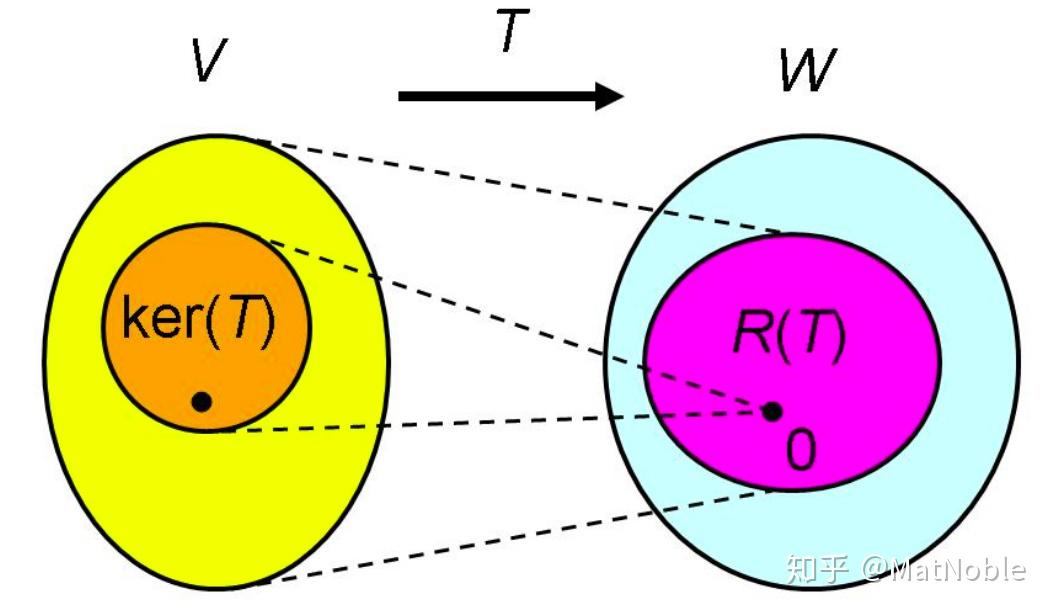
图 1 线性变换 $T:\mathcal{V}\to \mathcal{W}$ 的示意图

在该映射关系中，存在两个重要的子空间，分别定义如下：

1. 核空间（Kernel Space）

向量空间 $\mathcal{V}$ 中所有经线性变换 $T$ 映射后得到零元素的元素所构成的集合，称为 $T$ 的核（子）空间，记为 $\ker (T)$。
核空间的维数（dimension）称为零化度（nullity），记为 $\dim \ker (T)$，用于度量核空间的规模。

2. 值域（Range）

向量空间 $\mathcal{V}$ 中所有元素经线性变换 $T$ 映射后所构成的集合，称为 $T$ 的值域，记为 $\mathrm{ran}(T)$ 或 $R(T)$。
值域的维数（dimension）称为秩（rank），记为 $\mathrm{rank}T$ 或 $\dim \mathrm{ran}(T)$。

秩-零化度定理的表述

线性变换 $T:\mathcal{V}\to \mathcal{W}$ 的定义域 $\mathcal{V}$ 的维数，等于其核空间 $\ker (T)$ 的维数与值域 $\mathrm{ran}(T)$ 的维数之和，即：
$$\dim \mathcal{V}=\dim \ker (T)+\mathrm{rank}T$$

秩-零化度定理的证明

秩-零化度定理可从矩阵角度与线性变换角度分别证明，两种证明思路各有侧重，共同支撑定理的严谨性。

1. 矩阵角度的证明

线性变换可通过矩阵具象化表示，因此可借助矩阵的零空间与列空间证明定理。

步骤 1：设定基本条件

设线性变换 $T:\mathcal{V}\to \mathcal{W}$ 由 $m\times n$ 阶矩阵 $A$ 表示，其中：

• $n=\dim \mathcal{V}$（定义域 $\mathcal{V}$ 的维数）；
• $m=\dim \mathcal{W}$（值域 $\mathcal{W}$ 的维数）；
• 矩阵 $A$ 的零空间 $N(A)$ 对应线性变换 $T$ 的核空间 $\ker (T)$；
• 矩阵 $A$ 的列空间 $C(A)$ 对应线性变换 $T$ 的值域 $\mathrm{ran}(T)$。

需证明的结论转化为：
$$n=\dim N(A)+\mathrm{rank}A$$

步骤 2：矩阵的初等行变换化简

对矩阵 $A$ 进行初等行变换，可将其化为如下分块矩阵形式：
$$R=\left[\begin{array}{cc}{E}_r& F\\ 0& 0\end{array}\right]$$
其中：

• $E_r$ 为 $r$ 阶单位矩阵；
• $F$ 为 $r\times (n-r)$ 阶矩阵；
• 矩阵 $R$ 的秩为 $r$，即 $\mathrm{rank}R=r$。

由于初等行变换不改变矩阵的秩与零空间，因此有：

• $\mathrm{rank}A=\mathrm{rank}R=r$；
• $N(A)=N(R)$（矩阵 $A$ 与 $R$ 的零空间相同）。

步骤 3：构造零空间矩阵并验证

观察分块矩阵 $R$，构造其 $n\times (n-r)$ 阶零空间矩阵 $P$：
$$P=\left[\begin{array}{c}-F\\ E_{n-r}\end{array}\right]$$
其中 $E_{n-r}$ 为 $(n-r)$ 阶单位矩阵。

验证 $P$ 满足零空间定义（即 $RP=0$）：
$$RP=\left[\begin{array}{cc}{E}_r& F\\ 0& 0\end{array}\right]\left[\begin{array}{c}-F\\ E_{n-r}\end{array}\right]=\left[\begin{array}{c}-F+F\\ 0\end{array}\right]=0$$

步骤 4：证明 $C(P)=N(R)$

• 首先，矩阵 $P$ 的秩 $\mathrm{rank}P=n-r$，说明其列向量线性无关；
• 其次，任取 $x\in N(R)$（即 $Rx=0$），将 $x$ 按分块形式表示为 $x=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$，其中 $x_1$ 为 $r$ 维向量，$x_2$ 为 $(n-r)$ 维向量。代入 $Rx=0$ 得：
  $$Rx=\left[\begin{array}{cc}{E}_r& F\\ 0& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}{x}_1+F{x}_2\\ 0\end{array}\right]=0$$
  由此推出 $x_1=-F{x}_2$，进而有：
  $$x=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}-F{x}_2\\ x_2\end{array}\right]=\left[\begin{array}{c}-F\\ E_{n-r}\end{array}\right]x_2=P{x}_2$$
  即 $x$ 可由 $P$ 的列向量线性表出。

综上，$C(P)=N(R)$，因此 $\dim N(A)=\dim N(R)=\mathrm{rank}P=n-r$。代入 $\mathrm{rank}A=r$，得：
$$n=\dim N(A)+\mathrm{rank}A$$
矩阵角度的证明完成。

2. 线性变换角度的证明

线性变换的核心是“保持线性运算”，可通过基底的映射关系证明定理。

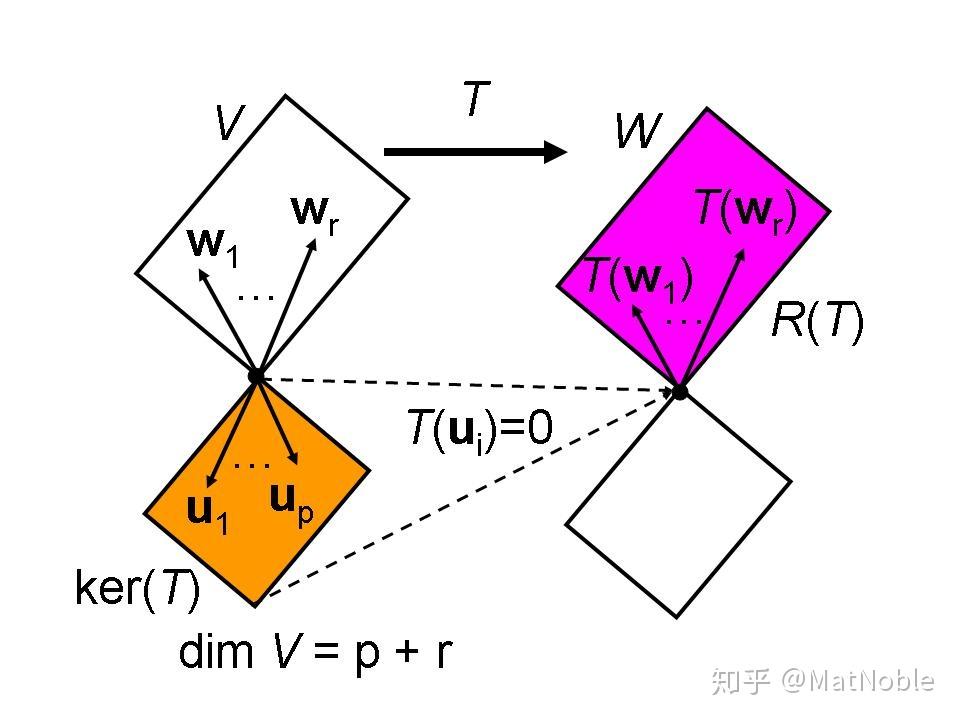
步骤 1：设定基本条件与基底扩充

设向量空间 $\mathcal{V}$ 的维数 $\dim \mathcal{V}=n$，线性变换 $T$ 的核空间维数 $\dim \ker (T)=p$（显然 $p\le n$）。
取 $\ker (T)$ 的一组基底 { u 1 , u 2 , … , u p } \{u_1, u_2, \dots, u_p\} {u1​,u2​,…,up​}，将其扩充为 $\mathcal{V}$ 的一组基底：
{ u 1 , u 2 , … , u p , w 1 , w 2 , … , w r } \{u_1, u_2, \dots, u_p, w_1, w_2, \dots, w_r\} {u1​,u2​,…,up​,w1​,w2​,…,wr​}
其中 $n=p+r$。需证明的结论转化为：
$$\mathrm{rank}T=r$$

步骤 2：分析任意向量的像

对 $\mathcal{V}$ 中任意向量 $v$，由基底的线性表示性质，可将其表示为：
$$v=a_1{u}_1+a_2{u}_2+\cdots +a_p{u}_p+b_1{w}_1+b_2{w}_2+\cdots +b_r{w}_r$$
其中 $a_1,\dots ,a_p,b_1,\dots ,b_r$ 为常数。

对 $v$ 施加线性变换 $T$，根据线性变换的性质（可加性、齐次性），其像 $T(v)$ 满足：
$$\begin{array}{rl}T(v)& =T\left(a_1{u}_1+\cdots +a_p{u}_p+b_1{w}_1+\cdots +b_r{w}_r\right)\\ & =a_{1}T(u_1)+\cdots +a_{p}T(u_p)+b_{1}T(w_1)+\cdots +b_{r}T(w_r)\end{array}$$
由于 $u_1,\dots ,u_p\in \ker (T)$，故 $T(u_1)=\cdots =T(u_p)=0$，因此：
$$T(v)=b_{1}T(w_1)+b_{2}T(w_2)+\cdots +b_{r}T(w_r)$$
这表明 $T(v)$ 可由 { T ( w 1 ) , … , T ( w r ) } \{T(w_1), \dots, T(w_r)\} {T(w1​),…,T(wr​)} 线性表示，即 $\mathrm{ran}T$ 可由该向量组张成。

步骤 3：证明基底的线性无关性

只需证明 { T ( w 1 ) , T ( w 2 ) , … , T ( w r ) } \{T(w_1), T(w_2), \dots, T(w_r)\} {T(w1​),T(w2​),…,T(wr​)} 线性无关，即可确认其为 $\mathrm{ran}T$ 的一组基底（维数为 $r$）。

假设存在常数 $c_1,c_2,\dots ,c_r$，使得：
$$c_{1}T(w_1)+c_{2}T(w_2)+\cdots +c_{r}T(w_r)=0$$
根据线性变换的性质，上式可改写为：
$$T\left(c_1{w}_1+c_2{w}_2+\cdots +c_r{w}_r\right)=0$$
这表明 $c_1{w}_1+\cdots +c_r{w}_r\in \ker (T)$。由于 { u 1 , … , u p } \{u_1, \dots, u_p\} {u1​,…,up​} 是 $\ker (T)$ 的基底，故存在常数 $d_1,\dots ,d_p$，使得：
$$c_1{w}_1+\cdots +c_r{w}_r=d_1{u}_1+\cdots +d_p{u}_p$$
整理得：
$$d_1{u}_1+\cdots +d_p{u}_p-c_1{w}_1-\cdots -c_r{w}_r=0$$
由于 { u 1 , … , u p , w 1 , … , w r } \{u_1, \dots, u_p, w_1, \dots, w_r\} {u1​,…,up​,w1​,…,wr​} 是 $\mathcal{V}$ 的基底（线性无关），故所有系数均为零，即 $c_1=\cdots =c_r=0$。

因此， { T ( w 1 ) , … , T ( w r ) } \{T(w_1), \dots, T(w_r)\} {T(w1​),…,T(wr​)} 线性无关，即 $\mathrm{rank}T=r$。结合 $n=p+r$ 与 $p=\dim \ker (T)$，得：
$$\dim \mathcal{V}=\dim \ker (T)+\mathrm{rank}T$$
线性变换角度的证明完成。

秩-零化度定理的推论

基于秩-零化度定理，可推导出关于线性变换“非零核”与“非满射”的重要结论，也可转化为矩阵语言表述。

推论 1：定义域维数大于值域维数时，存在非零核

若 $\dim \mathcal{V}>\dim \mathcal{W}$，由秩-零化度定理 $\dim \ker (T)=\dim \mathcal{V}-\dim \mathrm{ran}(T)$，结合 $\dim \mathrm{ran}(T)\le \dim \mathcal{W}$，得：
$$\dim \ker (T)\ge \dim \mathcal{V}-\dim \mathcal{W}>0$$
这表明 $\ker (T)$ 中存在非零向量，即存在 $\mathbf{x}\in \mathcal{V}$（$\mathbf{x}\ne 0$），使得 $T(\mathbf{x})=0$。

推论 2：定义域维数小于值域维数时，变换非满射

若 $\dim \mathcal{V}<\dim \mathcal{W}$，由秩-零化度定理 $\dim \mathrm{ran}(T)=\dim \mathcal{V}-\dim \ker (T)$，结合 $\dim \ker (T)\ge 0$，得：
$$\dim \mathrm{ran}(T)\le \dim \mathcal{V}<\dim \mathcal{W}$$
这表明 $\mathrm{ran}(T)$ 是 $\mathcal{W}$ 的真子空间，即存在 $\mathbf{y}\in \mathcal{W}$，使得 $\mathbf{y}\notin \mathrm{ran}(T)$，线性变换 $T$ 不是满射。

推论的矩阵语言表述

设矩阵 $A$ 为 $m\times n$ 阶矩阵，对应线性变换 $T:\mathcal{V}\to \mathcal{W}$（$\dim \mathcal{V}=n$，$\dim \mathcal{W}=m$），则推论可转化为：

1. 当 $n>m$（“矮胖”矩阵）时

由 $\dim N(A)=n-\dim C(A)$ 与 $\dim C(A)\le m$，得：
$$\dim N(A)\ge n-m>0$$
即矩阵 $A$ 的零空间 $N(A)$ 包含非零向量，齐次线性方程组 $A\mathbf{x}=0$ 有无限多组解。

图 2 “矮胖”矩阵（$n>m$）的零空间示意图

2. 当 $n<m$（“瘦高”矩阵）时

由 $\dim C(A)=n-\dim N(A)$ 与 $\dim N(A)\ge 0$，得：
$$\dim C(A)\le n<m$$
即矩阵 $A$ 的列空间 $C(A)$ 无法充满整个 ${\mathbb{R}}^m$，非齐次线性方程组 $A\mathbf{x}=b$ 可能无解。

图 3 “瘦高”矩阵（$n<m$）的列空间示意图

---

列空间与零空间，秩—零化度定理

_Equinox 已于 2025-07-27 09:34:02 修改

1. 向量空间的封闭性

任取空间内 $\overrightarrow{A}$ 和 $\overrightarrow{B}$，且 $\overrightarrow{A}\ne k\overrightarrow{B}$，满足 $l_1\overrightarrow{A}+l_2\overrightarrow{B}$ 仍在空间内。

2. 列空间

The short useful word “span” describes all the linear combinations of a set of vectors. So the span of the columns of A (independent or not) is the column space.
“Span” 这个简短而有用的词汇描述了一组向量的所有线性组合。因此，矩阵 A 的列向量的张成（无论是否线性无关）构成了列空间。

张成（span）：一个向量集合的所有线性组合。矩阵 $A$ 的列向量的张成，即矩阵 $A$ 的列空间（column space）。

线性方程组的意义在于：对于矩阵 $A$ 和向量 $B$，方程 $AX=B$ 有解当且仅当 $B$ 在 $A$ 的列空间内，即 $B\in C(A)$。

例如，矩阵 $A$ 为
$$A=\left[\begin{array}{ccc}1& 1& 2\\ 2& 1& 3\\ 3& 1& 4\\ 4& 1& 5\end{array}\right]=\left[\begin{array}{ccc}{c}_1& c_2& c_3\end{array}\right],C(A)\subset {\mathbb{R}}^4$$
对于方程组 $AX=B$，有解：

当且仅当 $B=k_1{c}_1+k_2{c}_2+k_3{c}_3$，即 $B$ 在 $A$ 的列空间内，$B\in C(A)$。

因此，方程 $AX=B$ 有解 <=> $B$ 在 $A$ 的列空间内。

3. 零空间

The nullspace $N(A)$ in ${\mathbb{R}}^n$ contains all solutions $x$ to $Ax=0$. This includes $x=0$.
零空间 $N(A)$ 在 ${\mathbb{R}}^n$ 中包含所有满足 $Ax=0$ 的解 $x$。这包括 $x=0$。

矩阵 $A$ 的零空间是所有满足 $AX=0$ 的解向量的集合。显然，零向量一定属于零空间。

4. I F 型

考虑矩阵
$$\left[\begin{array}{cccc}1& 7& 0& 8\\ 0& 0& 1& 9\end{array}\right]x=\left[\begin{array}{c}0\\ 0\end{array}\right]$$
其解向量为
$$x=\left[\begin{array}{c}-7\\ 1\\ 0\\ 0\end{array}\right],x=\left[\begin{array}{c}-8\\ 0\\ -9\\ 1\end{array}\right]$$
或者可以写成矩阵形式
$$\left[\begin{array}{cc}-7& -8\\ 1& 0\\ 0& -9\\ 0& 1\end{array}\right]$$

为了更直观地表示，可以施加一个置换矩阵 $P$，使得
$$P{P}^T=I$$
则
$$\begin{array}{rl}\left[\begin{array}{cccc}1& 7& 0& 8\\ 0& 0& 1& 9\end{array}\right]P{P}^T\left[\begin{array}{cc}-7& -8\\ 1& 0\\ 0& -9\\ 0& 1\end{array}\right]& =\left[\begin{array}{cccc}1& 7& 0& 8\\ 0& 0& 1& 9\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cc}-7& -8\\ 1& 0\\ 0& -9\\ 0& 1\end{array}\right]\\ & =\left[\begin{array}{cccc}1& 0& 7& 8\\ 0& 1& 0& 9\end{array}\right]\left[\begin{array}{cc}-7& -8\\ 1& 0\\ 0& -9\\ 0& 1\end{array}\right]\\ & =\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\\ 0& 0\end{array}\right]\end{array}$$

更一般地，对于 $AX=0$，可以对 $AX=0$ 施加高斯消元法，转换成如下形式：
$$\left[\begin{array}{cc}I& F\end{array}\right]P{P}^{T}x=0$$
其中 $I$ 为单位阵，$P$ 为置换阵。解向量可以表示为
$$\left[\begin{array}{c}-F\\ I\end{array}\right]$$

事实上，这对应了高斯消元化为阶梯型后的主元和自由元。

由于 $r(I)=r(A)$，可以得到 $r(F)=n-r(A)$。

矩阵 $A$ 的零空间的维度正是 $n-r(A)$。

5. 秩—零化度定理

秩—零化度定理（Rank–Nullity Theorem） 表示有限维向量空间上线性变换 $T:V\to W$ 定义空间的维数 $\text{dim}V$ 等于核空间的维数加上像空间的维数。

对于矩阵变换 $T(x)=Ax$ 即列数 $n$ 等于零空间的维数加上列空间的维数，对于对偶映射 $T(x)=A^{T}x$ 即行数 $m$ 等于左零空间的维数加上行空间的维数，值域维数即矩阵的秩

• $\text{dim}V=\text{dim Ker}(T)+\text{dim Im}(T)$
• $n=\text{dim Nul}A+\text{dim Col}A$
• $m=\text{dim Nul}{A}^T+\text{dim Row}A$

对于任意 $n\times n$ 矩阵 $A$，有
$$r(A)+r(N(A))=n$$

根据该定理可以得出一些有关秩的关系式：

1. 对于 $n$ 阶方阵 $A$ 和 $B$，若 $AB=0$，则 $r(A)+r(B)\le n$

   证明：
   $$AB=0\Rightarrow C(B)\subset N(A)\Rightarrow r(B)\le n-r(A)\Rightarrow r(A)+r(B)\le n$$

2. $r(A^{T}A)=r(A)$

   证明：
   $$A^{T}Ax=0\iff x^T{A}^{T}Ax=0\iff \Vert Ax{\Vert }^2=0\iff Ax=0$$
   因此，$N(A^{T}A)=N(A)$，从而 $r(A^{T}A)=r(A)$。

3. $r(A^{\ast })$ 与 $r(A)$ 的关系

   • 当 $r(A)=n$ 时（$A$ 为满秩/可逆矩阵）：$A^{\ast }$ 也是满秩的，即 $r(A^{\ast })=n$。
   • 当 $r(A)=n-1$ 时：$A^{\ast }$ 的秩为 1，即 $r(A^{\ast })=1$。
   • 当 $r(A)<n-1$ 时：$A^{\ast }$ 是零矩阵，即 $r(A^{\ast })=0$。

   证明：

   • 当 $r(A)=n$ 时：
     $$A{A}^{\ast }=|A|I$$
     因此，$A^{\ast }$ 可逆，$r(A^{\ast })=n$。
   • 当 $r(A)=n-1$ 时：
     $$A{A}^{\ast }=0\Rightarrow C(A^{\ast })\subset N(A)\Rightarrow r(A^{\ast })\le r(N(A))=1$$
     又因为 $r(A^{\ast })\ge 1$，由夹逼定理可知，$r(A^{\ast })=1$。
   • 当 $r(A)<n-1$ 时：
     根据 $A^{\ast }$ 的定义，因为 $r(A)<n-1$，所以 $A$ 的所有 $n-1$ 阶子式均为 0，因此 $A^{\ast }=0$。

4. $r(A^{T}A)=r(A)$ 且 $C(A^{T}A)=C(A)$

   证明：

$$\begin{array}{lll}Ax=0& \Rightarrow & A^{T}Ax=0\\ & \Rightarrow & C(A)\subset C(A^{T}A)\end{array}$$

$$\begin{array}{lll}{A}^{T}Ax=0& \Rightarrow & x^T{A}^{T}Ax=0\\ & \Rightarrow & (Ax{)}^T(Ax)=0\\ & \Rightarrow & Ax=0\\ & \Rightarrow & C(A^{T}A)\subset C(A)\end{array}$$

因此，$C(A^{T}A)=C(A)$，从而 $r(A)=r(A^{T}A)$。

---

via：

• byjus.com/maths/rank-and-nullity/
  https://byjus.com/maths/rank-and-nullity/
• The Rank-Nullity Theorem C:GOODEMAIN.DVI - 4-9.pdf
  https://www.math.purdue.edu/files/academic/courses/2010spring/MA26200/4-9.pdf
• 「秩-零化度定理」(Rank-Nullity Theorem) - 知乎
  https://zhuanlan.zhihu.com/p/102521072
• 列空间与零空间，秩—零化度定理_列空间和零空间-优快云博客 …
  https://blog.youkuaiyun.com/EQUINOX1/article/details/149491205