Transformer | the L-Mul operation in tensor processing hardware can potentially reduce 95% energy

注：两篇关于 L-Mul 算法的文章。

---

LLM 合集：L-Mul 算法 – 在 Transformer 中以整数加法替代乘法，节省高达 95% 算力

原创 AI-PaperDaily

1. Addition is All You Need for Energy-efficient Language Models

  ~  
  ~  

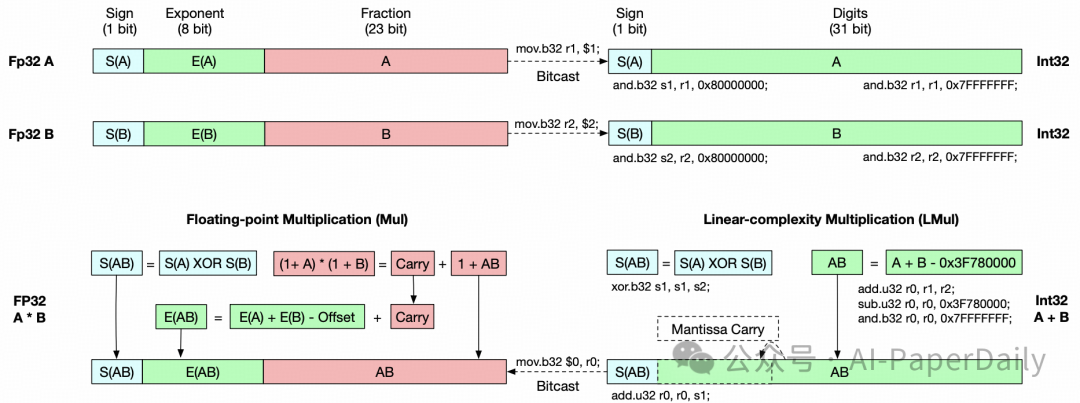
大型神经网络在大多数计算中用于浮点张量乘法。在本文中，我们发现浮点乘法可以由一个高精度的整数加法器近似。我们提出了线性复杂度乘法 L-Mul 算法，该算法使用整数加法运算近似浮点数乘法。与 8 位浮点乘法相比，新算法消耗的计算资源显著减少，但精度更高。由于浮点数乘法比整数加法消耗更多算力，将 L-Mul 操作应用于张量处理硬件可以潜在地减少 95% 的元素级浮点张量乘法算力成本和 80% 的点积算力成本。

我们计算了 L-Mul 的理论误差期望值，并在包括自然语言理解、结构推理、数学和常识问答在内的广泛文本、视觉和符号任务上评估了该算法。我们分析实验与理论误差估计相符，表明具有 4 位尾数的 L-Mul 与 float8_e4m3 乘法具有可比精度，而具有 3 位尾数的 L-Mul 优于 float8_e5m2。在流行基准上的评估结果表明，直接将 L-Mul 应用于注意力机制几乎是无损失的。我们进一步证明，在 transformer 模型中用 3 位尾数的 L-Mul 替换所有浮点乘法操作，与使用 float8_e4m3 作为累积精度的浮点数乘法在微调和推理中具有同等精度。

论文: https://arxiv.org/pdf/2410.00907

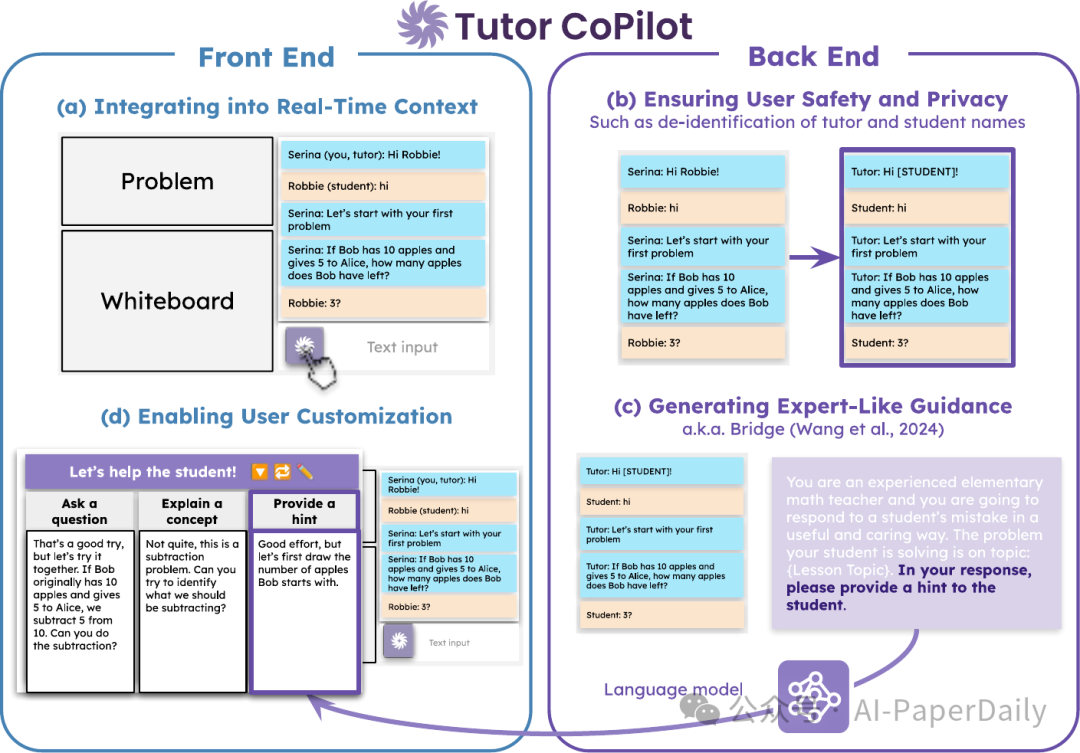
2. Tutor CoPilot: A Human-AI Approach for Scaling Real-Time Expertise

  ~  
  ~  

生成式 AI，特别是语言模型（LMs），有潜力改变现实世界的应用领域，特别是在专家资源有限的领域。例如，在教育方面，用专家指导来培训新手教师至关重要，但成本高昂，从而在大规模提高教育质量方面形成重大障碍。这一挑战不成比例地影响了来自未服务社区的学生，他们最能从高质量教育中获益。我们介绍了 Tutor CoPilot，这是一种创新的人工智能方法，利用专家思维模型为辅导者提供类似专家的指导。这是首次在实时辅导中进行的人工智能系统的随机对照试验，涉及 900 名辅导者和 1,800 名来自历史上未服务社区的 K-12 学生。按照预先注册的分析方案，我们发现使用 Tutor CoPilot 的辅导者的学生更有可能掌握知识点（增加了 4 个百分点，p<0.01）。值得注意的是，低评价辅导者的学生成为最大受益者，提高掌握程度 9 个百分点。我们发现 Tutor CoPilot 每年每辅导者仅需 20 美元。我们分析了超过 550,000 条消息，使用分类器识别教学策略，并发现使用 Tutor CoPilot 的辅导者更有可能使用高质量策略来促进学生理解（例如，提出引导性问题），且更不可能直接告诉答案。辅导者访谈强调了 Tutor CoPilot 如何帮助辅导者回应学生需求，尽管他们指出了一些问题，如生成不合适的年级水平的建议。

论文: https://arxiv.org/pdf/2410.03017

3. NL-Eye: Abductive NLI for Images

  ~  
  ~  

基于视觉语言模型（VLM）的机器人是否会警告我们地板湿滑可能会滑倒？最近的 VLM 展示了令人印象深刻的性能，但它们推断结果和原因的能力仍然有待探索。为了解决这个问题，我们引入了 NL-Eye，一个旨在评估 VLM 视觉演绎推理能力的基准。NL-Eye 将演绎自然语言推理（NLI）任务改编到视觉领域，要求模型根据前提图像评估假设图像的合理性，并解释其决策。NL-Eye 包含 350 个精心策划的三元组示例（1050 张图像），涵盖多种推理类别：物理、功能、逻辑、情感、文化和社会。数据策划过程包括两个步骤 —— 编写文本描述和使用文本到图像模型生成图像，两者都需要大量的人工参与以确保高质量和具有挑战性的场景。我们的实验表明，VLM 在 NL-Eye 上的表现显著困难，经常表现得像随机基线水平，而人类在合理性判断和解释质量方面表现出色。这表明现代 VLM 在演绎推理能力方面存在缺陷。NL-Eye 代表了朝着开发适用于现实世界应用的稳健多模态推理能力的 VLM 的重要一步，包括事故预防机器人和生成视频验证。

论文: https://arxiv.org/pdf/2410.02613

4. Accelerating Auto-regressive Text-to-Image Generation with Training-free Speculative Jacobi Decoding

  ~  
  ~  

当前的大型自回归模型可以生成高质量、高分辨率的图像，但在推理过程中，这些模型需要数百甚至数千步的下一个 token 预测，导致显著的时间消耗。在现有研究中，雅可比解码是一种迭代并行解码算法，已被用于加速自回归生成，并且可以在不进行训练的情况下执行。然而，雅可比解码依赖于确定性的标准来判断迭代的收敛性。因此，它适用于贪婪解码，但与当前自回归文本到图像生成中至关重要的基于采样的解码不兼容，后者对于视觉质量和多样性至关重要。在本文中，我们提出了一种无需训练的概率并行解码算法 —— 推测性雅可比解码（SJD），以加速自回归文本到图像生成。通过引入概率收敛标准，我们的 SJD 在保持基于采样的 token 解码的随机性的同时加速了自回归文本到图像生成的推理过程，并允许模型生成多样性的图像。具体来说，SJD 使模型能够在每一步预测多个 token，并基于概率标准接受这些 token，从而使模型能够生成比传统的下一个 token 预测范式所需的步骤更少的图像。我们还研究了利用视觉数据的空间局部性来进一步提高加速比的 token 初始化策略，以在特定场景下进一步提高加速效果。我们在多个自回归文本到图像生成模型上进行了 SJD 的实验，证明了在不牺牲视觉质量的情况下模型加速的有效性。

论文: https://arxiv.org/pdf/2410.01699

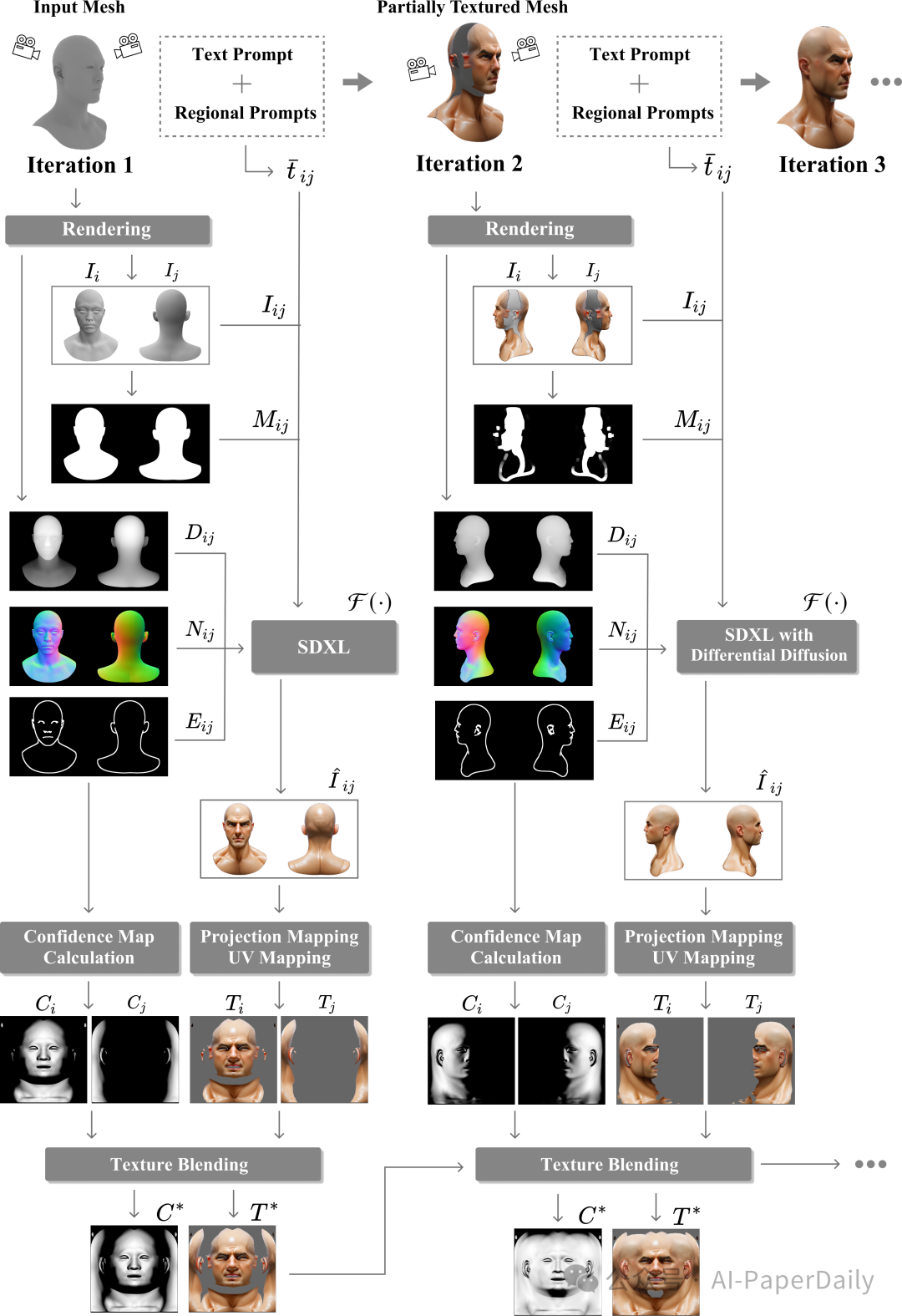
5. RoCoTex: A Robust Method for Consistent Texture Synthesis with Diffusion Models

  ~  
  ~  

文本生成纹理最近引起了越来越多的关注，但现有方法往往受到视角不一致、明显接缝以及纹理与底层网格对齐不良等问题的困扰。在本文中，我们提出了一种稳健的文本生成纹理方法，用于生成一致且无缝的纹理，且与网格对齐良好。该方法采用了最新的 2D 扩散模型，包括 SDXL 和多个 ControlNets，以捕捉生成纹理中的结构特征和精细细节。该方法还采用了对称视角合成策略，并结合了区域提示以增强视角一致性。此外，它引入了新颖的纹理混合和软修复技术，显著减少了接缝区域。大量实验表明，我们的方法优于现有的最先进的方法。

论文: https://arxiv.org/pdf/2409.19989

6. Selective Attention Improves Transformer

  ~  
  ~  

不必要的元素会降低注意力机制的性能。我们引入了选择性注意力，这是一种简单的无参数变化，可以减少对不必要的元素的关注。选择性注意力在各种模型大小和上下文长度的语言建模中表现更好。例如，使用语言建模目标在 C4 上训练的一系列 transformer，在选择性注意力的作用下，其性能与标准 transformer 相当，后者在注意力模块中有大约 2 倍更多的头和参数。选择性注意力还允许减少注意力上下文缓冲区的大小，从而在推理期间显著减少内存和计算需求。例如，使用 C4 训练的参数量为 100M 的 transformer，在上下文大小分别为 512、1024 和 2048 的情况下，配备选择性注意力后，其注意力模块所需的内存分别比没有选择性注意力的相同验证困惑度情况下少 16 倍、25 倍和 47 倍。

论文: https://arxiv.org/pdf/2410.02703

---

「乘法变加法」！MIT 清华校友全新方法优化 Transformer：Addition is All You Need

原创 新智元 编辑：乔杨 好困

【新智元导读】 Transformer 计算，竟然直接优化到乘法运算了。MIT 两位华人学者近期发表的一篇论文提出：Addition is All You Need，让 LLM 的能耗最高降低 95%。

LLM 能耗的疯狂增长，甚至已经引起了联合国的注意，成为了不容小觑的能源消耗者。

据统计，2023 年初 ChatGPT 服务的平均用电量为每天 564 兆瓦时，相当于 18000 个美国家庭每天的总用电量。

谷歌的情况更加严峻。最坏的情况下，谷歌 AI 服务消耗的电力可能和一整个爱尔兰相当，约为每年 29.3 TWh。
  ~  
  ~  

要在提升推理速度的同时降低大模型的能耗，减少神经网络所需的计算量才是关键。

而 LLM 等大规模神经网络，大部分计算量正是消耗在浮点级精度的矩阵乘法上。

从线性注意力机制到量化，大多数 Transformer 的优化都离不开对于乘法效率的大幅提高。要么减少运算操作次数，要么减少操作数的位数。

但如果从乘法运算这个更加底层的逻辑出发，两位华人研究者提出，可以用一个整数加法器以高精度近似进行浮点数乘法运算，即 L-Mul 乘法算法。
  ~  
  ~  

论文地址：https://arxiv.org/abs/2410.00907

相比量化过程中的 FP8 乘法，L-Mul 能达到更高的精度，而且运算量显著减少。

实验结果显示，在张量处理硬件中应用 L-Mul 操作能将逐元素浮点张量乘法的能量成本降低 95%，点积的能量成本降低 80%。

此外，L-Mul 可以直接集成到各个级别的现有模型中，无需额外训练，甚至能无损替换注意力机制中所有的矩阵、元素级别的浮点数乘法。
  ~  
  ~  

整体而言，L-Mul 方法专注于提高对张量进行算术运算的效率 —— 这与当前在 I/O 和控制优化方面的研究是相互独立但又相辅相成的。

由此作者认为，真正高能效、高计算效率的人工智能计算将从 I/O、控制流，和算术运算的全面优化整合中产生。

论文简介

大多数机器学习模型，包括神经网络，都使用浮点张量来表示它们的输入、输出和可训练参数。

其中，典型的选择是 32 位和 16 位浮点张量，即 fp32 和 fp16。
  ~  
  ~  

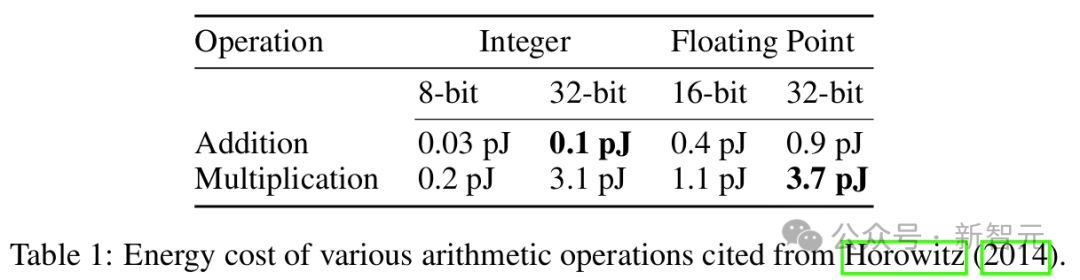
在现代计算硬件中，浮点数之间的乘法比加法运算消耗更多的能量，浮点数运算也显然比整数更加昂贵。

用 n 代表数字位数，那么整数加法的计算复杂度仅有 O (n)；而对于指数部分有 e 位、尾数部分有 m 位的浮点数，乘法运算则需要 O (e) 复杂度的加法加上 O (m^2) 复杂度的乘法。
  ~  
  ~  

如表 1 所示，元素级别的运算上，fp32 乘法和 int32 加法已经差距悬殊，能量高出 37 倍；如果是张量级别的运算，那更是相差甚远。

比如下面两种常用的运算：逐元素乘法 Y_1 和点积 Y_2。
  ~  

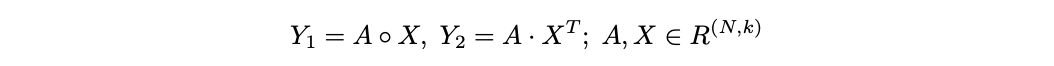
计算 Y_1 时，如果 A 和 X 都是 fp32 张量，相比 int32 矩阵的加法所消耗的能量也会高出 37 倍。

同样，计算 Y_2 时涉及 m×n×k 次的浮点乘法和加法，两个数字的每次乘加运算都会消耗 0.9+3.7=4.6（pJ）能量。

如果替换为 int32，那么每次运算的能量成本就变为 0.1+0.9=1.0 pJ，仅为原始成本的 21.7%。

类似地，如果原始精度为 fp16，替换为 int16 后也能达到 1−(0.05+0.4)/(1.1+0.4)=70% 的效率提升。

线性复杂度乘法（L-MUL）

那么，对于 n 位的浮点数，到底要如何用整数加法近似计算浮点数乘法，实现 O (n) 复杂度？

考虑两个浮点数 x 和 y，它们的指数和小数部分的位数分别为 x_e、y_e 和 x_m、y_m。

传统的浮点乘法可以表示为：
  ~  
  ~  

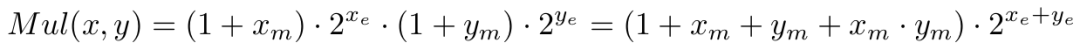再加上一个异或操作（⊕）来决定结果的符号为正或为负。

其中，尾数部分的乘法操作是提升效率的瓶颈，复杂度为 O (m^2)。

L-Mul 所做的，就是移除这个操作，引入了一种新的乘法算法，以 O (m) 的计算复杂度处理尾数：
  ~  
  ~  

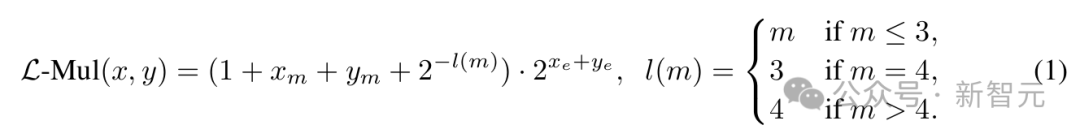对比上面的公式可以发现，我们仅仅是将 x_m・y_m 替换为 2^{-l⁢(m)}，其中 l (m) 是一个简单的分段函数。

虽然等式 (1) 包含 4 个加法操作，但浮点数的位格式设计能帮助我们用一个加法器实现 L-Mul 算法。

浮点格式隐式处理 1+x_m，所以不必计算 (1+…) 的值；整数加法操作还会自动将尾数进位发送到指数，这与传统浮点乘法器中的舍入过程不同。

在传统方法中，小数部分需要手动舍入为 1.x，并且向指数部分添加进位需要作为独立步骤进行；而根据 L-Mul 中的分段函数 l (m)，如果尾数和大于 2，进位会自动添加到指数。

因此，通过跳过尾数乘法和舍入操作，L-Mul 算法比传统浮点乘法更高效。

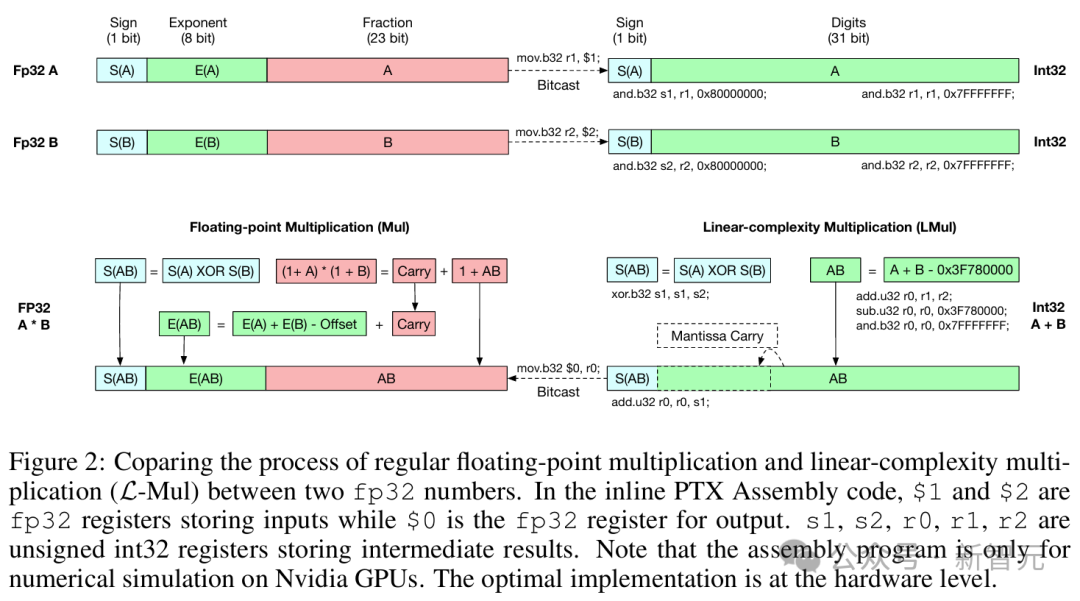
算法的具体实现过程如图 2 所示，最佳实现是在硬件级别，因此作者添加了在英伟达 GPU 上模拟该过程的内联 PTX 汇编代码。
  ~  
  ~  

常规浮点乘法和 L-Mul 算法的复杂度比较；在汇编代码中，$1 和 $2 是存储输入的 fp32 寄存器，$0 是用于输出的 fp32 寄存器。s1、s2、r0、r1、r2 是存储中间结果的无符号 int32 寄存器

L-Mul 结果的构造可以用以下等式表示，其中所有位级计算都作为无符号整数之间的操作执行：
  ~  
  ~  

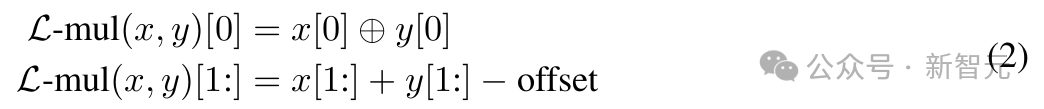在此基础上，作者进一步用 L-Mul 实现了注意力机制。

在 Transformer 模型中，注意力机制由于其处理输入上下文 C 的 O (|C|^2) 复杂度而具有高计算成本。

但如果使用 L-Mul，无需额外训练，就可以用最小的性能损失替代复杂的张量乘法，实现更高效的注意力机制，如下所示：
  ~  
  ~  

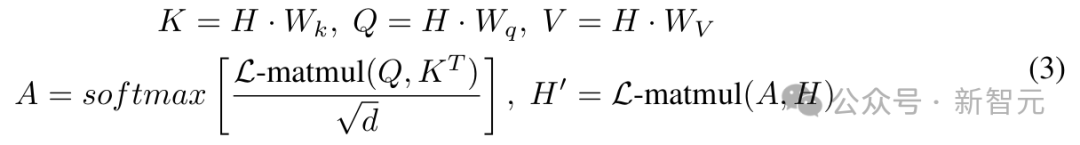其中 L-matmul (Q, K^T) 表示矩阵乘法操作，其中所有常规浮点乘法都被替换为整数加法，用 L-Mul 实现，显著降低了计算资源消耗。

精度和成本分析

精度分析的目标是确定 L-Mul 近似计算的精度，相当于将浮点数的小数部分舍入到多少位，并和具有 2 位或 3 位尾数的 fp8（e5m2 或 e4m3）进行比较。

考虑正浮点数 x、y，并明确舍入后要保留的 k 位，可以写成以下格式：
  ~  
  ~  
  ~  

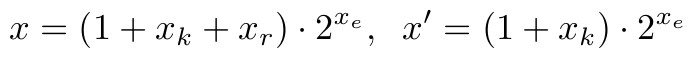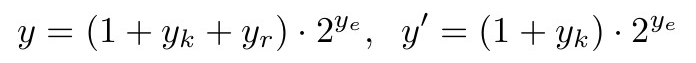其中 x_k、y_k 是 x_m、y_m 的前 k 位，x_r、y_r 是 k 位舍入后将被忽略的剩余位的值。x′、y′是保留尾数前 k 位并进行舍入后的数值。

考虑 x 和 y 在全精度下有 m 位尾数。例如，FP16 有 10 位尾数，BF16 包含 7 位。

乘法运算 Mul (x, y) = x・y 的误差及其期望值可以表示为：
  ~  
  ~  

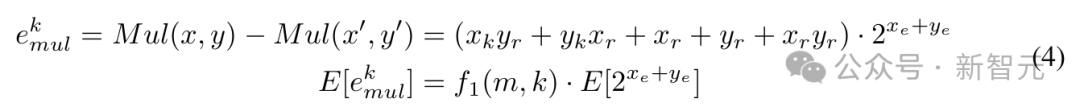与 k 位尾数的浮点乘法相比，k 位尾数 L-Mul 的误差为：

  ~  

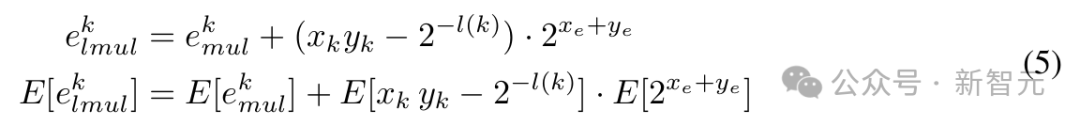利用上述方程，可以计算 k 位 L-Mul 和浮点乘法之间精度差的期望值，具体来说：
  ~  
  ~  

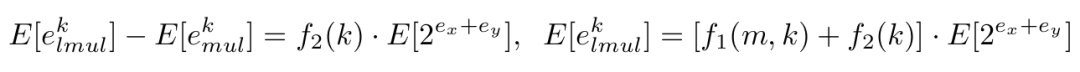当 x_m、y_m 呈均匀分布时，可以计算以下期望：
  ~  
  ~  

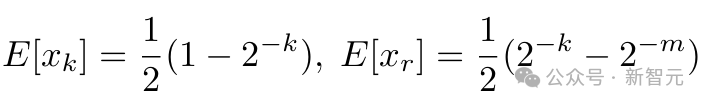通过估计 f1⁢(m,k) 和 f2⁢(k) 并进一步推断 E⁢[e^k_{l⁢m⁢u⁢} k] 和 E⁢[e^k_{m⁢u⁢l}] 可以得知， 如果是在操作数均匀分布的情况下，L-Mul 比 fp8_e5m2 更精确；然而，预训练 LLM 的权重分布通常是存在偏差的。

这种近似计算究竟能否适用于当前的 LLM，还需要实验结果来证明。

基于五个流行大语言模型的组合权重分布，实验结果发现，在实践中，L-Mul 可以在使用 5 位尾数的情况下实现超越 fp8_e4m3 的更高准确度。

此外，结合门运算的复杂度估算可以进一步证实，L-Mul 比 fp8 乘法更加高效且准确。这一结果突显了 L-Mul 在低精度计算中的潜在优势。

关于精度和成本分析的更详细理论推导可见于论文 2.3 节以及附录 A。

LLM 实验结果

要证明 L-Mul 的实际应用价值，就需要在 LLM 的实际任务上运行。

精度分析

论文选择了各种基于 Transformer 的语言模型，包括 Llama 3.1、Mistral、Gemma 2 等，并在各种语言和视觉任务基准上评估了 L-Mul 算法的数值精度。

对比全精度模型权重的运行结果，可以证明，对基于 Transformer 的 LLM 而言，在注意力机制中用 L-Mul 替换标准乘法运算可以达到几乎无损的近似效果，可以在微调或免训练设置下替换 Transformer 层中的不同模块。

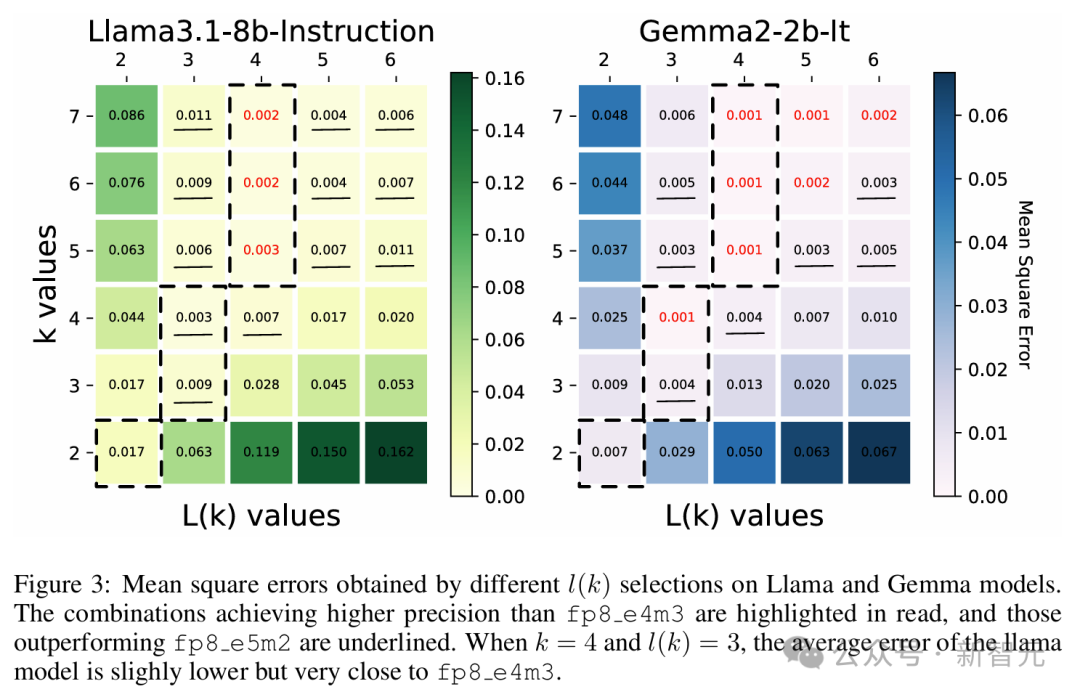
图 3 展示了选择不同 k 值和 l (k) 值的均方误差（mean square errors）结果，实验包含 Llama 3.1 和 Gemma 2 的两个小模型，在 GSM8k 数据集上运行。

在两个模型中，使用 3 位尾数的 L-Mul 比 fp8_e5m2 更精确，而使用 4 位尾数的 L-Mul 可以达到或近似于 fp8_e4m3 的误差水平。
  ~  
  ~  

红色表示平均误差低于 fp8_e4m3，下划线表示误差介于 e4m3 和 e5m2 之间

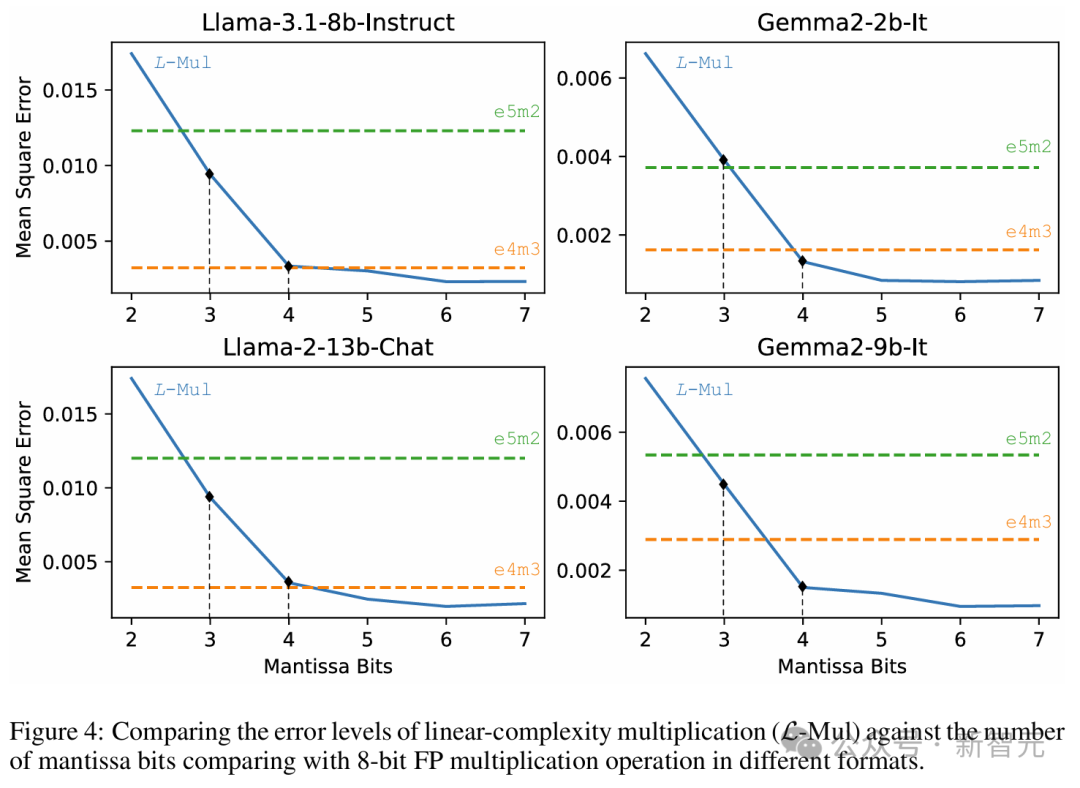
以上两个模型的平均误差如图 4 所示。

前面的理论推导显示，L-Mul 在使用的计算资源少于 fp8_e5m2 时，期望误差可以低于 fp8_e4m3，此处的实验结果正式了前面理论估计的正确性。

实验表明，在各种规模的 LLM 中，使用 6 位尾数 FP 操作数的 L-Mul 算法近似达到最低平均误差，显著优于 e5m2、e4m3 两种 fp8 格式。

此外，3 位和 4 位尾数的 L-Mul 分别达到或超过了 fp8_e5m2 和 fp8_e4m3 的精度。
  ~  
  ~  

L-Mul 与不同格式 fp8 浮点是进行乘法运算的误差水平比较

基准测试

本节的实验旨在证明，L-Mul 可以在不损失性能的情况下替代注意力机制中的张量乘法，而使用 fp8 乘法则会降低推理精度。

这就意味着，L-Mul 可以在降低注意力计算能耗 80% 的同时达到相同的推理性能。

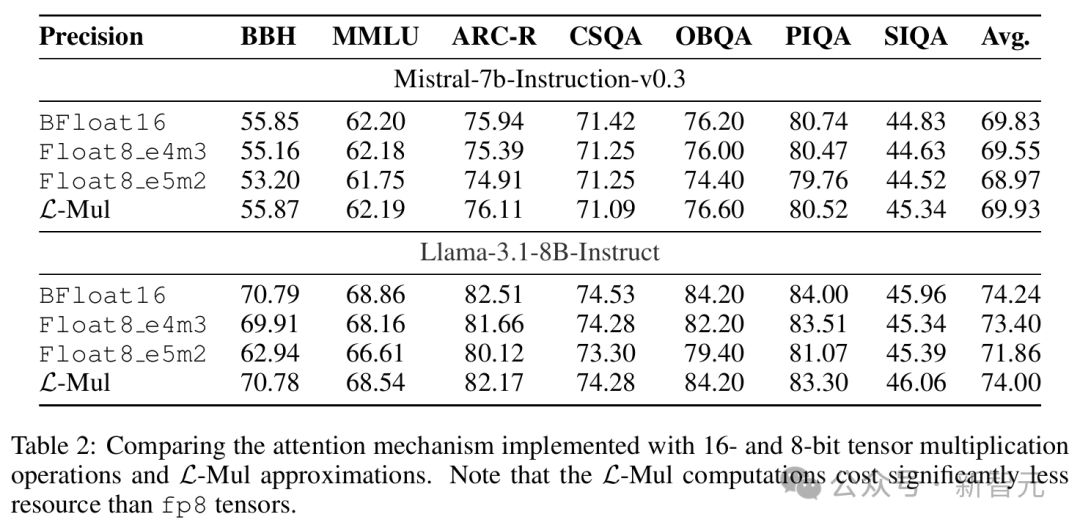
对于文本任务，表 2 展示了 Llama 和 Mistral 模型在各种自然语言基准测试上的评估结果，包括 MMLU、BBH、ARC-C 等。

结果表明，L-Mul 不仅显著减少了计算资源，而且在绝大多数测试中（12/14）的得分高于 fp8_e4m3。

与 bf16 推理相比，性能差距被降低到最低水平。在两个模型中，bf16 和 L-Mul 之间在常识、结构化推理和语言理解方面的平均性能差异仅为 0.07%。
  ~  
  ~  

值得注意的是，对于 Mistral 和 Gemma2 两个模型，基于 L-Mul 的注意力机制与 bf16 基准相比略微提高了平均性能，分别达到 52.92% 和 47.01%。

Llama3.1 使用 L-Mul 时，准确率略低于 bf16，但仍高于 fp8_e4m3 和 fp8_e5m2。

相反，将注意力计算中的张量四舍五入到 fp8_e5m2 会导致显著的性能下降，尽管 e5m2 比 L-Mul 更复杂。
  ~  
  ~  

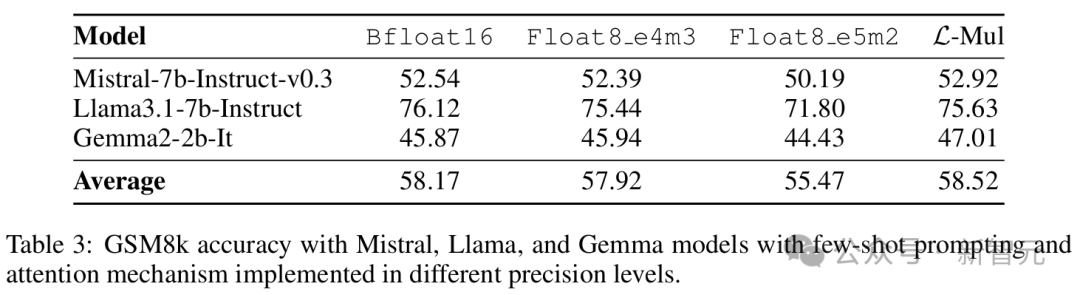
3 个语言模型在 GSM8k 数据集上使用少样本提示的运行结果，包括 L-Mul 方法和 3 种精度 bf16、fp8_e4m3、fp8_e5m2 的对比

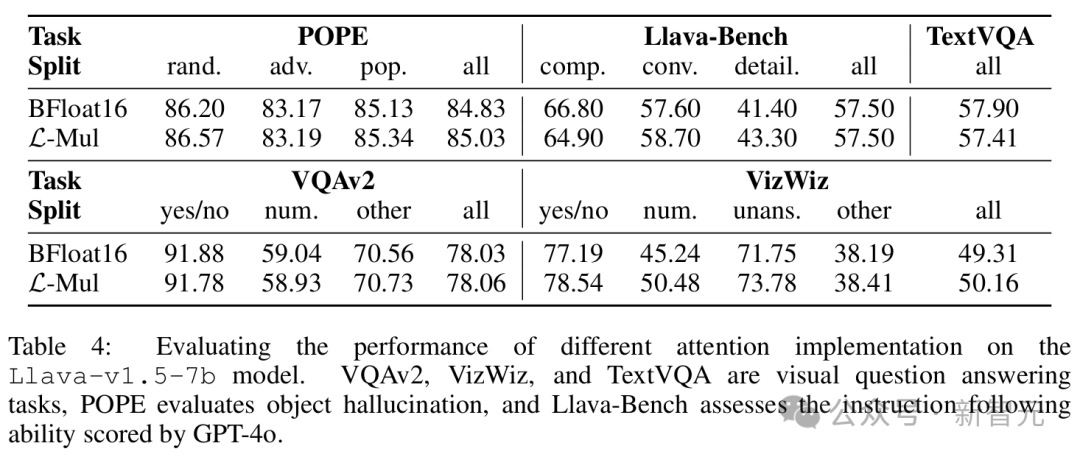
视觉 - 语言任务主要用 Llava 模型进行了测试，结果如表 4 所示。

除了在 TextVQA 基准上的准确率差距略大，达到了 0.5%，在 POPE、VQAv2、Llava-Bench、VizWiz 等其他基准上，L-Mul 达到了和 bf16 相似甚至更好的性能。
  ~  
  ~  

此外，误差估计和消融实验（表 5）可以进一步表明，在无需额外训练的设置下，4 位尾数的 L-Mul 可以达到与 fp8_e4m3 相当的准确性，而 3 位尾数的 L-Mul 优于 fp8_e5m2 乘法。
  ~  
  ~  

微调

以上的实验结果，是直接将预训练 LLM 从标准注意力适配到新的基于 L-Mul 的注意力机制运行的，没有进行额外训练。

进一步的研究还表明，微调可以弥补 L-Mul 和标准乘法之间的性能差距。

本节的实验中，不仅在 Gemma2 的注意力机制层中实现 L-Mul，而且对于模型中所有乘法运算 —— 包括线性变换中的矩阵乘法、元素级乘法以及注意力机制层内的乘法，都使用 L-Mul 和 fp8_e4m3 进行近似，之后在 GSM8k 数据集上对更新后的模型进行微调。

将注意力机制、线性变换和逐元素乘积中的所有乘法运算替换为 3 位尾数 L-Mul 的模型进行微调，其性能可与使用 fp8_e4m3 累积精度的标准模型微调相媲美。

值得注意的是，本实验中的 L-Mul 操作使用 3 位尾数（k=3），累加精度为 fp8_e4m3，以探索极其高效的设置。

结果可以看出，在 fp8 精度下，微调后的 fp8_e4m3 L-Mul 模型达到了与标准微调 fp8_e4m3 模型相当的性能。

这表明，L-Mul 可以在不影响微调模型性能的情况下提高训练效率。此外，也揭示了训练 L-Mul 原生 LLM 的潜质，用于更加精确、节能的模型托管。
  ~  
  ~  

微调后 fp8 和 L-Mul 模型在零样本设置下的评估

作者介绍

Hongyin Luo
  ~  
  ~  

Hongyin Luo 是 MIT 计算机科学与人工智能实验室（CSAIL）的研究科学家，在 Jim Glass 博士领导的口语语言系统（SLS）小组工作。

他于 2016 年在清华大学获得学士学位，导师是 NLP 领域的大牛级人物：刘知远和孙茂松。

随后于 2022 年在 MIT EECS 获得博士学位，专注自然语言处理中的自训练研究。
  ~  
  ~  

他的研究重点是提高语言模型的效率、透明性和推理能力。最新研究结合了自然语言与不同的形式推理引擎，包括蕴涵模型（entailment model）和程序解释器。

他构建了小型语言模型，以 1/500 的计算量表现优于 GPT3-175B，开发了处理搜索引擎噪声的自我去噪语言模型，以及无需任务特定示例即可实现准确推理的自然语言嵌入程序。

参考资料：

• [2410.00907] Addition is All You Need for Energy-efficient Language Models

  https://arxiv.org/abs/2410.00907

• Hongyin Luo 罗鸿胤

  https://luohongyin.github.io/

---

via:

• 【论文日报】LLM 合集：L-Mul 算法 – 在 Transformer 中以整数加法替代乘法，节省高达 95% 算力 AI-PaperDaily 2024 年 10 月 08 日 11:03 北京

  https://mp.weixin.qq.com/s/W7yN-9gVrTOey9FJ8t9s8Q

• 「乘法变加法」！MIT 清华校友全新方法优化 Transformer：Addition is All You Need 新智元 2024 年 10 月 08 日 13:13 北京

  https://mp.weixin.qq.com/s/LdRacBGfjyF8xUJP6h6xbw