【机器学习】LDA线性判别分析

【机器学习】LDA线性判别分析

1. LDA的基本思想

2. LDA求解方法

3. 将LDA推广到多分类

4. LDA算法流程

5. LDA和PCA对比

【附录1】瑞利商与广义瑞利商

        线性判别分析 (Linear Discriminant Analysis，LDA)是一种经典的线性学习方法，在二分类问题上因为最早由[Fisher，1936]提出，亦称"Fisher判别分析"。（严格说来LDA与Fisher判别分析稍有不同，LDA假设了各类样本的协方差矩阵相同且满秩。）

1. LDA的基本思想

        LDA的基本思想是: 给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离，在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。图3.3给出了一个二维示意图。

        

2. LDA求解方法

       问：LDA最终要求什么？

        求投影空间W。 假设要投影到d维空间，W为这最大的d个特征值对应的特征向量张成的矩阵。所以问题转化为求解特征向量w

        求解过程如下：

        给定数据集，，令Xi、цi、∑i分别表示第i∈{0，1}类示例的集合、均值向量、协方差矩阵。

        若将数据投影到直线w上，则两类样本的中心在直线上的投影分别为；若将所有样本点都投影到直线上，则两类样本的协方差分别为。

        由于直线是一维空间，因此。

        本着同类样例的投影点尽可能接近、异类样例的投影点尽可能远离的原则，欲使同类样例的投影点尽可能接近，可以让同类样例投影点的协方差尽可能小，即尽可能小；而欲使异类样例的投影点尽可能远离，可以让类中心之间的距离尽可能大，即尽可能大。同时考虑二者，则可得到欲最大化的目标

        

        定义"类内散度矩阵"

        

        以及"类间散度矩阵"

        

        则式 (3.32)可重写为

         

        这就是LDA欲最大化的目标，即Sw与Sb的"广义瑞利商" （Rayleigh）。根据广义瑞利商的性质，我们知道我们的J(w)最大值为矩阵的最大特征值，而对应的w为的最大特征值对应的特征向量!（具体的瑞利商的知识见【附录1】）

    

    如何求解w呢？（w向量决定投影方向）

        如何确定ω呢? 注意到式(3.35)的分子和分母都是关于ω的二次项，因此式(3.35)的解与ω的长度无关，只与其方向有关。（why? 二次项的性质，若w是一个解，则对于任意常数α，αw也是式(3.35)的解.）

        不失一般性，令，则式(3.35)等价于

         

    由拉格朗日乘子法，上式等价于

        

     其中λ是拉格朗日乘子。注意到的方向恒为，不妨令

        

    代入式 (3.37) 即得

    

 3. 将LDA推广到多分类

        如何将LDA推广到多分类任务中？

        假定存在N个类，且第i类示例数为,我们先定义"全局散度矩阵"

        

        其中μ是所有示例的均值向量。将类内散度矩阵重定义为每个类别的散度矩阵之和，即：

        

        其中，

            

            例如：三类问题如下直观图所示：

                

            显然，多分类 LDA 可以有多种实现方法：使用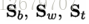 三者中的任何两个即可。

            常见的一种实现是采用优化目标：

            

            其中的tr()为矩阵的迹，一个n×n的对角矩阵A的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵A的迹（或迹数），一般记作tr(A)。