算法之最小生成树(Prim实现)

最小生成树概念：

此处不做详细说明：生成树各边的权值总和称为生成树的权，权最小的生成树称为最小生成树。

---

Prim算法介绍，是一种贪心算法使用邻接矩阵作为存储结构的Prim算法的时间复杂度为O(V*V)，即为本文后续代码的时间复杂度。

如果使用二叉堆与邻接表表示的话，Prim算法的时间复杂度可缩减为O(E log V),其中E为连通图的边数，V为顶点数。如果使用较复杂的斐波那契堆，则可将运行时间进一步缩短为O(E + V log V)，这在连通图足够密集时(边较多，即E满足Ω（V log V）)可较显著地提高运行速度。

以下面这个简单的树为例子介绍代码的实现过程。

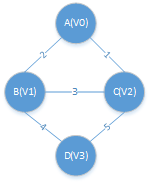
链接矩阵表示法：N代表正无穷，表示两个点无连接

0 , 2 , 1 , N
2 , 0 , 3 , 4
1 , 3 , 0 , 5
N , 4 , 5 , 0

需要辅助参数

int [4] Lowcost  ： 代表已生成的最小树到各结点的最小权值数组

int [4] Adjvex : 代表最小生成树生成的过程 ，依次访问的结点。

---

1、最小生成树从A点开始寻找，初始化变量

Lowcost = {0,2,1,N} 数组里代表A结点到图的各结点（A,B ,C ,D ）的最小权值 

Adjvex[0] = 0 ; 把Ａ点的下标存入数组。

2、循环遍历，需要遍历 4-1 = 3次

第一次遍历：

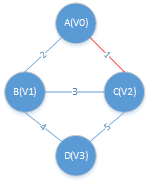
找到与A最小权值最小的结点，对应的边为 A->C,  把C加入到 adjvex[1] = 2;

此时，AC为找到的两树2个结点，接下来更新lowcost，保存结点到(A,B,C,D)到AC这个树的最小距离

lowcost = {0,2,0,5} 

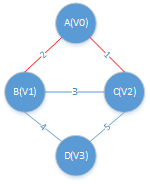
3、第二次遍历：

找到与AC生成树距离最小的结点，对应的边为 A->B,  把B加入到 adjvex[2] = 1;

此时，ACB为找到的两树3个结点，接下来更新lowcost，保存结点到(A,B,C,D)到ACB这个树的最小距离

lowcost = {0,0,0,4} 

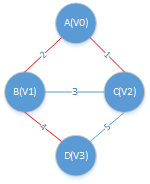
3、第三次遍历：

找到与ACB生成树距离最小的结点，对应的边为 B->D,  把D加入到 adjvex[3] = 3;

此时，ACBD为找到树的4个结点

程序完成，对应的边为  (A->C)(A->B)(B->D)

---

代码如下：代码不是自己写的，改写也了其他博客的代码

public class MinSpanTree {
    public void MinSpanTree_Prim(DigraphMatix di) {

        int adjvex[] = new int[di.verNum]; //存放依次找到的最小生成树的结点
        int lowcost[] = new int[di.verNum];//存放已经生成的最小生成树到所有结点的权重值，已经访问到的结点对应的值为0

        Arrays.fill(adjvex, 0);
        lowcost = Arrays.copyOf(di.getMatrix()[0], di.verNum);
        lowcost[0] = 0;

        for (int i = 1; i < di.verNum; i++) {
            int min = DigraphMatix.INFINITY;

            int j = 0, k = 0;
            //遍历lowcost，找出lowcost中的最小权值，存入min,并记录在数组中的index到变量k。
            while (j < di.verNum) {
                if (lowcost[j] != 0 && lowcost[j] < min) {
                    min = lowcost[j];
                    k = j;
                }
                j++;
            }

            System.out.printf("(%d,%d)", adjvex[k], k);
            lowcost[k] = 0; //把找到的到最小权限结点的权限设置为0 , 此结点后续不会再处理，说明已经遍历过了
            for (int m = 1; m < di.verNum; m++) {
                if (lowcost[m] != 0 && di.getMatrix()[k][m] < lowcost[m]) {
                    lowcost[m] = di.getMatrix()[k][m];
                    adjvex[m] = k;
                }
            }
        }
    }
}

public class DigraphMatix {
    //图矩阵
    int [][] matrix ;
    //权值最大值， 表示正无穷
    public final static  int INFINITY = 25536;
    //树的点个数
    int verNum = 0;

    public DigraphMatix(int[][] di) {
        this.matrix = di;
        verNum = di.length;
    }


    public int[][] getMatrix() {
        return matrix;
    }

    public DigraphMatix(int num) {
        matrix = new int[num][num];
        this.verNum = num;
        for (int i = 0; i < verNum; i++) {
            for (int j = 0; j < verNum; j++) {
                if (j == i) {
                    matrix[i][j] = 0;
                }
                matrix[i][j] = INFINITY;
            }
        }
    }
}