算法之最强连通算法Kosaraju（DFS）实现

最强连通分支

有向图G=(V, E)的一个强连通分支就是一个最大的顶点子集C，对于C中每对顶点(s, t)，有s和t是强连通的，并且t和 s也是强连通的，即顶点s和t是互达的。找出图中给出了强连通的所有分支，有多种算法， 本文介绍Kosaraju算法。

---

算法步骤如下

1、按topSort方法，得到有向图的伪topSort的序列，为什么说是伪？因为topSort是对无回环的图，而现在是对有回环的图进行相同算法得到的结果。但不管图是否有回边，这里就用topSort排序算法，得到一个栈sortTopStack。

2、反置图G, 得到图GT

3、以第一步中的sortTopStack的弹出顺序进行DFS连通树的生成，生成的所有树组成的森林即为最强连通所有分支。

算法时间复杂度为O(V+E)

---

示意图如下：对下面的图进行最大连通算法

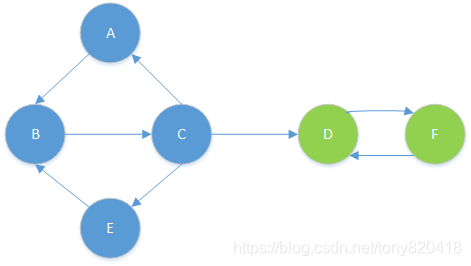
1、按算法第一步执行后，得到sortTopStack，栈的内容

      FDECBA

2、把图进行转置，后结果：

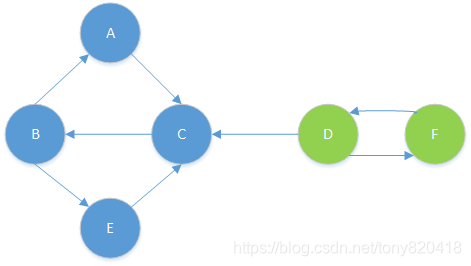
3、按DFS进行连通树的提取，起点顺序按第一步栈中的弹出顺序

    第一步获取的栈为FDECBA ， 获取连通树的顺序为 ABCEDF ,

    如从A开始，连通的点为 ACBE , 则其为一个最强边通分支。

    接着栈中没有最访问到的点为FD,

    从D开始，连通的点为DF , 则其为一个最强分支。

---

再看一个例子

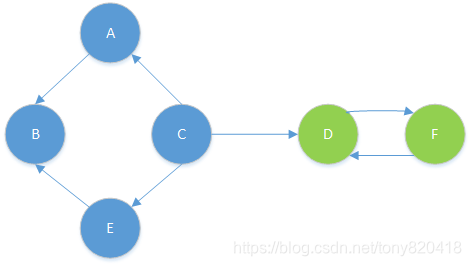
1、topsort排序栈为：  BAFDEC

2、图转置为