《视觉SLAM十四讲》学习笔记：第3讲三维空间刚体运动_四元数和三维欧式空间的外积的关系-优快云博客

本文链接：https://blog.youkuaiyun.com/themarshal/article/details/107370770

《视觉SLAM十四讲》学习笔记：第3讲三维空间刚体运动

前言：本学习笔记将记录《视觉SLAM十四将》中一些重要的知识点，并对书中一些比较难的知识点添加上一些笔者个人的理解，以供笔者本人复习并与各位同学一起交流学习。本笔记结构将与原书结构一致，如果某一目录下面没有任何笔记，则代表笔者认为该小节内容相对来说没有过多重点知识。

本讲主要解决问题
理论：一个刚体在三维空间中的运动如何描述
实践：了解线性代数库Eigen

3.1 旋转矩阵

3.1.1 点、向量和坐标系
1.向量：线性空间的元素，注意只有指定了三维空间中的某个坐标系（或指定了线性空间中的一组基）时，才能够定义该向量在此坐标系下的坐标，如确定了一组基( $\vec{e_1}$ , $\vec{e_2}$ , $\vec{e_3}$ )后，就可以定义向量 $\vec{a}$ 的坐标，如下图所示：
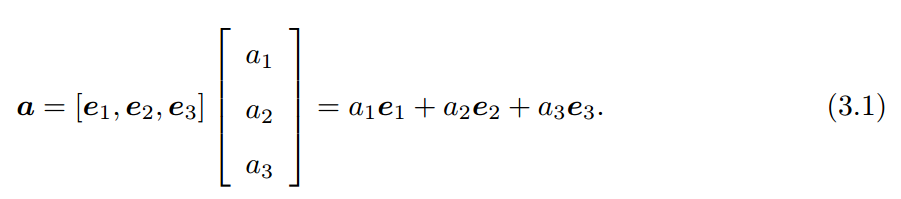
在这里插入图片描述
其中， $a_1$ ， $a_2$ ， $a_3$ 称为向量 $\vec{a}$ 在基( $\vec{e_1}$ , $\vec{e_2}$ , $\vec{e_3}$ )下的坐标。
因此，向量的坐标不仅与向量本身有关，还与我们选取的坐标系有关，不同坐标系下向量的坐标可以通过旋转矩阵获得，此处不过多赘述。
2.向量的内外积：
对于 $\vec{a}，\vec{b} \in R^3$ ，定义内积如下：
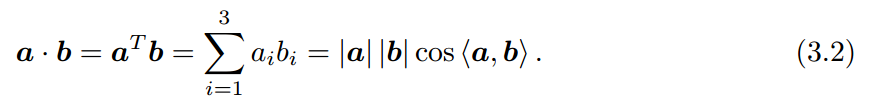
在这里插入图片描述
而定义外积如下：

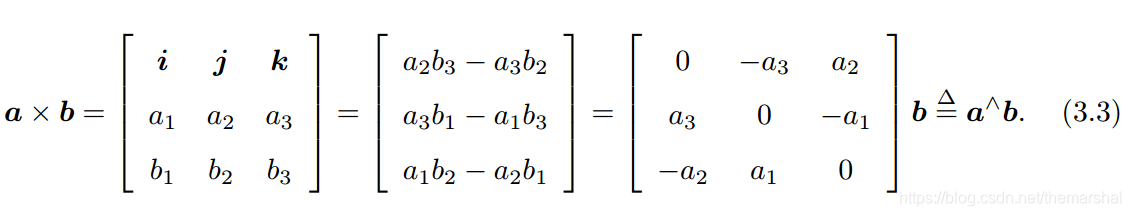
外积的方向垂直于这两个方向，大小等于 $|\vec{a}||\vec{b}|sin\left<\vec{a},\vec{b}\right>$