Leetcode300. 最长递增子序列

最新推荐文章于 2025-05-04 15:46:21 发布

会流泪de鱼

最新推荐文章于 2025-05-04 15:46:21 发布

阅读量172

点赞数

CC 4.0 BY-SA版权

分类专栏： Leetcode 文章标签：算法数据结构 leetcode

本文链接：https://blog.youkuaiyun.com/sunhaiting666/article/details/126354925

Leetcode 专栏收录该内容

214 篇文章

订阅专栏

本文详细解析了LeetCode题目300寻找最长递增子序列的两种方法：动态规划和贪心算法配合二分查找。通过实例代码展示了如何利用dp数组进行状态转移和计算最长递增子序列长度，以及如何利用贪心策略简化问题并提高效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Leetcode300. 最长递增子序列

题目：
给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

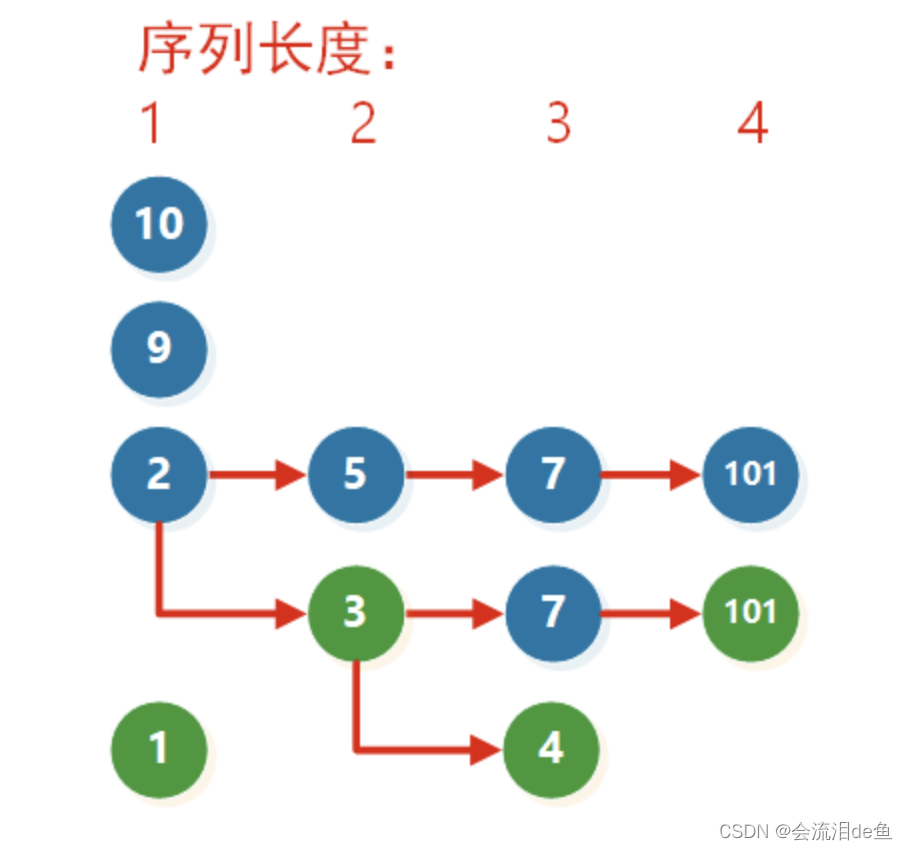
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

题解：
方案一：动态规划
定义 $d p [i]$ 为考虑前 $i$ 个元素，以第 $i$ 个数字结尾的最长上升子序列的长度，注意 $n u m s [i]$ 必须被选取。

我们从小到大计算 $d p$ 数组的值，在计算 $d p [i]$ 之前，我们已经计算出 $d p [0 \dots i - 1]$ 的值，则状态转移方程为：

$d p [i] = ma x (d p [j]) + 1, 其中 0 \leq j < i 且 n u m [j] < n u m [i]$

即考虑往 $d p [0 \dots i - 1]$ 中最长的上升子序列后面再加一个 $n u m s [i]$ 。由于 $d p [j]$ 代表 $n u m s [0 \dots j]$ 中以 $n u m s [j]$ 结尾的最长上升子序列，所以如果能从 $d p [j]$ 这个状态转移过来，那么 $n u m s [i]$ 必然要大于 $n u m s [j]$ ，才能将 $n u m s [i]$ 放在 $n u m s [j]$ 后面以形成更长的上升子序列。

最后，整个数组的最长上升子序列即所有 $d p [i]$ 中的最大值。

$0≤i<n\text{LIS}_{\textit{length}}= \max(\textit{dp}[i]), \text{其中} \, 0\leq i < n$

方案二：贪心+二分法
[10, 9, 2, 5, 3, 7, 101, 4, 1]
在这里插入图片描述

java代码：

 /**
     * 动态规划
     * dp[i]=max(dp[j])+1,其中0≤j<i且num[j]<num[i]
     *
     * @param nums
     * @return
     */
    public static int lengthOfLIS(int[] nums) {
        if (nums == null || nums.length == 0) return 0;
        int len = nums.length;
        int[] dp = new int[len];
        int res = 0;
        for (int i = 1; i < len; i++) {
            dp[i] = 1;
            for (int j = 0; j < i; j++) {
                if (nums[j] < nums[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            res = Math.max(dp[i], res);
        }
        return res;
    }

    /**
     * 贪心+二分法
     *
     * @param nums
     * @return
     */
    public static int lengthOfLIS2(int[] nums) {
        int len = 1;
        int n = nums.length;
        if (n == 0) return 0;
        int[] d = new int[n + 1];
        d[len] = nums[0];

        for (int i = 1; i < n; i++) {
            if (nums[i] > d[len]) {
                len++;
                d[len] = nums[i];
            } else {
                int l = 1, r = len, pos = 0;
                while (l <= r) {
                    int mid = l + (r - l) / 2;
                    if (nums[i] > d[mid]) {
                        pos = mid;
                        l = mid + 1;
                    } else {
                        r = mid - 1;
                    }
                }
                d[pos + 1] = nums[i];
            }
        }
        return len;
    }