Leetcode287. 寻找重复数

原创已于 2022-08-15 17:30:20 修改 · 145 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构

于 2022-08-15 17:28:46 首次发布

Leetcode 专栏收录该内容

214 篇文章

订阅专栏

这篇博客介绍了LeetCode287题的两种解决方案：二分法和双指针法。二分法利用数组元素的单调性找到重复的数；双指针法通过模拟链表环路找到重复的整数。详细阐述了两种方法的思路，并提供了Java代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Leetcode287. 寻找重复数

题目：
给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。
假设 nums 只有一个重复的整数，返回这个重复的数。
你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。

题解：
方案一：二分法
我们定义 $c n t [i]$ 表示 $n u m s$ 数组中小于等于 $i$ 的数有多少个，假设我们重复的数是 $t a r g e t$ ，那么 $[1, t a r g e t - 1]$ 里的所有数满足 $c n t [i] \leq i$ ， $[t a r g e t, n]$ 里的所有数满足 $c n t [i] > i$ ，具有单调性。

以示例 1 为例，我们列出每个数字的 $c n t$ 值：

nums	1	2	3	4
cnt	1	3	4	5

示例中重复的整数是 2，我们可以看到 $[1, 1]$ 中的数满足 $c n t [i] \leq i$ ， $[2, 4]$ 中的数满足 $c n t [i] > i$ 。

如果知道 $c n t []$ 数组随数字 $i$ 逐渐增大具有单调性（即 $t a r g e t$ 前 $c n t [i] \leq i$ ， $t a r g e t$ 后 $c n t [i] > i$ ），那么我们就可以直接利用二分查找来找到重复的数。

但这个性质一定是正确的吗？考虑 $n u m s$ 数组一共有 $n + 1$ 个位置，我们填入的数字都在 $[1, n]$ 间，有且只有一个数重复放了两次以上。对于所有测试用例，考虑以下两种情况：

如果测试用例的数组中 $t a r g e t$ 出现了两次，其余的数各出现了一次，这个时候肯定满足上文提及的性质，因为小于 $t a r g e t$ 的数 $i$ 满足 $c n t [i] = i$ ，大于等于 $t a r g e t$ 的数 $j$ 满足 $c n t [j] = j + 1$ 。
如果测试用例的数组中 $t a r g e t$ 出现了三次及以上，那么必然有一些数不在 $n u m s$ 数组中了，这个时候相当于我们用 $t a r g e t$ 去替换了这些数，我们考虑替换的时候对 $c n t []$ 数组的影响。如果替换的数 $i$ 小于
$t a r g e t$ ，那么 $[i, t a r g e t - 1]$ 的 $c n t$ 值均减一，其他不变，满足条件。如果替换的数 $j$ 大于等于
$t a r g e t$ ，那么 $[t a r g e t, j - 1]$ 的 $c n t$ 值均加一，其他不变，亦满足条件。

方案二：双指针
使用环形链表II的方法解题（142环形链表II），使用 142 题的思想来解决此题的关键是要理解如何将输入的数组看作为链表。
首先明确前提，整数的数组 nums 中的数字范围是 [1,n]。考虑一下两种情况：

如果数组中没有重复的数，以数组 [1,3,4,2]为例，我们将数组下标 n 和数 $n u m s [n]$ 建立一个映射关系 $f (n)$ ，
其映射关系 $n - > f (n)$ 为：
0->1
1->3
2->4
3->2
我们从下标为 0 出发，根据 $f (n)$ 计算出一个值，以这个值为新的下标，再用这个函数计算，以此类推，直到下标超界。这样可以产生一个类似链表一样的序列。
0->1->3->2->4->null

如果数组中有重复的数，以数组 [1,3,4,2,2] 为例,我们将数组下标 n 和数 $n u m s [n]$ 建立一个映射关系 $f (n)$ ，
其映射关系 $n - > f (n)$ 为：
0->1
1->3
2->4
3->2
4->2
同样的，我们从下标为 0 出发，根据 $f (n)$ 计算出一个值，以这个值为新的下标，再用这个函数计算，以此类推产生一个类似链表一样的序列。
0->1->3->2->4->2->4->2->……
这里 2->4 是一个循环，那么这个链表可以抽象为下图：
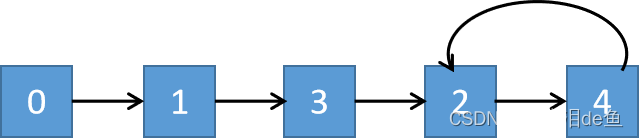
在这里插入图片描述

从理论上讲，数组中如果有重复的数，那么就会产生多对一的映射，这样，形成的链表就一定会有环路了，

综上
1.数组中有一个重复的整数 <> 链表中存在环
2.找到数组中的重复整数 <> 找到链表的环入口

至此，问题转换为 142 题。那么针对此题，快、慢指针该如何走呢。根据上述数组转链表的映射关系，可推出
142 题中慢指针走一步 slow = slow.next ==> 本题 slow = nums[slow]
142 题中快指针走两步 fast = fast.next.next ==> 本题 fast = nums[nums[fast]]

java代码：

 /**
     * 二分法
     *
     * @param nums
     * @return
     */
    public static int findDuplicate(int[] nums) {
        int len = nums.length;
        int left = 1, right = len - 1;
        int res = -1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            int cnt = 0;
            for (int i = 0; i < len; i++) {
                if (nums[i] <= mid) {
                    cnt++;
                }
            }
            if (cnt <= mid) {
                left = mid + 1;
            } else {
                right = mid - 1;
                res = mid;
            }
        }
        return res;
    }


    /**
     * 双指针
     *
     * @param nums
     * @return
     */
    public static int findDuplicate2(int[] nums) {
        int fast = 0;
        int slow = 0;

        slow = nums[slow];
        fast = nums[nums[fast]];
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[nums[fast]];
        }

        int pre1 = 0;
        int pre2 = slow;
        while (pre1 != pre2) {
            pre1 = nums[pre1];
            pre2 = nums[pre2];
        }
        return pre1;
    }