#单调队列，动态规划，斜率优化#hdu 3507 Print Article

最新推荐文章于 2025-04-11 09:14:47 发布

lemondinosaur

最新推荐文章于 2025-04-11 09:14:47 发布

阅读量224

点赞数

CC 4.0 BY-SA版权

分类专栏：线性dp 单调队列、斜率优化文章标签： hdu 3507 Print Article

本文链接：https://blog.youkuaiyun.com/sugar_free_mint/article/details/81783534

线性dp 同时被 2 个专栏收录

99 篇文章

订阅专栏

单调队列、斜率优化

30 篇文章

订阅专栏

本文介绍了一种使用动态规划解决打印文章最小花费的方法，并通过优化算法的时间复杂度来提高效率。文中详细分析了如何利用单调队列维护下凸壳来避免不必要的计算，从而将时间复杂度从O(n^2)降低到更高效的级别。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

一篇文章在打印k个需花费
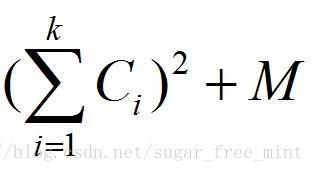
这里写图片描述
m是常数，问最少花费多少就可以打完一篇文章

分析

对于 $x 1 < x$ and $x 2 < x$
可得 $dp[x]=dp[x1]+(sum[x]-sum[x1-1])^2+m$
$dp[x]=dp[x2]+(sum[x]-sum[x2-1])^2+m$
但是 $O(n^2)$ 会超时
设 $x 1 < x 2$ and $d p (x 1) < d p (x 2)$
变形可得
$dp[x2]+sum[x2−1]2−dp[x1]−sum[x1−1]22(sum[x2−1]−sum[x1−1])<sum[x]\dfrac{dp[x2]+sum[x2-1]^2-dp[x1]-sum[x1-1]^2}{2(sum[x2-1]-sum[x1-1])}<sum[x]$
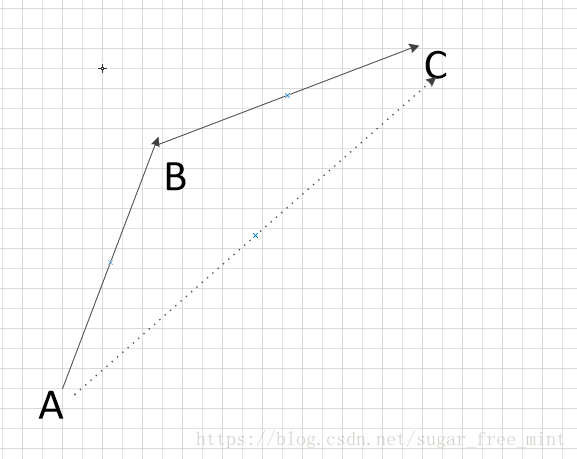
这里写图片描述
所以如果ANSWER(BC)<=sum[x],证明B点劣于C点，可以去掉B点。否则ANSWER(BC)>sum[x],如果ANSWER(AB)>=ANSWER(BC),则有ANSWER(AB)>sum[x],证明A点优于B点，可去掉B点。所以单调队列维护下凸壳

代码

#include <cstdio>
using namespace std;
typedef unsigned long long ull;
int n,m,q[500001],head,tail; ull sum[500001],f[500001];
ull in(){
	ull ans=0; char c=getchar();
	while (c<48||c>57) c=getchar();
	while (c>47&&c<58) ans=ans*10+c-48,c=getchar();
	return ans;
}
ull print(ull ans){if (ans>9) print(ans/10); putchar(ans%10+48);}
ull up(int i,int j){return f[i]+sum[i]*sum[i]-f[j]-sum[j]*sum[j];}//分子
ull down(int i,int j){return (sum[i]-sum[j])<<1;}//分母
ull dp(int i,int j){return f[j]+(sum[i]-sum[j])*(sum[i]-sum[j])+m;}//dp的答案
int main(){
	while (scanf("%d%d",&n,&m)==2){
		f[0]=q[head=tail=1]=0;
		for (register int i=1;i<=n;i++){
			sum[i]=sum[i-1]+in();
			while (head<tail&&up(q[head+1],q[head])<=sum[i]*down(q[head+1],q[head])) head++;
			f[i]=dp(i,q[head]);
			while (head<tail&&up(i,q[tail])*down(q[tail],q[tail-1])<=up(q[tail],q[tail-1])*down(i,q[tail])) tail--;//答案更优
		    q[++tail]=i;
		} 
		print(f[n]); putchar('\n');
	}
	return 0;
}