基于ACO蚁群优化算法的多车辆含时间窗VRPTW问题求解matlab仿真

最新推荐文章于 2025-12-13 19:26:52 发布

原创最新推荐文章于 2025-12-13 19:26:52 发布 · 708 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #matlab #ACO #蚁群优化 #多车辆 #时间窗 #VRPTW

MATLAB程序开发同时被 3 个专栏收录

228 篇文章

订阅专栏

优化

81 篇文章

订阅专栏

路线规划

32 篇文章

订阅专栏

1.程序功能描述

带时间窗的多车辆路径规划问题(Vehicle Routing Problem with Time Windows, VRPTW)是 VRP的重要扩展，其要求配送车辆在客户指定的时间窗内完成服务，同时需满足车辆容量、行驶成本等约束条件。蚁群优化算法是一种模拟自然界蚂蚁觅食行为的启发式智能优化算法，具有分布式计算、正反馈机制和较强鲁棒性等特点，非常适合求解VRPTW这类NP-hard组合优化问题。

2.测试软件版本以及运行结果展示

MATLAB2022A/MATLAB2024B版本运行

3.部分程序

.......................................................................
    %四：更新信息素矩阵（基于当前最优路径）
    bestR                   = Route_best(jk,:); 
    % 解码最优路径，得到有效车辆路径、车辆数、总距离
    [~,Ncar_best,Lall_best] = func_decode(bestR,Cap,demands,T1start,T1end,Tends,Tser,dist);
    % 调用函数更新信息素（挥发旧信息素+新增最优路径的信息素）
    Tau                     = func_newTau(Tau,bestR,rho,Q,Cap,demands,T1start,T1end,Tends,Tser,dist);
    
    %五：打印当前迭代的最优解信息
    disp(['车辆数：',num2str(Ncar_best),'，总距离：',num2str(Lall_best)]);
    fprintf('\n')  % 换行，优化输出格式
    % 清空路径表，为下一代蚂蚁路径构建做准备  
    Table=zeros(Xnum,cusnum);  
    dists(jk)=Lall_best;  % 记录当前代最优总距离（注：dists未提前定义，建议先初始化）
    Ncars(jk)=Ncar_best;  % 记录当前代最优车辆数（注：Ncars未提前定义，建议先初始化）

%解码最优路径，得到有效车辆路径、车辆数、总距离
[bestVC,NV,TD]=func_decode(Route_best(end,:),Cap,demands,T1start,T1end,Tends,Tser,dist);
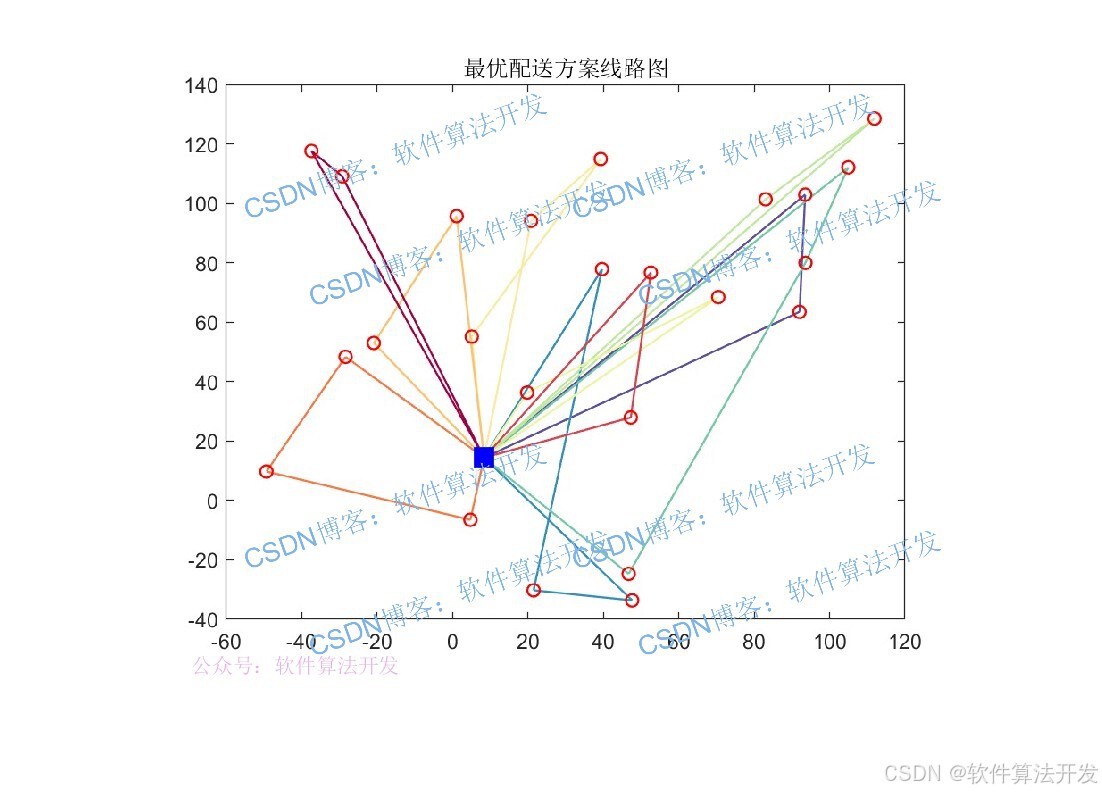
func_draw(bestVC,Posxy);  


figure  
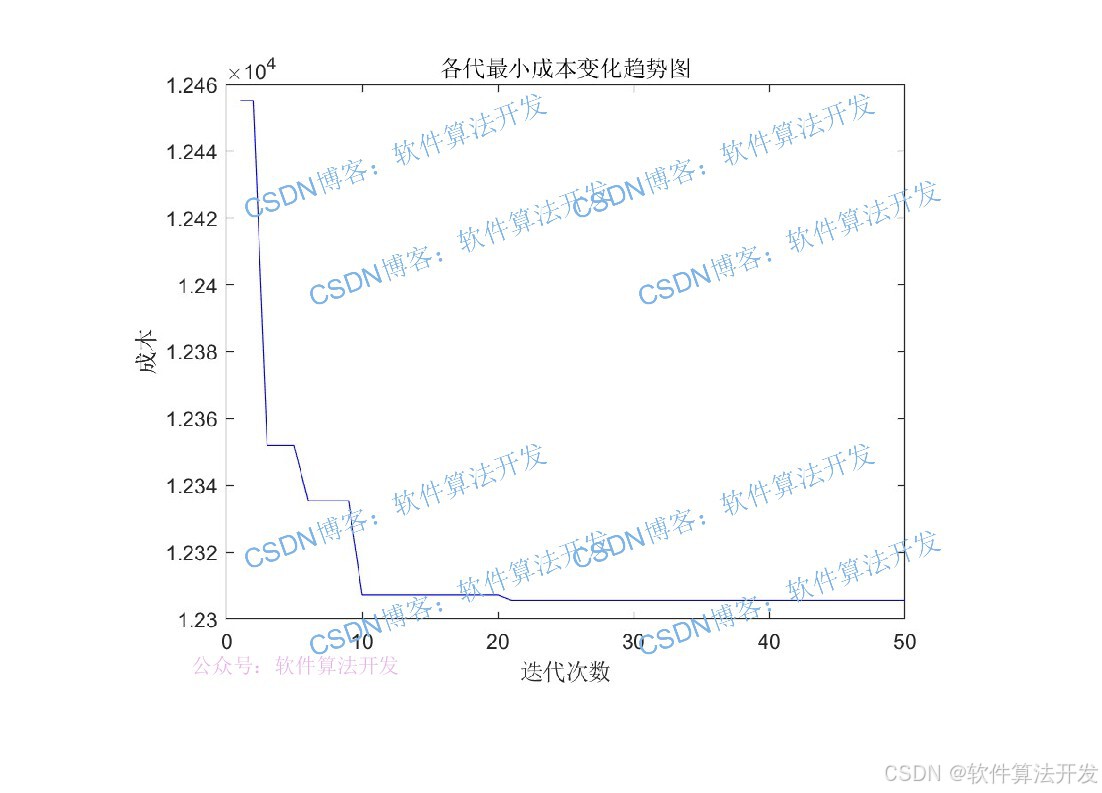
plot(1:iter_max,Cost_best,'b')   
xlabel('迭代次数')   
ylabel('成本')       
title('各代最小成本变化趋势图')   
125

4.算法理论概述

VRPTW可描述为：存在一个配送中心和n个客户点，每个客户点有确定的需求量qi、服务时间窗[ai,bi](ai为最早服务时间,bi为最晚服务时间)和服务时长si,现有m辆配送车辆，每辆车的最大容量为 Q，车辆从配送中心出发，完成客户服务后需返回配送中心；目标是规划最优的车辆行驶路径，满足所有约束条件，并使总行驶成本(或总行驶距离、总时间)最小。

目标函数（以最小化总行驶成本为例）：

蚁群优化算法由意大利学者于1992年提出，其灵感来源于自然界中蚂蚁的觅食行为：蚂蚁在行走过程中会分泌一种称为信息素（Pheromone）的化学物质，信息素会随着时间挥发；后续蚂蚁会倾向于选择信息素浓度高的路径，而路径上的信息素浓度又会因蚂蚁的选择而增强——这一正反馈机制最终会引导整个蚁群找到从蚁巢到食物源的最短路径。

其实现步骤如下：

步骤1：算法参数初始化

输入客户点数量n、车辆数量m、车辆最大容量Q、各客户点的需求量qi、时间窗[ai,bi]、服务时长si、节点间的距离dij、行驶时间tij和行驶成本cij 。

步骤2：蚂蚁构建可行路径

每只蚂蚁从配送中心出发，按照状态转移规则依次选择下一个客户点，同时满足容量约束和时间窗约束，直到所有客户点都被服务，最后返回配送中心。