基于海鸥优化的LSTM深度学习网络模型(SOA-LSTM)的一维时间序列预测算法matlab仿真

目录

1.程序功能描述

2.测试软件版本以及运行结果展示

3.部分程序

4.算法理论概述

5.完整程序

---

1.程序功能描述

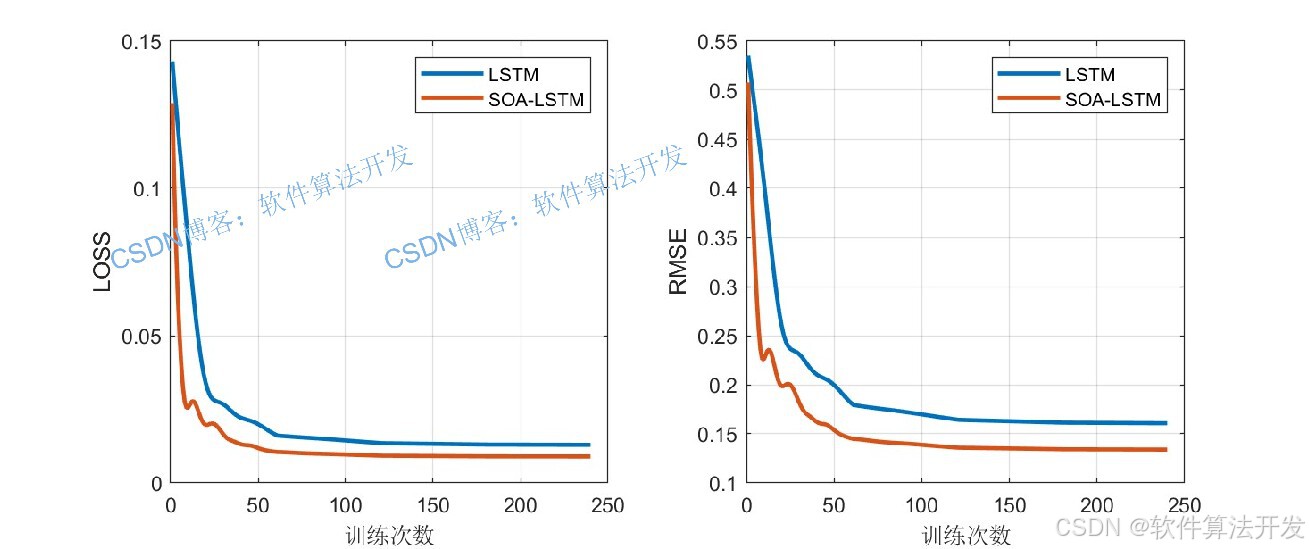
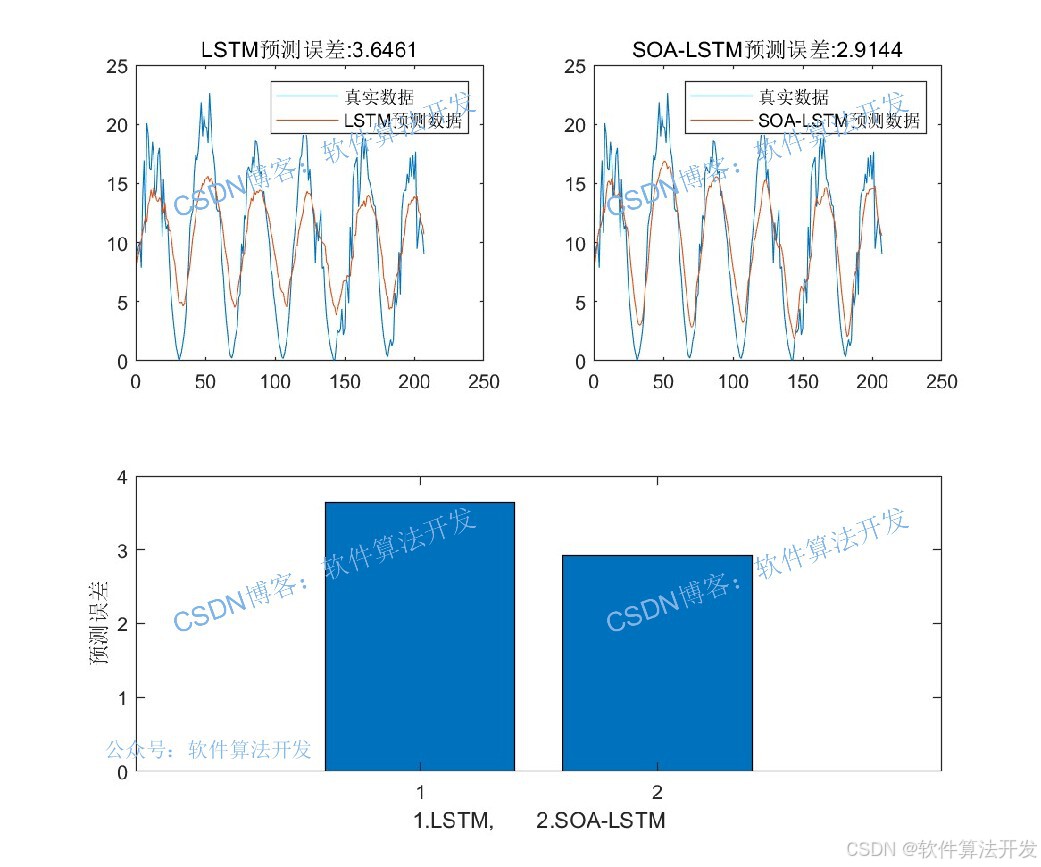
       传统LSTM网络用于时间序列预测时，初始权重、学习率等超参数常依赖人工调试，易导致模型收敛慢、预测精度低。海鸥优化算法（SOA）模拟海鸥捕食与迁徙的智能行为，具备全局寻优能力。SOA-LSTM模型通过SOA优化LSTM关键超参数，结合LSTM对时序数据的长短期依赖捕捉能力，提升一维时间序列的预测性能。

2.测试软件版本以及运行结果展示

MATLAB2022A/MATLAB2024B版本运行

3.部分程序

   %更新位置
   for j=1:Npop
    fitness_new(j) = fobj(X_new(j,:));
   end
   for j = 1:Npop
    if(fitness_new(j) < GBestF)
        GBestF = fitness_new(j);
        GBestX = X_new(j,:);   
    end
   end
    X = X_new;
    fitness = fitness_new;
    %排序更新
   [fitness, index]= sort(fitness);%排序
   for j = 1:Npop
      X(j,:) = X(index(j),:);
   end
   curve(t) = GBestF;

% 将优化得到的最佳参数转换为整数，作为LSTM隐藏层神经元数量
NN=floor(Best_pos)+1;

% 定义LSTM神经网络结构
.....................................
% 训练LSTM网络
[net,INFO] = trainNetwork(Pxtrain, Txtrain, layers, options);

% 使用训练好的网络进行预测
Dat_yc1  = predict(net, Pxtrain);  % 对训练数据进行预测
Dat_yc2  = predict(net, Pxtest);   % 对测试数据进行预测
 
% 将预测结果反归一化，恢复原始数据范围
Datn_yc1 = mapminmax('reverse', Dat_yc1, Norm_O); 
Datn_yc2 = mapminmax('reverse', Dat_yc2, Norm_O); 

% 将细胞数组转换为矩阵
Datn_yc1 = cell2mat(Datn_yc1);
Datn_yc2 = cell2mat(Datn_yc2);

% 保存训练信息、预测结果和收敛曲线
save R2.mat INFO Datn_yc1 Datn_yc2 T_train T_test curve

4.算法理论概述

        LSTM通过 “门控机制” 解决传统循环神经网络（RNN）的梯度消失 / 爆炸问题，其核心结构包括输入门（Input Gate）、遗忘门（Forget Gate）、细胞状态（Cell State）和输出门（Output Gate）。设LSTM网络层N的取值，N∈[N_min, N_max]，如 N_min=10、N_max=50）。 以LSTM在训练集上的预测误差作为适应度函数，采用均方根误差，公式为：

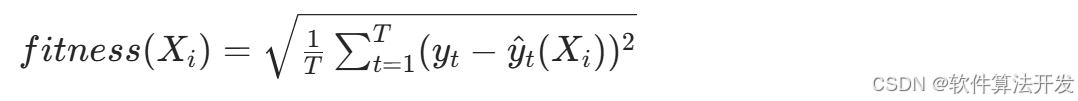
其中，T为训练集样本数， yt为t时刻真实值， y^ t ​ (Xi ​) 为基于个体 Xi的LSTM预测值。

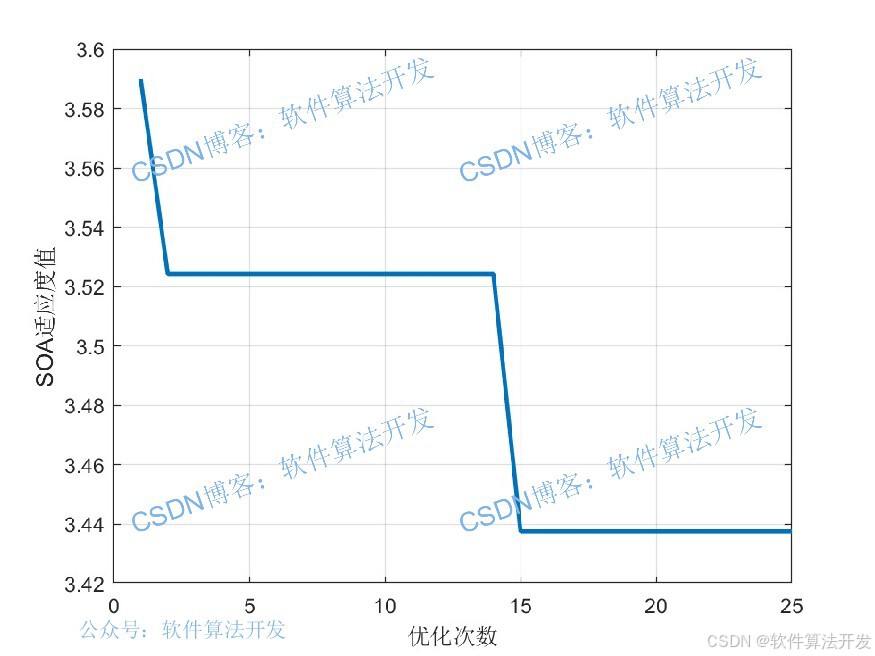
SOA-LSTM以“LSTM预测误差最小”为目标，通过SOA优化LSTM的关键超参数（如隐藏层神经元数n），流程为：​

1.SOA 初始化种群（每个个体对应一组LSTM超参数）；​

2.每组超参数构建LSTM模型，训练后计算预测误差（如MSE）作为SOA适应度值；​

3.SOA通过迁徙-聚集-捕食迭代更新种群，筛选最优超参数；​

4.用最优超参数构建LSTM，完成时间序列预测。

       SOA-LSTM相比传统LSTM，无需人工反复调试超参数，通过SOA的全局寻优能力找到更优超参数组合，在一维时间序列预测中表现出收敛更快、预测精度更高、鲁棒性更强的特点。

5.完整程序

VVV