1.3
练习题
1.
对 Rn\mathbb{R}^nRn 中的任意向量 u\mathbf{u}u 与 v\mathbf{v}v,证明 u+v=v+u\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}u+v=v+u。
证明过程:
设 u=(u1,u2,…,un)\mathbf{u} = (u_1, u_2, \dots, u_n)u=(u1,u2,…,un),v=(v1,v2,…,vn)\mathbf{v} = (v_1, v_2, \dots, v_n)v=(v1,v2,…,vn) 为 Rn\mathbb{R}^nRn 中的任意向量。
根据向量加法的定义:
u+v=(u1+v1,u2+v2,…,un+vn)
\mathbf{u} + \mathbf{v} = (u_1 + v_1, u_2 + v_2, \dots, u_n + v_n)
u+v=(u1+v1,u2+v2,…,un+vn)
由实数加法的交换律:
=(v1+u1,v2+u2,…,vn+un)
= (v_1 + u_1, v_2 + u_2, \dots, v_n + u_n)
=(v1+u1,v2+u2,…,vn+un)
再次应用向量加法的定义:
=v+u
= \mathbf{v} + \mathbf{u}
=v+u
结论:
对 Rn\mathbb{R}^nRn 中的任意向量 u\mathbf{u}u 与 v\mathbf{v}v,均有 u+v=v+u\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}u+v=v+u。
2.
hhh 取什么值时,向量 y\mathbf{y}y 属于 Span{v1,v2,v3}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3\}Span{v1,v2,v3}?
其中:
v1=[1−1−2], v2=[5−4−7], v3=[−310], y=[−43h] \mathbf{v}_1 = \begin{bmatrix} 1 \\ -1 \\ -2 \end{bmatrix},\ \mathbf{v}_2 = \begin{bmatrix} 5 \\ -4 \\ -7 \end{bmatrix},\ \mathbf{v}_3 = \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix},\ \mathbf{y} = \begin{bmatrix} -4 \\ 3 \\ h \end{bmatrix} v1=1−1−2, v2=5−4−7, v3=−310, y=−43h
解题思路:
y∈Span{v1,v2,v3}\mathbf{y} \in \text{Span}\{\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3\}y∈Span{v1,v2,v3} 当且仅当存在标量 x1,x2,x3x_1, x_2, x_3x1,x2,x3 使得:
x1v1+x2v2+x3v3=y
x_1\mathbf{v}_1 + x_2\mathbf{v}_2 + x_3\mathbf{v}_3 = \mathbf{y}
x1v1+x2v2+x3v3=y
增广矩阵:
[15−3−4−1−413−2−70h]
\begin{bmatrix}
1 & 5 & -3 & -4 \\
-1 & -4 & 1 & 3 \\
-2 & -7 & 0 & h
\end{bmatrix}
1−1−25−4−7−310−43h
行变换过程:
-
将第二行替换为 R2+R1R_2 + R_1R2+R1,将第三行替换为 R3+2R1R_3 + 2R_1R3+2R1:
[15−3−401−2−103-6h-8] \begin{bmatrix} 1 & 5 & -3 & -4 \\ 0 & 1 & -2 & -1 \\ 0 & \text{3} & \text{-6} & \text{h-8} \end{bmatrix} 100513−3−2-6−4−1h-8
注:R3+2R1=[−2+2(1), −7+2(5), 0+2(−3), h+2(−4)]=[0,3,−6,h−8]R_3 + 2R_1 = [-2+2(1),\ -7+2(5),\ 0+2(-3),\ h+2(-4)] = [0, 3, -6, h-8]R3+2R1=[−2+2(1), −7+2(5), 0+2(−3), h+2(−4)]=[0,3,−6,h−8] -
将第三行替换为 R3−3R2R_3 - 3R_2R3−3R2:
[15−3−401−2−1000h-5] \begin{bmatrix} 1 & 5 & -3 & -4 \\ 0 & 1 & -2 & -1 \\ 0 & 0 & 0 & \text{h-5} \end{bmatrix} 100510−3−20−4−1h-5
相容性条件:
- 第三行对应方程 0x1+0x2+0x3=h−50x_1 + 0x_2 + 0x_3 = h-50x1+0x2+0x3=h−5。
- 为使方程组相容,需 h−5=0h-5 = 0h−5=0,即 h=5h = 5h=5。
- 此时第三行为 [0 0 0 0][0\ 0\ 0\ 0][0 0 0 0],方程组有解。
结论:
当且仅当 h=5h = 5h=5 时,向量 y\mathbf{y}y 属于 Span{v1,v2,v3}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3\}Span{v1,v2,v3}。
3.
假设 w1,w2,w3,u\mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3, \mathbf{u}w1,w2,w3,u 和 v∈Rn\mathbf{v} \in \mathbb{R}^nv∈Rn,并且 u,v∈Span{w1,w2,w3}\mathbf{u}, \mathbf{v} \in \text{Span}\{\mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3\}u,v∈Span{w1,w2,w3}。证明 u+v∈Span{w1,w2,w3}\mathbf{u} + \mathbf{v} \in \text{Span}\{\mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3\}u+v∈Span{w1,w2,w3}。
证明过程:
-
由 u∈Span{w1,w2,w3}\mathbf{u} \in \text{Span}\{\mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3\}u∈Span{w1,w2,w3},存在标量 c1,c2,c3c_1, c_2, c_3c1,c2,c3 使得:
u=c1w1+c2w2+c3w3 \mathbf{u} = c_1\mathbf{w}_1 + c_2\mathbf{w}_2 + c_3\mathbf{w}_3 u=c1w1+c2w2+c3w3 -
由 v∈Span{w1,w2,w3}\mathbf{v} \in \text{Span}\{\mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3\}v∈Span{w1,w2,w3},存在标量 d1,d2,d3d_1, d_2, d_3d1,d2,d3 使得:
v=d1w1+d2w2+d3w3 \mathbf{v} = d_1\mathbf{w}_1 + d_2\mathbf{w}_2 + d_3\mathbf{w}_3 v=d1w1+d2w2+d3w3 -
将两式相加:
u+v=(c1+d1)w1+(c2+d2)w2+(c3+d3)w3 \mathbf{u} + \mathbf{v} = (c_1 + d_1)\mathbf{w}_1 + (c_2 + d_2)\mathbf{w}_2 + (c_3 + d_3)\mathbf{w}_3 u+v=(c1+d1)w1+(c2+d2)w2+(c3+d3)w3 -
令 e1=c1+d1e_1 = c_1 + d_1e1=c1+d1,e2=c2+d2e_2 = c_2 + d_2e2=c2+d2,e3=c3+d3e_3 = c_3 + d_3e3=c3+d3,则:
u+v=e1w1+e2w2+e3w3 \mathbf{u} + \mathbf{v} = e_1\mathbf{w}_1 + e_2\mathbf{w}_2 + e_3\mathbf{w}_3 u+v=e1w1+e2w2+e3w3
其中 e1,e2,e3e_1, e_2, e_3e1,e2,e3 仍为标量。
结论:
u+v∈Span{w1,w2,w3}\mathbf{u} + \mathbf{v} \in \text{Span}\{\mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3\}u+v∈Span{w1,w2,w3}。
这证明了 Span{w1,w2,w3}\text{Span}\{\mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3\}Span{w1,w2,w3} 在向量加法下是封闭的。
习题 1.3
1.
计算 u+v\mathbf{u} + \mathbf{v}u+v 与 u−2v\mathbf{u} - 2\mathbf{v}u−2v:
u=[−12], v=[−3−1] \mathbf{u} = \begin{bmatrix} -1 \\ 2 \end{bmatrix},\ \mathbf{v} = \begin{bmatrix} -3 \\ -1 \end{bmatrix} u=[−12], v=[−3−1]
计算过程:
- u+v=[−12]+[−3−1]=[−1+(−3)2+(−1)]=[−41]\mathbf{u} + \mathbf{v} = \begin{bmatrix} -1 \\ 2 \end{bmatrix} + \begin{bmatrix} -3 \\ -1 \end{bmatrix} = \begin{bmatrix} -1+(-3) \\ 2+(-1) \end{bmatrix} = \begin{bmatrix} -4 \\ 1 \end{bmatrix}u+v=[−12]+[−3−1]=[−1+(−3)2+(−1)]=[−41]
- u−2v=[−12]−2[−3−1]=[−12]+[62]=[54]\mathbf{u} - 2\mathbf{v} = \begin{bmatrix} -1 \\ 2 \end{bmatrix} - 2\begin{bmatrix} -3 \\ -1 \end{bmatrix} = \begin{bmatrix} -1 \\ 2 \end{bmatrix} + \begin{bmatrix} 6 \\ 2 \end{bmatrix} = \begin{bmatrix} 5 \\ 4 \end{bmatrix}u−2v=[−12]−2[−3−1]=[−12]+[62]=[54]
结论:
u+v=[−41],u−2v=[54]
\mathbf{u} + \mathbf{v} = \begin{bmatrix} -4 \\ 1 \end{bmatrix},\quad
\mathbf{u} - 2\mathbf{v} = \begin{bmatrix} 5 \\ 4 \end{bmatrix}
u+v=[−41],u−2v=[54]
2.
计算 u+v\mathbf{u} + \mathbf{v}u+v 与 u−2v\mathbf{u} - 2\mathbf{v}u−2v:
u=[32], v=[2−1] \mathbf{u} = \begin{bmatrix} 3 \\ 2 \end{bmatrix},\ \mathbf{v} = \begin{bmatrix} 2 \\ -1 \end{bmatrix} u=[32], v=[2−1]
计算过程:
- u+v=[32]+[2−1]=[3+22+(−1)]=[51]\mathbf{u} + \mathbf{v} = \begin{bmatrix} 3 \\ 2 \end{bmatrix} + \begin{bmatrix} 2 \\ -1 \end{bmatrix} = \begin{bmatrix} 3+2 \\ 2+(-1) \end{bmatrix} = \begin{bmatrix} 5 \\ 1 \end{bmatrix}u+v=[32]+[2−1]=[3+22+(−1)]=[51]
- u−2v=[32]−2[2−1]=[32]+[−42]=[−14]\mathbf{u} - 2\mathbf{v} = \begin{bmatrix} 3 \\ 2 \end{bmatrix} - 2\begin{bmatrix} 2 \\ -1 \end{bmatrix} = \begin{bmatrix} 3 \\ 2 \end{bmatrix} + \begin{bmatrix} -4 \\ 2 \end{bmatrix} = \begin{bmatrix} -1 \\ 4 \end{bmatrix}u−2v=[32]−2[2−1]=[32]+[−42]=[−14]
结论:
u+v=[51],u−2v=[−14]
\mathbf{u} + \mathbf{v} = \begin{bmatrix} 5 \\ 1 \end{bmatrix},\quad
\mathbf{u} - 2\mathbf{v} = \begin{bmatrix} -1 \\ 4 \end{bmatrix}
u+v=[51],u−2v=[−14]
3.
用箭头在 xyxyxy 平面上表示向量:
u,v,−v,−2v,u+v,u−v,u−2v\mathbf{u}, \mathbf{v}, -\mathbf{v}, -2\mathbf{v}, \mathbf{u}+\mathbf{v}, \mathbf{u}-\mathbf{v}, \mathbf{u}-2\mathbf{v}u,v,−v,−2v,u+v,u−v,u−2v。
注意 u−v\mathbf{u}-\mathbf{v}u−v 是三个顶点为 0,u,−v\mathbf{0}, \mathbf{u}, -\mathbf{v}0,u,−v 的平行四边形的另一个顶点。
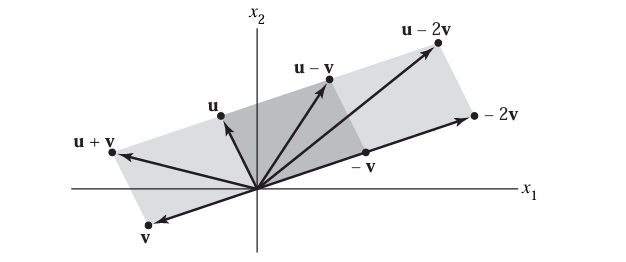
4.
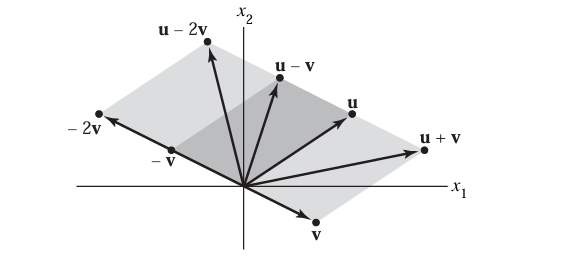
用箭头在 xyxyxy 平面上表示向量:
u,v,−v,−2v,u+v,u−v,u−2v\mathbf{u}, \mathbf{v}, -\mathbf{v}, -2\mathbf{v}, \mathbf{u}+\mathbf{v}, \mathbf{u}-\mathbf{v}, \mathbf{u}-2\mathbf{v}u,v,−v,−2v,u+v,u−v,u−2v。
(使用习题 2 中的 u\mathbf{u}u 和 v\mathbf{v}v)
5.
写出等价于向量方程的线性方程组:
x1[6−15]+x2[−340]=[−7−5−5] x_1\begin{bmatrix} 6 \\ -1 \\ 5 \end{bmatrix} + x_2\begin{bmatrix} -3 \\ 4 \\ 0 \end{bmatrix} = \begin{bmatrix} -7 \\ -5 \\ -5 \end{bmatrix} x16−15+x2−340=−7−5−5
等价线性方程组:
- 第一行:6x1−3x2=−76x_1 - 3x_2 = -76x1−3x2=−7
- 第二行:−x1+4x2=−5-x_1 + 4x_2 = -5−x1+4x2=−5
- 第三行:5x1+0x2=−55x_1 + 0x_2 = -55x1+0x2=−5
完整方程组:
{6x1−3x2=−7−x1+4x2=−55x1=−5
\begin{cases}
6x_1 - 3x_2 = -7 \\
-x_1 + 4x_2 = -5 \\
5x_1 = -5
\end{cases}
⎩⎨⎧6x1−3x2=−7−x1+4x2=−55x1=−5
6.
写出等价于向量方程的线性方程组:
x1[−2−2]+x2[85]+x3[1−6]=[00] x_1\begin{bmatrix} -2 \\ -2 \end{bmatrix} + x_2\begin{bmatrix} 8 \\ 5 \end{bmatrix} + x_3\begin{bmatrix} 1 \\ -6 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} x1[−2−2]+x2[85]+x3[1−6]=[00]
等价线性方程组:
- 第一行:−2x1+8x2+x3=0-2x_1 + 8x_2 + x_3 = 0−2x1+8x2+x3=0
- 第二行:−2x1+5x2−6x3=0-2x_1 + 5x_2 - 6x_3 = 0−2x1+5x2−6x3=0
完整方程组:
{−2x1+8x2+x3=0−2x1+5x2−6x3=0
\begin{cases}
-2x_1 + 8x_2 + x_3 = 0 \\
-2x_1 + 5x_2 - 6x_3 = 0 \\
\end{cases}
{−2x1+8x2+x3=0−2x1+5x2−6x3=0
9.
写出等价于线性方程组的向量方程:
{x2+5x3=04x1+6x2−x3=0−x1+3x2−8x3=0 \begin{cases} x_2 + 5x_3 = 0 \\ 4x_1 + 6x_2 - x_3 = 0 \\ -x_1 + 3x_2 - 8x_3 = 0 \end{cases} ⎩⎨⎧x2+5x3=04x1+6x2−x3=0−x1+3x2−8x3=0
等价向量方程:
x1[04−1]+x2[163]+x3[5−1−8]=[000]
x_1\begin{bmatrix} 0 \\ 4 \\ -1 \end{bmatrix} + x_2\begin{bmatrix} 1 \\ 6 \\ 3 \end{bmatrix} + x_3\begin{bmatrix} 5 \\ -1 \\ -8 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}
x104−1+x2163+x35−1−8=000
推导过程:
- 第一列对应 x1x_1x1 的系数:[0,4,−1]T[0, 4, -1]^T[0,4,−1]T
- 第二列对应 x2x_2x2 的系数:[1,6,3]T[1, 6, 3]^T[1,6,3]T
- 第三列对应 x3x_3x3 的系数:[5,−1,−8]T[5, -1, -8]^T[5,−1,−8]T
- 右侧为零向量 [0,0,0]T[0, 0, 0]^T[0,0,0]T
10.
写出等价于线性方程组的向量方程:
{4x1+x2+3x3=9x1−7x2−2x3=28x1+6x2−5x3=15 \begin{cases} 4x_1 + x_2 + 3x_3 = 9 \\ x_1 - 7x_2 - 2x_3 = 2 \\ 8x_1 + 6x_2 - 5x_3 = 15 \end{cases} ⎩⎨⎧4x1+x2+3x3=9x1−7x2−2x3=28x1+6x2−5x3=15
等价向量方程:
x1[418]+x2[1−76]+x3[3−2−5]=[9215]
x_1\begin{bmatrix} 4 \\ 1 \\ 8 \end{bmatrix} + x_2\begin{bmatrix} 1 \\ -7 \\ 6 \end{bmatrix} + x_3\begin{bmatrix} 3 \\ -2 \\ -5 \end{bmatrix} = \begin{bmatrix} 9 \\ 2 \\ 15 \end{bmatrix}
x1418+x21−76+x33−2−5=9215
推导过程:
- 第一列对应 x1x_1x1 的系数:[4,1,8]T[4, 1, 8]^T[4,1,8]T
- 第二列对应 x2x_2x2 的系数:[1,−7,6]T[1, -7, 6]^T[1,−7,6]T
- 第三列对应 x3x_3x3 的系数:[3,2,−5]T[3, 2, -5]^T[3,2,−5]T
- 右侧为常数向量 [9,2,15]T[9, 2, 15]^T[9,2,15]T
11.
确认向量 b\mathbf{b}b 是否是 a1,a2,a3\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3a1,a2,a3 的线性组合:
a1=[1−20], a2=[012], a3=[5−68], b=[2−16] \mathbf{a}_1 = \begin{bmatrix} 1 \\ -2 \\ 0 \end{bmatrix},\ \mathbf{a}_2 = \begin{bmatrix} 0 \\ 1 \\ 2 \end{bmatrix},\ \mathbf{a}_3 = \begin{bmatrix} 5 \\ -6 \\ 8 \end{bmatrix},\ \mathbf{b} = \begin{bmatrix} 2 \\ -1 \\ 6 \end{bmatrix} a1=1−20, a2=012, a3=5−68, b=2−16
增广矩阵:
[1052−21−6−10286]
\begin{bmatrix}
1 & 0 & 5 & 2 \\
-2 & 1 & -6 & -1 \\
0 & 2 & 8 & 6
\end{bmatrix}
1−200125−682−16
行变换过程:
-
将第二行替换为 R2+2R1R_2 + 2R_1R2+2R1:
[105201430286] \begin{bmatrix} 1 & 0 & 5 & 2 \\ 0 & 1 & 4 & 3 \\ 0 & 2 & 8 & 6 \end{bmatrix} 100012548236 -
将第三行替换为 R3−2R2R_3 - 2R_2R3−2R2:
[105201430000] \begin{bmatrix} 1 & 0 & 5 & 2 \\ 0 & 1 & 4 & 3 \\ 0 & 0 & 0 & 0 \end{bmatrix} 100010540230
结论:
b\mathbf{b}b 是 a1,a2,a3\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3a1,a2,a3 的线性组合。
例如:b=2a1+3a2+0a3\mathbf{b} = 2\mathbf{a}_1 + 3\mathbf{a}_2 + 0\mathbf{a}_3b=2a1+3a2+0a3。
12.
确认向量 b\mathbf{b}b 是否是 a1,a2,a3\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3a1,a2,a3 的线性组合:
a1=[1−22], a2=[055], a3=[208], b=[−511−7] \mathbf{a}_1 = \begin{bmatrix} 1 \\ -2 \\ 2 \end{bmatrix},\ \mathbf{a}_2 = \begin{bmatrix} 0 \\ 5 \\ 5 \end{bmatrix},\ \mathbf{a}_3 = \begin{bmatrix} 2 \\ 0 \\ 8 \end{bmatrix},\ \mathbf{b} = \begin{bmatrix} -5 \\ 11 \\ -7 \end{bmatrix} a1=1−22, a2=055, a3=208, b=−511−7
解题思路:
b\mathbf{b}b 是 a1,a2,a3\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3a1,a2,a3 的线性组合当且仅当存在标量 x1,x2,x3x_1, x_2, x_3x1,x2,x3 使得:
x1a1+x2a2+x3a3=b
x_1\mathbf{a}_1 + x_2\mathbf{a}_2 + x_3\mathbf{a}_3 = \mathbf{b}
x1a1+x2a2+x3a3=b
增广矩阵:
M=[102−5−25011258−7]
M = \begin{bmatrix}
1 & 0 & 2 & -5 \\
-2 & 5 & 0 & 11 \\
2 & 5 & 8 & -7
\end{bmatrix}
M=1−22055208−511−7
行变换过程:
-
将第二行替换为 R2+2R1R_2 + 2R_1R2+2R1:
[102−50541258−7] \begin{bmatrix} 1 & 0 & 2 & -5 \\ 0 & 5 & 4 & 1 \\ 2 & 5 & 8 & -7 \end{bmatrix} 102055248−51−7 -
将第三行替换为 R3−2R1R_3 - 2R_1R3−2R1:
[102−505410543] \begin{bmatrix} 1 & 0 & 2 & -5 \\ 0 & 5 & 4 & 1 \\ 0 & 5 & 4 & 3 \end{bmatrix} 100055244−513 -
将第三行替换为 R3−R2R_3 - R_2R3−R2:
[102−505410002] \begin{bmatrix} 1 & 0 & 2 & -5 \\ 0 & 5 & 4 & 1 \\ 0 & 0 & 0 & 2 \end{bmatrix} 100050240−512
相容性分析:
- 第三行对应方程 0x1+0x2+0x3=20x_1 + 0x_2 + 0x_3 = 20x1+0x2+0x3=2,即 0=20 = 20=2,为矛盾方程。
- 该矛盾表明方程组无解。
结论:
b\mathbf{b}b 不是 a1,a2,a3\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3a1,a2,a3 的线性组合。
13.
确定向量 b\mathbf{b}b 是否是矩阵 AAA 的各列向量的线性组合:
A=[1−42035−28−4],b=[3−7−3] A = \begin{bmatrix} 1 & -4 & 2 \\ 0 & 3 & 5 \\ -2 & 8 & -4 \end{bmatrix},\quad \mathbf{b} = \begin{bmatrix} 3 \\ -7 \\ -3 \end{bmatrix} A=10−2−43825−4,b=3−7−3
增广矩阵:
[1−423035−7−28−4−3]
\begin{bmatrix}
1 & -4 & 2 & 3 \\
0 & 3 & 5 & -7 \\
-2 & 8 & -4 & -3
\end{bmatrix}
10−2−43825−43−7−3
行变换过程:
- 将第三行替换为 R3+2R1R_3 + 2R_1R3+2R1:
[1−423035−70003] \begin{bmatrix} 1 & -4 & 2 & 3 \\ 0 & 3 & 5 & -7 \\ 0 & 0 & 0 & 3 \end{bmatrix} 100−4302503−73
相容性分析:
- 第三行对应方程 0x1+0x2+0x3=30x_1 + 0x_2 + 0x_3 = 30x1+0x2+0x3=3,即 0=30 = 30=3,为矛盾方程。
- 该矛盾表明方程组无解。
结论:
b\mathbf{b}b 不是矩阵 AAA 各列向量的线性组合。
14.
确定向量 b\mathbf{b}b 是否是矩阵 AAA 的各列向量的线性组合:
A=[1−2−60371−25],b=[11−59] A = \begin{bmatrix} 1 & -2 & -6 \\ 0 & 3 & 7 \\ 1 & -2 & 5 \end{bmatrix},\quad \mathbf{b} = \begin{bmatrix} 11 \\ -5 \\ 9 \end{bmatrix} A=101−23−2−675,b=11−59
增广矩阵:
[1−2−611037−51−259]
\begin{bmatrix}
1 & -2 & -6 & 11 \\
0 & 3 & 7 & -5 \\
1 & -2 & 5 & 9
\end{bmatrix}
101−23−2−67511−59
行变换过程:
- 将第三行替换为 R3−R1R_3 - R_1R3−R1:
[1−2−611037−50011−2] \begin{bmatrix} 1 & -2 & -6 & 11 \\ 0 & 3 & 7 & -5 \\ 0 & 0 & 11 & -2 \end{bmatrix} 100−230−671111−5−2
相容性分析:
- 无矛盾行,且所有主元存在。
- 方程组有解。
结论:
b\mathbf{b}b 是矩阵 AAA 各列向量的线性组合。
15.
写出属于 Span{v1,v2}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2\}Span{v1,v2} 的 5 个向量,并写出生成它们的权:
v1=[71−6], v2=[−530] \mathbf{v}_1 = \begin{bmatrix} 7 \\ 1 \\ -6 \end{bmatrix},\ \mathbf{v}_2 = \begin{bmatrix} -5 \\ 3 \\ 0 \end{bmatrix} v1=71−6, v2=−530
5 个向量及对应权:
- 0v1+0v2=[000]0\mathbf{v}_1 + 0\mathbf{v}_2 = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}0v1+0v2=000
- 1v1+0v2=[71−6]1\mathbf{v}_1 + 0\mathbf{v}_2 = \begin{bmatrix} 7 \\ 1 \\ -6 \end{bmatrix}1v1+0v2=71−6
- 0v1+1v2=[−530]0\mathbf{v}_1 + 1\mathbf{v}_2 = \begin{bmatrix} -5 \\ 3 \\ 0 \end{bmatrix}0v1+1v2=−530
- 1v1+1v2=[24−6]1\mathbf{v}_1 + 1\mathbf{v}_2 = \begin{bmatrix} 2 \\ 4 \\ -6 \end{bmatrix}1v1+1v2=24−6
- 1v1−1v2=[12−2−6]1\mathbf{v}_1 - 1\mathbf{v}_2 = \begin{bmatrix} 12 \\ -2 \\ -6 \end{bmatrix}1v1−1v2=12−2−6
16.
写出属于 Span{v1,v2}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2\}Span{v1,v2} 的 5 个向量,并写出生成它们的权:
v1=[302], v2=[−203] \mathbf{v}_1 = \begin{bmatrix} 3 \\ 0 \\ 2 \end{bmatrix},\ \mathbf{v}_2 = \begin{bmatrix} -2 \\ 0 \\ 3 \end{bmatrix} v1=302, v2=−203
5 个向量及对应权:
- 0v1+0v2=[000]0\mathbf{v}_1 + 0\mathbf{v}_2 = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}0v1+0v2=000
- 1v1+0v2=[302]1\mathbf{v}_1 + 0\mathbf{v}_2 = \begin{bmatrix} 3 \\ 0 \\ 2 \end{bmatrix}1v1+0v2=302
- 0v1+1v2=[−203]0\mathbf{v}_1 + 1\mathbf{v}_2 = \begin{bmatrix} -2 \\ 0 \\ 3 \end{bmatrix}0v1+1v2=−203
- 1v1+1v2=[105]1\mathbf{v}_1 + 1\mathbf{v}_2 = \begin{bmatrix} 1 \\ 0 \\ 5 \end{bmatrix}1v1+1v2=105
- 1v1−1v2=[50−1]1\mathbf{v}_1 - 1\mathbf{v}_2 = \begin{bmatrix} 5 \\ 0 \\ -1 \end{bmatrix}1v1−1v2=50−1
17.
设 a1=[14−2]\mathbf{a}_1 = \begin{bmatrix} 1 \\ 4 \\ -2 \end{bmatrix}a1=14−2, a2=[−2−37]\mathbf{a}_2 = \begin{bmatrix} -2 \\ -3 \\ 7 \end{bmatrix}a2=−2−37, b=[41h]\mathbf{b} = \begin{bmatrix} 4 \\ 1 \\ h \end{bmatrix}b=41h,当 hhh 取何值时 b\mathbf{b}b 在 Span{a1,a2}\text{Span}\{\mathbf{a}_1, \mathbf{a}_2\}Span{a1,a2} 内?
增广矩阵:
[1−244−31−27h]
\begin{bmatrix}
1 & -2 & 4 \\
4 & -3 & 1 \\
-2 & 7 & h
\end{bmatrix}
14−2−2−3741h
行变换过程:
-
R2←R2−4R1R_2 \leftarrow R_2 - 4R_1R2←R2−4R1,R3←R3+2R1R_3 \leftarrow R_3 + 2R_1R3←R3+2R1:
[1−2405−1503h+8] \begin{bmatrix} 1 & -2 & 4 \\ 0 & 5 & -15 \\ 0 & 3 & h+8 \end{bmatrix} 100−2534−15h+8 -
R2←15R2R_2 \leftarrow \frac{1}{5}R_2R2←51R2:
[1−2401−303h+8] \begin{bmatrix} 1 & -2 & 4 \\ 0 & 1 & -3 \\ 0 & 3 & h+8 \end{bmatrix} 100−2134−3h+8 -
R3←R3−3R2R_3 \leftarrow R_3 - 3R_2R3←R3−3R2:
[1−2401−300h+17] \begin{bmatrix} 1 & -2 & 4 \\ 0 & 1 & -3 \\ 0 & 0 & h+17 \end{bmatrix} 100−2104−3h+17
相容性条件:
- 为使方程组相容,需 h+17=0h + 17 = 0h+17=0,即 h=−17h = -17h=−17。
结论:
当且仅当 h=−17h = -17h=−17 时,b\mathbf{b}b 在 Span{a1,a2}\text{Span}\{\mathbf{a}_1, \mathbf{a}_2\}Span{a1,a2} 内。
18.
设 v1=[10−2]\mathbf{v}_1 = \begin{bmatrix} 1 \\ 0 \\ -2 \end{bmatrix}v1=10−2, v2=[−318]\mathbf{v}_2 = \begin{bmatrix} -3 \\ 1 \\ 8 \end{bmatrix}v2=−318, y=[h−5−3]\mathbf{y} = \begin{bmatrix} h \\ -5 \\ -3 \end{bmatrix}y=h−5−3,当 hhh 取何值时 y\mathbf{y}y 在 Span{v1,v2}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2\}Span{v1,v2} 内?
增广矩阵:
[1−3h01−5−28−3]
\begin{bmatrix}
1 & -3 & h \\
0 & 1 & -5 \\
-2 & 8 & -3
\end{bmatrix}
10−2−318h−5−3
行变换过程:
-
R3←R3+2R1R_3 \leftarrow R_3 + 2R_1R3←R3+2R1:
[1−3h01−5022h−3] \begin{bmatrix} 1 & -3 & h \\ 0 & 1 & -5 \\ 0 & 2 & 2h-3 \end{bmatrix} 100−312h−52h−3 -
R3←R3−2R2R_3 \leftarrow R_3 - 2R_2R3←R3−2R2:
[1−3h01−5002h+7] \begin{bmatrix} 1 & -3 & h \\ 0 & 1 & -5 \\ 0 & 0 & 2h+7 \end{bmatrix} 100−310h−52h+7
相容性条件:
- 为使方程组相容,需 2h+7=02h + 7 = 02h+7=0,即 h=−72h = -\frac{7}{2}h=−27。
结论:
当且仅当 h=−72h = -\frac{7}{2}h=−27 时,y\mathbf{y}y 在 Span{v1,v2}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2\}Span{v1,v2} 内。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








