线性代数及其应用习题答案(中文版)第一章 线性代数中的线性方程组 1.3 向量方程(2)

19.
对向量 ${\mathbf{v}}_1=\left[\begin{array}{c}8\\ 2\\ -6\end{array}\right]$, ${\mathbf{v}}_2=\left[\begin{array}{c}12\\ 3\\ -9\end{array}\right]$，给出 Span{v1,v2}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2\}Span{v1​,v2​} 的几何解释。

分析：

• 观察得 ${\mathbf{v}}_2=\frac{3}{2}{\mathbf{v}}_1$，说明 ${\mathbf{v}}_1$ 和 ${\mathbf{v}}_2$ 线性相关。
• Span{v1,v2}=Span{v1}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2\} = \text{Span}\{\mathbf{v}_1\}Span{v1​,v2​}=Span{v1​}。

几何解释：
Span{v1,v2}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2\}Span{v1​,v2​} 是 ${\mathbb{R}}^3$ 中通过原点和 ${\mathbf{v}}_1$ 的一条直线。

---

20.
对习题 16 中的向量 ${\mathbf{v}}_1=\left[\begin{array}{c}3\\ 0\\ 2\end{array}\right]$, ${\mathbf{v}}_2=\left[\begin{array}{c}-2\\ 0\\ 3\end{array}\right]$，给出 Span{v1,v2}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2\}Span{v1​,v2​} 的几何解释。

分析：

• 检查线性相关性：假设 $a{\mathbf{v}}_1+b{\mathbf{v}}_2=0$，则：
  $$\{\begin{array}{l}3a-2b=0\\ 2a+3b=0\end{array}\Rightarrow a=b=0$$
  表明 ${\mathbf{v}}_1$ 和 ${\mathbf{v}}_2$ 线性无关。

几何解释：
Span{v1,v2}\text{Span}\{\mathbf{v}_1, \mathbf{v}_2\}Span{v1​,v2​} 是 ${\mathbb{R}}^3$ 中通过原点的一个平面。
该平面由所有形如 $s{\mathbf{v}}_1+t{\mathbf{v}}_2$（$s,t\in \mathbb{R}$）的向量组成，且所有向量的第二分量均为 0，故位于 $xz$-平面内。

---

21.
设 $\mathbf{u}=\left[\begin{array}{c}-1\\ 2\end{array}\right]$, $\mathbf{v}=\left[\begin{array}{c}2\\ 1\end{array}\right]$，证明：对所有 $h$ 和 $k$，$\left[\begin{array}{c}h\\ k\end{array}\right]$ 属于 Span{u,v}\text{Span}\{\mathbf{u}, \mathbf{v}\}Span{u,v}。

证明过程：
考虑向量方程 $x_1\mathbf{u}+x_2\mathbf{v}=\left[\begin{array}{c}h\\ k\end{array}\right]$，其增广矩阵为：
$$\left[\begin{array}{ccc}-1& 2& h\\ 2& 1& k\end{array}\right]$$

行变换过程：

1. $R_1\leftarrow -R_1$：
   $$\left[\begin{array}{ccc}1& -2& -h\\ 2& 1& k\end{array}\right]$$

2. $R_2\leftarrow R_2-2R_1$：
   $$\left[\begin{array}{ccc}1& -2& -h\\ 0& 5& k+2h\end{array}\right]$$

3. $R_2\leftarrow \frac{1}{5}{R}_2$：
   $$\left[\begin{array}{ccc}1& -2& -h\\ 0& 1& \frac{k+2h}{5}\end{array}\right]$$

4. $R_1\leftarrow R_1+2R_2$：
   $$
   \begin{bmatrix}
   1 & 0 & \frac{-5h+2k+4h}{5} \
   0 & 1 & \frac{k+2h}{5}
   \end{bmatrix}

   \begin{bmatrix}
   1 & 0 & \frac{-h+2k}{5} \
   0 & 1 & \frac{k+2h}{5}
   \end{bmatrix}
   $$

结论：
方程组对任意 $h$ 和 $k$ 都有唯一解：
$$x_1=\frac{-h+2k}{5},x_2=\frac{k+2h}{5}$$
因此，对所有 $h$ 和 $k$，[hk]∈Span{u,v}\begin{bmatrix} h \\ k \end{bmatrix} \in \text{Span}\{\mathbf{u}, \mathbf{v}\}[hk​]∈Span{u,v}。

---

22.
构造一个 $3\times 3$ 无零元素的矩阵 $A$ 和 ${\mathbb{R}}^3$ 中的一个向量 $\mathbf{b}$，使得 $\mathbf{b}$ 不属于 $A$ 的列向量的生成集。

构造示例：
令
$$A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right],\mathbf{b}=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$$

验证：
增广矩阵：
$$\left[\begin{array}{cccc}1& 2& 3& 0\\ 4& 5& 6& 0\\ 7& 8& 9& 1\end{array}\right]$$

行变换过程：

1. $R_2\leftarrow R_2-4R_1$，$R_3\leftarrow R_3-7R_1$：
   $$\left[\begin{array}{cccc}1& 2& 3& 0\\ 0& -3& -6& 0\\ 0& -6& -12& 1\end{array}\right]$$

2. $R_2\leftarrow -\frac{1}{3}{R}_2$：
   $$\left[\begin{array}{cccc}1& 2& 3& 0\\ 0& 1& 2& 0\\ 0& -6& -12& 1\end{array}\right]$$

3. $R_3\leftarrow R_3+6R_2$：
   $$\left[\begin{array}{cccc}1& 2& 3& 0\\ 0& 1& 2& 0\\ 0& 0& 0& 1\end{array}\right]$$

结论：
第三行对应方程 $0=1$，矛盾。因此，$\mathbf{b}=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$ 不属于 Span{a1,a2,a3}\text{Span}\{\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3\}Span{a1​,a2​,a3​}。

---

23.
判断下列命题的真假：

a. 向量 $\left[\begin{array}{c}-4\\ 3\end{array}\right]$ 的另一种写法是 $[-43]$。
False。向量 $\left[\begin{array}{c}-4\\ 3\end{array}\right]$ 是列向量，而 $[-43]$ 是行向量。

b. 平面上对应于 $\left[\begin{array}{c}-2\\ 5\end{array}\right]$ 和 $\left[\begin{array}{c}-5\\ 2\end{array}\right]$ 的两点位于通过原点的一条直线上。
False。若两点与原点共线，则 $\left[\begin{array}{c}-5\\ 2\end{array}\right]$ 应为 $\left[\begin{array}{c}-2\\ 5\end{array}\right]$ 的标量倍，但 $\frac{-5}{-2}\ne \frac{2}{5}$。

c. 向量 $\frac{1}{2}\mathbf{v}$ 是向量 ${\mathbf{v}}_1$ 和 ${\mathbf{v}}_2$ 的线性组合。
True。若 $\mathbf{v}={\mathbf{v}}_1$，则 $\frac{1}{2}\mathbf{v}=\frac{1}{2}{\mathbf{v}}_1+0{\mathbf{v}}_2$。

d. 增广矩阵为 $[{\mathbf{a}}_1{\mathbf{a}}_2{\mathbf{a}}_3\mathbf{b}]$ 的线性方程组的解集与向量方程 $x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+x_3{\mathbf{a}}_3=\mathbf{b}$ 的解集相同。
True。这是向量方程与线性方程组的基本等价关系。

e. 集 Span{u,v}\text{Span}\{\mathbf{u}, \mathbf{v}\}Span{u,v} 总是表示通过原点的一个平面。
False。若 $\mathbf{u}$ 与 $\mathbf{v}$ 线性相关（如 $\mathbf{v}=k\mathbf{u}$），则 Span{u,v}\text{Span}\{\mathbf{u}, \mathbf{v}\}Span{u,v} 是一条直线而非平面。

---

24.
判断下列命题的真假：

a. 任意 5 个实数组成的数列是 ${\mathbb{R}}^5$ 中的一个向量。
True。${\mathbb{R}}^5$ 中的向量定义为 5 个实数组成的有序数组。

b. 向量 $\mathbf{u}$ 等于向量 $\mathbf{u}-\mathbf{v}$ 与向量 $\mathbf{v}$ 之和。
True。由向量加法定义：$(\mathbf{u}-\mathbf{v})+\mathbf{v}=\mathbf{u}$。

c. 在线性组合 $c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\cdots +c_p{\mathbf{v}}_p$ 中，系数 $c_1,c_2,\dots ,c_p$ 不能全为 0。
False。当所有系数为 0 时，线性组合结果为零向量，这在定义中是允许的。

d. 当 $\mathbf{u}$ 和 $\mathbf{v}$ 是非零向量时，Span{u,v}\text{Span}\{\mathbf{u}, \mathbf{v}\}Span{u,v} 包含通过 $\mathbf{u}$ 与原点的直线。
True。Span{u,v}\text{Span}\{\mathbf{u}, \mathbf{v}\}Span{u,v} 包含所有形如 $s\mathbf{u}+t\mathbf{v}$ 的向量，特别地，当 $t=0$ 时，包含直线 {su∣s∈R}\{s\mathbf{u} \mid s \in \mathbb{R}\}{su∣s∈R}。

e. 对应于增广矩阵 $[{\mathbf{a}}_1{\mathbf{a}}_2{\mathbf{a}}_3\mathbf{b}]$ 的线性方程组是否有解的问题等价于 $\mathbf{b}$ 是否属于 Span{a1,a2,a3}\text{Span}\{\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3\}Span{a1​,a2​,a3​} 的问题。
True。这是线性组合与线性方程组解的基本等价关系。

---

25.
设 $A=\left[\begin{array}{ccc}1& 0& -4\\ 0& 3& -2\\ -2& 6& 3\end{array}\right]$，$\mathbf{b}=\left[\begin{array}{c}4\\ 1\\ -4\end{array}\right]$，以 ${\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3$ 表示 $A$ 的各列，并设 W=Span{a1,a2,a3}W = \text{Span}\{\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3\}W=Span{a1​,a2​,a3​}。
a. $\mathbf{b}$ 是否属于 $W$？在 {a1,a2,a3}\{\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3\}{a1​,a2​,a3​} 中有多少个向量？
b. $\mathbf{b}$ 是否属于 $W$？$W$ 中有多少个向量？
c. 证明：${\mathbf{a}}_1$ 属于 $W$。

解答：

• a.

  • {a1,a2,a3}\{\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3\}{a1​,a2​,a3​} 中有 3 个向量。

  • 为判断 $\mathbf{b}\in W$，解方程 $x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+x_3{\mathbf{a}}_3=\mathbf{b}$。

  • 增广矩阵：
    $$\left[\begin{array}{cccc}1& 0& -4& 4\\ 0& 3& -2& 1\\ -2& 6& 3& -4\end{array}\right]$$

  • 行变换后得：
    $$\left[\begin{array}{cccc}1& 0& -4& 4\\ 0& 1& -\frac{2}{3}& \frac{1}{3}\\ 0& 0& 1& 2\end{array}\right]$$

  • 有解：$x_1=12$, $x_2=\frac{5}{3}$, $x_3=2$。

  • $\mathbf{b}\in W$。

• b.

  • $W$ 是 ${\mathbb{R}}^3$ 的子空间，包含无穷多个向量（因 ${\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3$ 线性无关，$W={\mathbb{R}}^3$）。
  • $\mathbf{b}\in W$，且 $W$ 有无穷多个向量。

• c.

  • ${\mathbf{a}}_1=1{\mathbf{a}}_1+0{\mathbf{a}}_2+0{\mathbf{a}}_3$。
  • 由线性组合的定义，a1∈Span{a1,a2,a3}=W\mathbf{a}_1 \in \text{Span}\{\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3\} = Wa1​∈Span{a1​,a2​,a3​}=W。
  • ${\mathbf{a}}_1\in W$。

---

26.
设 $A=\left[\begin{array}{ccc}2& 0& 6\\ -1& 8& 5\\ 1& -2& 1\end{array}\right]$，$\mathbf{b}=\left[\begin{array}{c}10\\ 3\\ 3\end{array}\right]$，$W$ 为 $A$ 的列向量的所有线性组合的集合。
a. $\mathbf{b}$ 是否属于 $W$？
b. 证明 $A$ 的第 3 列属于 $W$。

解答：

a.
$\mathbf{b}\in W$ 当且仅当存在标量 $x_1,x_2,x_3$ 使得：
$$x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+x_3{\mathbf{a}}_3=\mathbf{b}$$
其中 ${\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3$ 是 $A$ 的列向量。

增广矩阵：
$$\left[\begin{array}{cccc}2& 0& 6& 10\\ -1& 8& 5& 3\\ 1& -2& 1& 3\end{array}\right]$$

行变换过程：

1. 将第一行缩放为 $\frac{1}{2}{R}_1$：
   $$\left[\begin{array}{cccc}1& 0& 3& 5\\ -1& 8& 5& 3\\ 1& -2& 1& 3\end{array}\right]$$

2. 将第二行替换为 $R_2+R_1$，将第三行替换为 $R_3-R_1$：
   $$\left[\begin{array}{cccc}1& 0& 3& 5\\ 0& 8& 8& 8\\ 0& -2& -2& -2\end{array}\right]$$

3. 将第三行替换为 $R_3+\frac{1}{4}{R}_2$：
   $$\left[\begin{array}{cccc}1& 0& 3& 5\\ 0& 8& 8& 8\\ 0& 0& 0& 0\end{array}\right]$$

相容性分析：

• 无矛盾行（如 $0=k$，$k\ne 0$），方程组相容。

• 主元列：第 1 列、第 2 列 → 基本变量：$x_1,x_2$

• 自由变量：$x_3$（令 $x_3=t$）

• 通解：
  $$\{\begin{array}{l}{x}_1=5-3t\\ x_2=1-t\end{array}$$

结论：
$\mathbf{b}$ 是 $A$ 的列向量的线性组合，因此 $\mathbf{b}\in W$。

b.
$A$ 的第 3 列为 ${\mathbf{a}}_3=\left[\begin{array}{c}6\\ 5\\ 1\end{array}\right]$。

证明：
取标量 $c_1=0$，$c_2=0$，$c_3=1$，则：
$$c_1{\mathbf{a}}_1+c_2{\mathbf{a}}_2+c_3{\mathbf{a}}_3=0\cdot {\mathbf{a}}_1+0\cdot {\mathbf{a}}_2+1\cdot {\mathbf{a}}_3={\mathbf{a}}_3$$

结论：
$A$ 的第 3 列 ${\mathbf{a}}_3$ 是 ${\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3$ 的线性组合，因此 ${\mathbf{a}}_3\in W$。

---

27.
某矿业公司有两个矿，#1 矿每天生产 20 吨铜和 550 公斤银，#2 矿每天生产 30 吨铜和 500 公斤银。设 ${\mathbf{v}}_1=\left[\begin{array}{c}20\\ 550\end{array}\right]$，${\mathbf{v}}_2=\left[\begin{array}{c}30\\ 500\end{array}\right]$。

a. 向量 $5{\mathbf{v}}_1$ 有什么实际意义？

解答：
$5{\mathbf{v}}_1$ 表示 #1 矿连续生产 5 天的总产出。

• 铜：$5\times 20=100$ 吨
• 银：$5\times 550=2750$ 公斤

b. 写出表示该公司生产 150 吨铜与 2825 公斤银时各矿生产天数的向量方程。

解答：
设 #1 矿生产 $x_1$ 天，#2 矿生产 $x_2$ 天，则：
$$x_1{\mathbf{v}}_1+x_2{\mathbf{v}}_2=\left[\begin{array}{c}150\\ 2825\end{array}\right]$$
展开为线性方程组：
$$\{\begin{array}{l}20x_1+30x_2=150\\ 550x_1+500x_2=2825\end{array}$$
解答：
设 #1 矿生产 $x_1$ 天，#2 矿生产 $x_2$ 天，则：
$$x_1{\mathbf{v}}_1+x_2{\mathbf{v}}_2=\left[\begin{array}{c}150\\ 2825\end{array}\right]$$
展开为线性方程组：
$$\{\begin{array}{l}20x_1+30x_2=150\\ 550x_1+500x_2=2825\end{array}$$

c. 解 (b) 中的方程。

解答：
增广矩阵：
$$\left[\begin{array}{ccc}20& 30& 150\\ 550& 500& 2825\end{array}\right]$$
行变换过程：

1. $R_1\leftarrow \frac{1}{20}{R}_1$：
   $$\left[\begin{array}{ccc}1& 1.5& 7.5\\ 550& 500& 2825\end{array}\right]$$

2. $R_2\leftarrow R_2-550R_1$：
   $$\left[\begin{array}{ccc}1& 1.5& 7.5\\ 0& -325& -1300\end{array}\right]$$

3. $R_2\leftarrow -\frac{1}{325}{R}_2$：
   $$\left[\begin{array}{ccc}1& 1.5& 7.5\\ 0& 1& 4\end{array}\right]$$

4. $R_1\leftarrow R_1-1.5R_2$：
   $$\left[\begin{array}{ccc}1& 0& 1.5\\ 0& 1& 4\end{array}\right]$$
   解得：
   $x_1=1.5$（#1 矿生产 1.5 天），$x_2=4$（#2 矿生产 4 天）。
   验证：

• 铜：$20(1.5)+30(4)=30+120=150$ 吨
• 银：$550(1.5)+500(4)=825+2000=2825$ 公斤

---

28.
某蒸汽厂燃烧两种煤：无烟煤 (A) 和烟煤 (B)。

• 每吨煤 A 产生：27.6 百万焦耳热量、3100 克二氧化硫、250 克固体颗粒
• 每吨煤 B 产生：30.2 百万焦耳热量、6400 克二氧化硫、360 克固体颗粒

a. 若燃烧 $x_1$ 吨 A 和 $x_2$ 吨 B，总产热是多少？

解答：
总热量 = $27.6x_1+30.2x_2$ 百万焦耳。

b. 用向量表示总产出，并写出线性组合形式。

解答：
总产出向量为：
$$x_1\left[\begin{array}{c}27.6\\ 3100\\ 250\end{array}\right]+x_2\left[\begin{array}{c}30.2\\ 6400\\ 360\end{array}\right]$$
该向量的三个分量分别表示：

1. 热量（百万焦耳）
2. 二氧化硫排放量（克）
3. 固体颗粒污染物排放量（克）

c. 已知总产出为 [162, 23610, 1623]，求 $x_1,x_2$。

解答：
增广矩阵：
$$\left[\begin{array}{ccc}27.6& 30.2& 162\\ 3100& 6400& 23610\\ 250& 360& 1623\end{array}\right]$$
行变换结果：
$$\left[\begin{array}{ccc}1.000& 0& 3.900\\ 0& 1.000& 1.800\\ 0& 0& 0\end{array}\right]$$
解得：
$x_1=3.9$ 吨（无烟煤 A），$x_2=1.8$ 吨（烟煤 B）。
验证：

• 热量：$27.6(3.9)+30.2(1.8)=107.64+54.36=162$ 百万焦耳
• 二氧化硫：$3100(3.9)+6400(1.8)=12090+11520=23610$ 克
• 固体颗粒：$250(3.9)+360(1.8)=975+648=1623$ 克

---

29.
计算由下列质点组成的质点系的重心（见下图）：
$$\begin{array}{cc}\text{点}& \text{质量}\\ {\mathbf{v}}_1=(5,-4,3)& 2\text{ 克}\\ {\mathbf{v}}_2=(4,3,-2)& 5\text{ 克}\\ {\mathbf{v}}_3=(-4,-3,-1)& 2\text{ 克}\\ {\mathbf{v}}_4=(-9,8,6)& 1\text{ 克}\end{array}$$

解答：

• 总质量：$m=2+5+2+1=10$ 克

• 计算 $m_1{\mathbf{v}}_1+m_2{\mathbf{v}}_2+m_3{\mathbf{v}}_3+m_4{\mathbf{v}}_4$：
  $$\begin{array}{rl}2{\mathbf{v}}_1& =2(5,-4,3)=(10,-8,6)\\ 5{\mathbf{v}}_2& =5(4,3,-2)=(20,15,-10)\\ 2{\mathbf{v}}_3& =2(-4,-3,-1)=(-8,-6,-2)\\ 1{\mathbf{v}}_4& =1(-9,8,6)=(-9,8,6)\end{array}$$

  $$\text{总和}=(10+20-8-9,-8+15-6+8,6-10-2+6)=(13,9,0)$$

• 重心坐标：
  $$\bar{\mathbf{v}}=\frac{1}{10}(13,9,0)=\left(1.3,0.9,0\right)$$

结论：
质点系的重心坐标为 $(1.3,0.9,0)$。

---

30.
设 $\mathbf{v}$ 为习题 29 中的一组质点 ${\mathbf{v}}_1,\dots ,{\mathbf{v}}_k$ 的质心，$\mathbf{v}$ 是否属于 Span{v1,…,vk}\text{Span}\{\mathbf{v}_1, \dots, \mathbf{v}_k\}Span{v1​,…,vk​}？给出理由。

解答：

• 质心定义：$\mathbf{v}=\frac{1}{m}(m_1{\mathbf{v}}_1+m_2{\mathbf{v}}_2+\cdots +m_k{\mathbf{v}}_k)$，其中 $m=m_1+m_2+\cdots +m_k$

• 重写为：
  $$\mathbf{v}=\frac{m_1}{m}{\mathbf{v}}_1+\frac{m_2}{m}{\mathbf{v}}_2+\cdots +\frac{m_k}{m}{\mathbf{v}}_k$$

• 这是 ${\mathbf{v}}_1,\dots ,{\mathbf{v}}_k$ 的线性组合，系数为 $\frac{m_1}{m},\dots ,\frac{m_k}{m}$

结论：
v∈Span{v1,…,vk}\mathbf{v} \in \text{Span}\{\mathbf{v}_1, \dots, \mathbf{v}_k\}v∈Span{v1​,…,vk​}，因为质心是各质点位置的线性组合。

---

31.
一块密度和厚度均匀的三角形薄板，其三个顶点分别是 ${\mathbf{v}}_1=(0,1)$, ${\mathbf{v}}_2=(8,1)$, ${\mathbf{v}}_3=(2,4)$，且其质量为 3 克。

a. 求这块薄板的质心坐标 $(x,y)$。

解答：

• 总质量：$m=3+3+3=9$ 克

• 质心坐标：
  $$\bar{\mathbf{v}}=\frac{1}{9}(3{\mathbf{v}}_1+3{\mathbf{v}}_2+3{\mathbf{v}}_3)=\frac{1}{3}({\mathbf{v}}_1+{\mathbf{v}}_2+{\mathbf{v}}_3)$$

  $$=\frac{1}{3}\left((0,1)+(8,1)+(2,4)\right)=\frac{1}{3}(10,6)=\left(\frac{10}{3},2\right)$$

结论：
质心坐标为 $\left(\frac{10}{3},2\right)$。

b. 如何在三个顶点上分布额外的 6 克物质，使得薄板的"平衡点"与在三个顶点上有 1 克质量的薄板的质心重合？

解答：

• 目标质心：$(2,2)$

• 设在 ${\mathbf{v}}_1,{\mathbf{v}}_2,{\mathbf{v}}_3$ 上分别增加 $w_1,w_2,w_3$ 克物质，满足 $w_1+w_2+w_3=6$

• 新质心方程：
  $$\frac{1}{9}\left((3+w_1){\mathbf{v}}_1+(3+w_2){\mathbf{v}}_2+(3+w_3){\mathbf{v}}_3\right)=(2,2)$$

• 展开并化简得方程组：
  $$\{\begin{array}{l}(w_1+1)(0)+(w_2+1)(8)+(w_3+1)(2)=18\\ (w_1+1)(1)+(w_2+1)(1)+(w_3+1)(4)=18\end{array}$$
  即：
  $$\{\begin{array}{l}8w_2+2w_3=8\\ w_1+w_2+4w_3=12\end{array}$$

• 结合约束条件 $w_1+w_2+w_3=6$，解得：
  $w_1=3.5$, $w_2=0.5$, $w_3=2$

结论：
在 ${\mathbf{v}}_1=(0,1)$ 处加 3.5 克，在 ${\mathbf{v}}_2=(8,1)$ 处加 0.5 克，在 ${\mathbf{v}}_3=(2,4)$ 处加 2 克。

---

32.

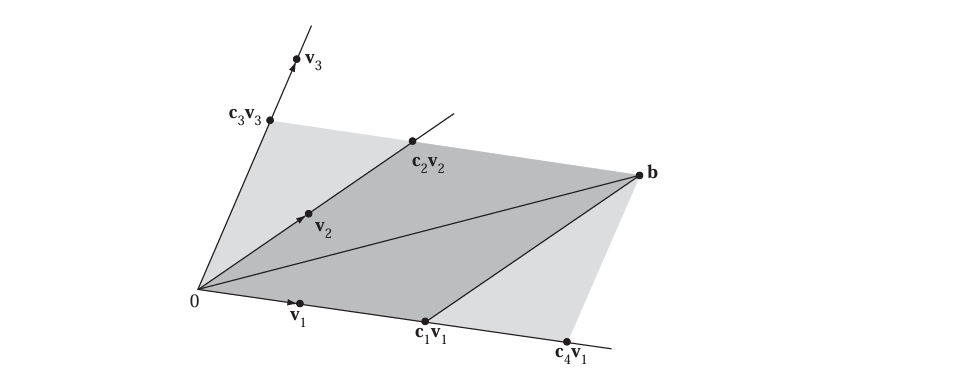
考虑 ${\mathbb{R}}^3$ 中的向量 ${\mathbf{v}}_1,{\mathbf{v}}_2,{\mathbf{v}}_3$ 和 $\mathbf{b}$。方程 $x_1{\mathbf{v}}_1+x_2{\mathbf{v}}_2+x_3{\mathbf{v}}_3=\mathbf{b}$ 是否有解？解是否唯一？使用图形给出解释。

解答：

• 从图形可知：
  • $\mathbf{b}$ 可表示为 ${\mathbf{v}}_1,{\mathbf{v}}_2,{\mathbf{v}}_3$ 的线性组合：$\mathbf{b}=c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+c_3{\mathbf{v}}_3$
  • $\mathbf{b}$ 也可表示为 ${\mathbf{v}}_1,{\mathbf{v}}_3,{\mathbf{v}}_4$ 的线性组合：$\mathbf{b}=c_4{\mathbf{v}}_1+0{\mathbf{v}}_2+c_3{\mathbf{v}}_3$
• 因此，方程至少有两个解：$(x_1,x_2,x_3)=(c_1,c_2,c_3)$ 和 $(x_1,x_2,x_3)=(c_4,0,c_3)$

结论：
方程有解，且解不唯一（实际上有无穷多解）。

---

33.
设 $\mathbf{u}=(u_1,u_2,\dots ,u_n)$, $\mathbf{v}=(v_1,v_2,\dots ,v_n)$, $\mathbf{w}=(w_1,w_2,\dots ,w_n)$，证明 ${\mathbb{R}}^n$ 的下列代数性质：
a. $(\mathbf{u}+\mathbf{v})+\mathbf{w}=\mathbf{u}+(\mathbf{v}+\mathbf{w})$
b. $c(\mathbf{u}+\mathbf{v})=c\mathbf{u}+c\mathbf{v}$，其中 $c$ 为任意实数。

证明：

a.
对任意 $j=1,2,\dots ,n$：
$$\begin{array}{rl}[(\mathbf{u}+\mathbf{v})+\mathbf{w}{]}_j& =(u_j+v_j)+w_j\\ & =u_j+(v_j+w_j)\text{(实数加法结合律)}\\ & =[\mathbf{u}+(\mathbf{v}+\mathbf{w}){]}_j\end{array}$$
由向量相等定义，$(\mathbf{u}+\mathbf{v})+\mathbf{w}=\mathbf{u}+(\mathbf{v}+\mathbf{w})$。

b.
对任意 $j=1,2,\dots ,n$：
$$\begin{array}{rl}[c(\mathbf{u}+\mathbf{v}){]}_j& =c(u_j+v_j)\\ & =c{u}_j+c{v}_j\text{(实数乘法分配律)}\\ & =[c\mathbf{u}+c\mathbf{v}{]}_j\end{array}$$
由向量相等定义，$c(\mathbf{u}+\mathbf{v})=c\mathbf{u}+c\mathbf{v}$。

结论：
${\mathbb{R}}^n$ 满足向量加法结合律和标量乘法分配律。

---

34.
设 $\mathbf{u}=(u_1,u_2,\dots ,u_n)$，证明 ${\mathbb{R}}^n$ 的下列代数性质：
a. $\mathbf{u}+(-\mathbf{u})=(-\mathbf{u})+\mathbf{u}=0$
b. $c(d\mathbf{u})=(cd)\mathbf{u}$，其中 $c,d$ 为任意实数。

证明：

a.
对任意 $j=1,2,\dots ,n$：
$$\begin{array}{rl}[\mathbf{u}+(-\mathbf{u}){]}_j& =u_j+(-u_j)=0\\ [(-\mathbf{u})+\mathbf{u}{]}_j& =(-u_j)+u_j=0\end{array}$$
由零向量定义，$\mathbf{u}+(-\mathbf{u})=(-\mathbf{u})+\mathbf{u}=0$。

b.
对任意 $j=1,2,\dots ,n$：
$$\begin{array}{rl}[c(d\mathbf{u}){]}_j& =c(d{u}_j)\\ & =(cd)u_j\text{(实数乘法结合律)}\\ & =[(cd)\mathbf{u}{]}_j\end{array}$$
由向量相等定义，$c(d\mathbf{u})=(cd)\mathbf{u}$。

结论：
${\mathbb{R}}^n$ 满足向量加法逆元律和标量乘法结合律。