好矩阵-腾讯音乐娱乐集团2023校园招聘技术类岗位编程题

本文探讨了一类特殊的大规模动态规划问题，通过寻找规律简化计算过程。以一个具体实例出发，详细阐述了如何利用矩阵特性及数学技巧，将复杂度极高的问题转化为易于解决的形式。文章还特别强调了在编程实现中应注意的数据类型溢出问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

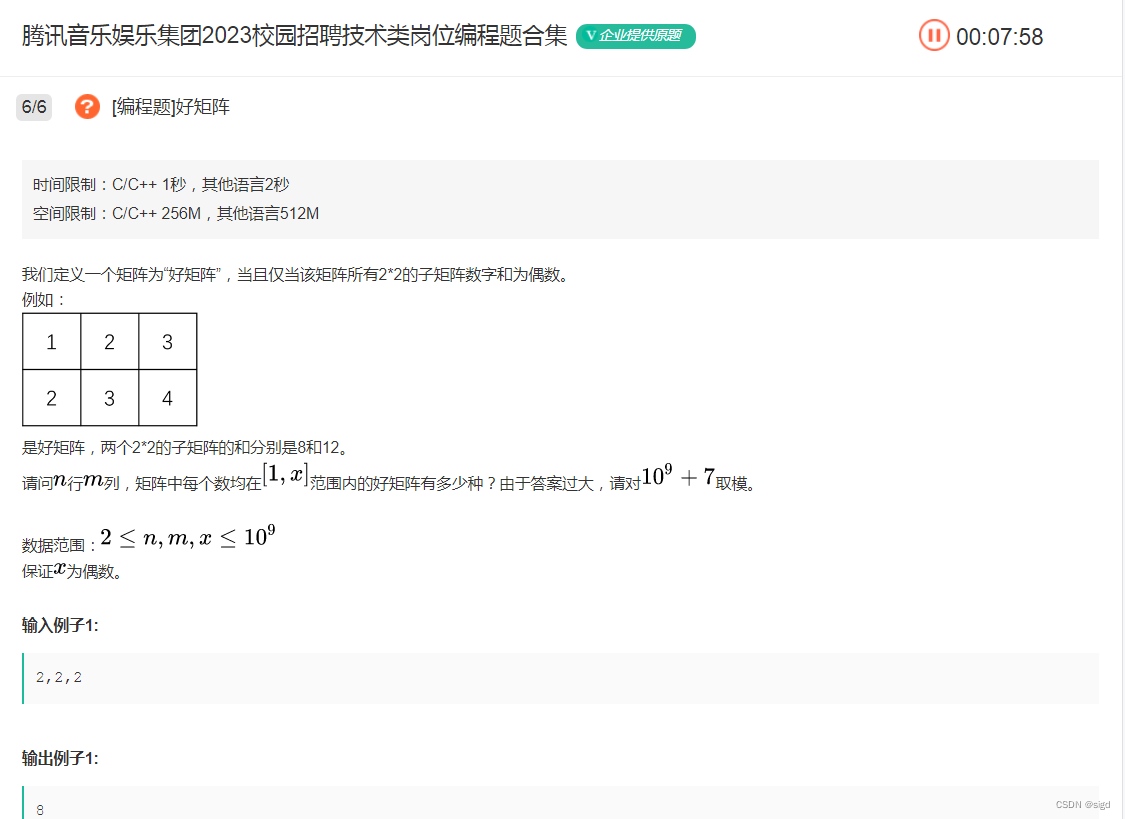
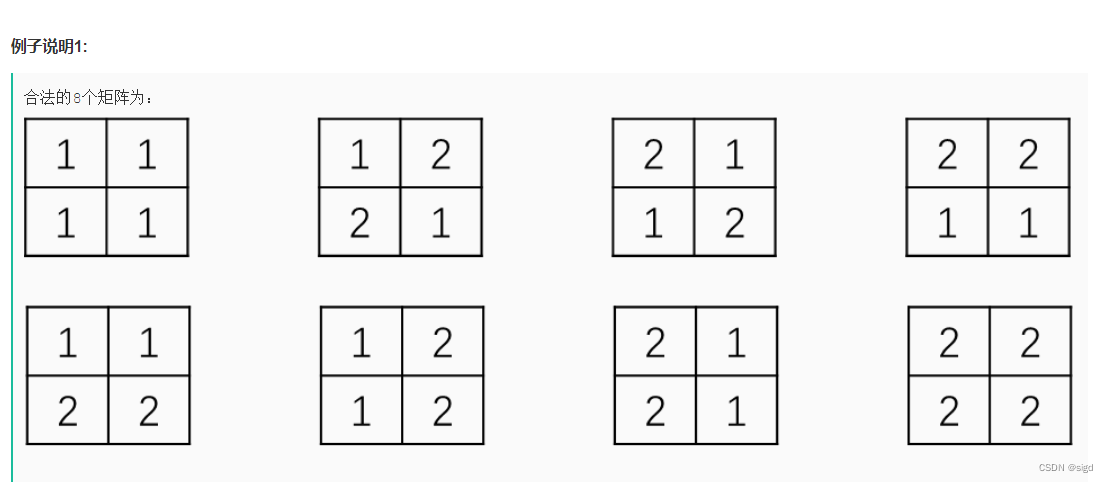
一般来说和方案数有关的问题均为动态规划问题，但此题目数据范围1e9，显然不可能去模拟或者用平方级的规划，必然是一道找规律的题目，注意x为偶数。

首先，矩阵的第一行应该没有任何限制，每个位置都可以有x种选择，因为无论怎么选，都可以想办法在第二行使得2*2矩阵满足要求。为了便于分析问题，随意选择了一种第一行情况。

因此，当第一行确定后（方案数A= $x^{m}$ ），后面每一行方案数只有两种选择：

（1）要不然每个元素都和上一行奇偶性一致（有x/2种选择），因为一行有m个元素，所以方案数为：第一行方案数A乘以B= $(\frac{x}{2})^{m}$ 。

（2）每个元素都和上一行奇偶性不一致，同样也是第一行方案数A乘以 $(\frac{x}{2})^{m}$ 。

那么归纳一下为A*B+A*B，即A*（2*B）。也就是每多一行，就要多乘一个2B。因为有n行，所以答案为 $A*(2B)^{n-1}$ 。

提交时错了几次，原因在于题目所给函数返回值为int，因此代码开始时所有类型都定义为int，但两个int做乘法时，其范围可能超过int范围，导致结果出错。（以下代码大部分正确，但仍有一个地方会导致int范围错误，读者可以此训练自己的代码检查能力）

class Solution {
public:
    long long ksm(int a,int b) /**< 递归实现快速幂 */
    {
        int mod=1e9+7;
        if(b==0)
            return 1;
        int  temp=ksm(a,b/2);
        if(b&1)
            return temp*temp%mod*a%mod;
        else
            return temp*temp%mod;
    }
    int numsOfGoodMatrix(int n, int m, int x) {
        /**<  第一行随意，方案总数x^m，第二行就要根据第一行值的“奇偶性"进行选择*/
        long long  A=ksm(x,m),B=ksm(x/2,m),mod=1e9+7;/**< 第一行求出来 */
        return A*ksm(2*B,n-1)%mod;
    }
};