求最大递减数列（导弹拦截问题）

例题：某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。
但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，
但是以后每一发炮弹都不能高于前一发的高度。
某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度，计算这套系统最多能拦截多少导弹，
                    如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
                    需要一个数组承接导弹数
                    需要一个变量来承接最大数值

样例：

输入：

389 207 155 300 299 170 158 65

输出：6  2

这题有两问，暂时先看第一问，一套系统最多可以拦截多少导弹。我们知道每次炮弹只能越来越低。也就说拦截的这些炮弹高度肯定是越来越低的。

如果题目给我们一组导弹飞来的高度数据，我们要算最多的拦截数量，也就是说我们要找到这组数里的一个最大的递减子序列。如样例中最大递减子序列应该是389 300 299 170 158 65 。

方法1：看到数据的时候，我们会想把数据分成好几个递减序列

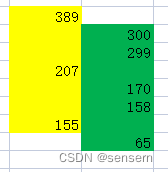就像这个样子，最终目的是经过的点最多。竖着可能记不太起来，横过来看就有点印象了。

 是不是有点像之前的过河卒问题，需要到某个地方，但是这里不同的是不一定是从左上角开始走，不过也可以采取类似的做法。我们将数据放在每个格子里，每个格子可以有两种情况到达，一个是左边过来，一个是上面下来，那么过这个格子的路线最多过几个点呢，那就看看是左边来的路线过点多还是上边来的路线过点多。最后我们看看那个点记录路过的点最多，那个那个值就是最大递减子序列的个数。

思路：先将数据分行存储进数组。

a[10][1000]=0//假设数据小于1000,小于10次递减序列。

b[n]//假设数据存储在b中,元素个数为n

for(i=0,j=-1,tp=0;i<n;i++)

{  if(b[i]>tp)

    j++;    //将数据存入a数组中，用tp记录上一个高度，如果b[i]大于tp说明遇到了一个新的递减序列，需要换行存储。这里存储是将b[i]存储在对应数组位置上加1，例如某个数据b[i]=7,那么在b[j][7]中自增一下，表示有这里有一个数据。

b[j][a[i]]++;tp=b[i]；

}

//然后将a数组处理一下，用c[10][1000]记录路线经过的点。

if(a[0][max]) c[0][max]=1;

for(w=max-1;w>=0;w--)//将第一行先算好。

  c[0][w]=c[0][w+1]+a[0][w];

for(q=1;q<=j;q++)

 c[q][max]=c[q-1][max]+a[q][max];

mas=0;

for(q=0;q<=j;q++)

  for(w=max;w>=0;w--)

      {c[q][w]=a[q][w]+max(c[q-1][w],c[q][w+1]);//某个点的过点数看看是左边来的多还是上面来的多，再加上自己的点数。

if(c[q][w]>mas) mas=c[q][w];

}

//最后mas就是我们要的结果。

  

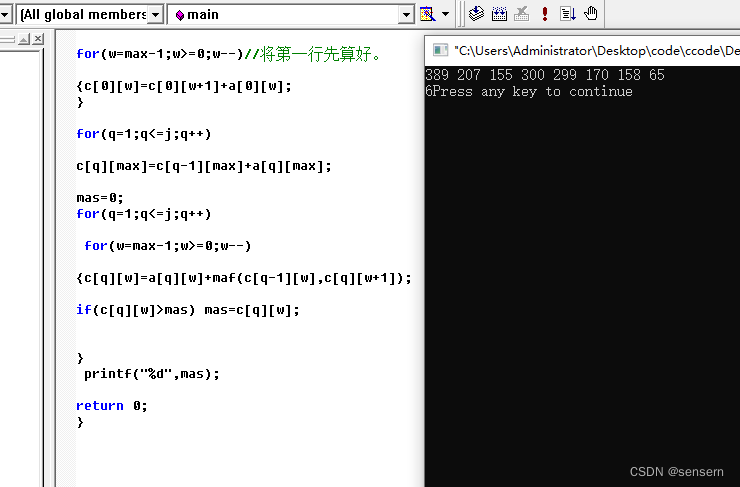
 代码：//这里只输入8个数据，作为测试样例

#include <stdio.h>
int  maf(int x,int y)
{
    if(x>y) return x;
    else return y;
}

int main(){
    int a[10][1000]={0},b[1000]={0},c[10][1000]={0},i,j,n=0,q,w,mas=0,max=0,tp;
    for(i=0;i<8;i++)
    {scanf("%d",&b[i]);
    n++;
    if (max<b[i]) max=b[i];
    }

    for(i=0,j=-1,tp=0;i<n;i++)
    {   
        if(b[i]>tp)
        j++; 
        a[j][b[i]]++;tp=b[i];
        
    }
    if(a[0][max]) c[0][max]=1;

for(w=max-1;w>=0;w--)//将第一行先算好。

{c[0][w]=c[0][w+1]+a[0][w];
}

for(q=1;q<=j;q++)

c[q][max]=c[q-1][max]+a[q][max];

mas=0;
for(q=1;q<=j;q++)

 for(w=max-1;w>=0;w--)

{c[q][w]=a[q][w]+maf(c[q-1][w],c[q][w+1]);

if(c[q][w]>mas) mas=c[q][w];

}
 printf("%d",mas);

return 0;
}
方法2：枚举法。我们可以将所有例子列举出来，选出我们需要的结果，但是，我们这里只需要结果，那我们就只需要枚举结果即可。那我们应该怎么枚举结果呢，首先我们想想怎么将这么多情况分类，似乎有点多，不太好分类，我们想想一种情况下，有那几个东西，开头点，中间经过的点，结束点。而结束点，才能知道我们需要的结果，开头点和中间点是不知道结果的。那我们就从结果点来分类。假设以某点b[i]为结果的线路，最大路过点为a[i]，那以下一个点为结果的线路里，最大的会有多少呢？这个结果肯定会是前面比b[i+1]大的一个点中，a[i]最大的那个，再加上自己。

思路：

 for(i=0;i<n;i++)

 a[i+1]=max(i+1)+1;//假设max是求前i+1个中比b[i+1]小的，且a最大的一个。

这样最大的a就是我们要的结果。

 

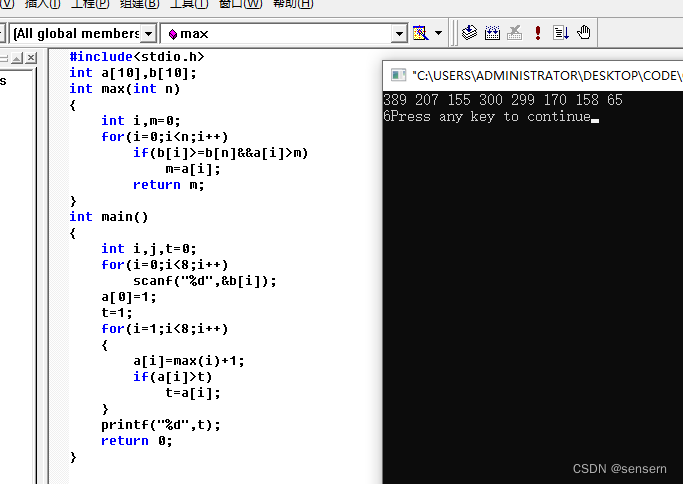
  代码：

#include<stdio.h>
int a[10],b[10];
int max(int n)
{
    int i,m=0;
    for(i=0;i<n;i++)
        if(b[i]>=b[n]&&a[i]>m)
            m=a[i];
        return m;
}
int main()
{
    int i,j,t=0;
    for(i=0;i<8;i++)
        scanf("%d",&b[i]);
    a[0]=1;
    t=1;
    for(i=1;i<8;i++)
    {
        a[i]=max(i)+1;
        if(a[i]>t)
            t=a[i];
    }
    printf("%d",t);
    return 0;
}