排列组合 小球入框类

例题：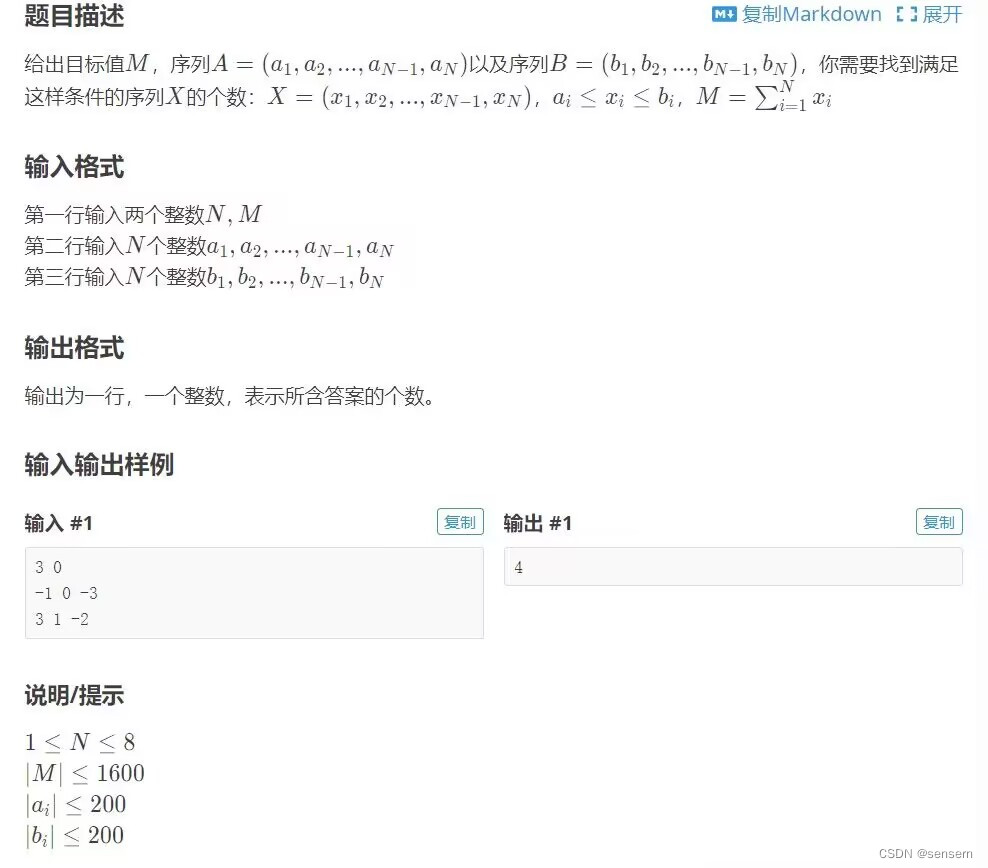

 题目解析：xi在ai和bi之间波动，似乎是将波动情况相乘就行，对每个xi有bi-ai+1种情况，但是题目还有一个限制，那就是xi的和为M。那我们将题目转化一下，将每个xi看作一个框，有若干个小球，随机放入框中，但是每个框有一个放入小球的上限。那我们知道就有N个框，每个框小球上限是bi-ai个，最少是0个，并且总共有多少个球呢，是M个吗，应该是M减去所有ai的和。因为我们知道xi的和是M，即=M,而是总球数，所以总球数等于。

那我们怎么去计算在有限制的情况下小球放入框中的情况数呢？我们会想到穷举法，但是似乎太多了，我们尝试用递归来解决。

首先  a[N].b[N],M,C[N]数据准备好。C[N]=b[N]-a[iN表示两者之差，即框的球数上限

我们先想想我们需要的递归函数得到什么东西，需要传递什么东西

得到在M个球放入有限制的这N个框的情况，那返回值是情况数量，需要的东西是总球数M和框数N。

int  qiu(int M,int N)//表示求在前N个有限制的框中放入M个球的情况。

然后是中间过程，我们要求前N个框放M个球应该怎么求，首先这第N个框有多少种情况，从0到ci这些情况。那这第N个框的每种情况是不是对应的剩下球有其他情况，假设第N框有三种情况，0，1，2。假设N框为0时，剩下球放入其他框有t种情况，N为1时，其他有y种情况，n为2时其他有u种情况，那所有情况数是不是t+y+u;那我们知道怎么求出N个框放M个球了。

qiu(M,N)=qiu(M,N-1)+qiu(M-1,N-1)+qiu(M-2,N-1).....

代码： sum=0;

  for(k=0;k<=cn;k++)

     sum+=qiu(m-k,n-1);//sum即为所求的qiu(m,n),

但是这里忽略了一个情况，那就是可能球数m可能小于cn，即使全部分给cn也不够，所以应该加一句k<=m

代码： sum=0;

  for(k=0;k<=cn&&k<=m;k++)

     sum+=qiu(m-k,n-1);//sum即为所求的qiu(m,n),

然后就是边界条件，有两个边界,m,n

对于M的边界，那就是m为0时，那就只有1种情况，都空着。

对于N的边界，那就是N为1时，这时候只有一个框，如果球大于上限，那么这种情况不行，返回0，否则也只有1个框装下所有球这种情况。

代码：

if(m==0)

  return 1;

if( n==1)

  if(m>c[n])

   return 0;

else return 1;

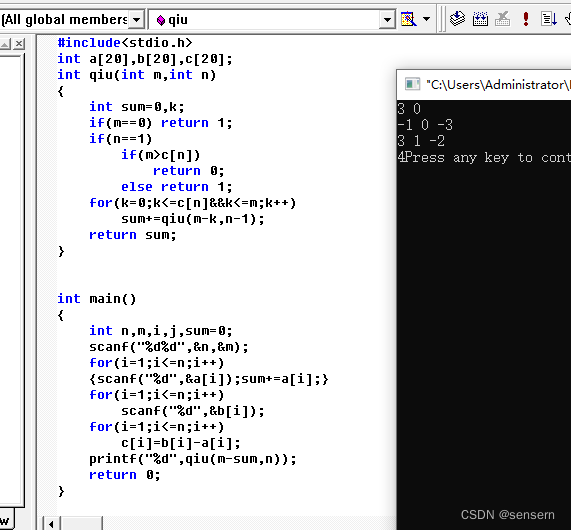
代码组合：

 

#include<stdio.h>
int a[20],b[20],c[20];
int qiu(int m,int n)
{
    int sum=0,k;
    if(m==0) return 1;
    if(n==1) 
        if(m>c[n])
            return 0;
        else return 1;
    for(k=0;k<=c[n]&&k<=m;k++)
        sum+=qiu(m-k,n-1);
    return sum;
}

    
int main()
{
    int n,m,i,j,sum=0;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)
    {scanf("%d",&a[i]);sum+=a[i];}
    for(i=1;i<=n;i++)
        scanf("%d",&b[i]);
    for(i=1;i<=n;i++)
        c[i]=b[i]-a[i];
    printf("%d",qiu(m-sum,n));
    return 0;
}