基于PyTorch的深度学习基础课程之九：分类模型评价指标（3|3）

本文详细讨论了分类模型的常用评价指标，包括准确率、平均准确率、混淆矩阵、精确率、召回率、F1值和AUC等。对这些指标含义的理解和运用，尤其是在不平衡样本数据集上的应用，是设计恰当模型和指导AI大模型调整模型需要掌握的知识。对这些指标的讨论采用了示例入手、逐步推进的方式，便于读者理解。

在本专栏的前述文章里，对分类模型的评价采用了最简单的准确率。本文详细讨论分类模型的常用评价指标。无论是自己设计模型，还是指导AI大模型去调整模型，评价指标显然是必须理解的内容。

本文仍然采用示例入手的分析方法，便于读者理解。读者也可暂时跳过公式推导部分，先掌握应用方法。

6 AUC(Area under the Curve)

在样本类别分布不平衡带来的评价问题上，AUC有很好的评价效果。AUC的全称是Area under the Curve，即曲线下的面积，这条曲线便是ROC曲线，它的全称为the Receiver Operating Characteristic曲线，直译过来为：受试者工作曲线。在上世纪50年代的电信号分析中最开始使用。ROC曲线有一个重要特性：当测试集中正负样本的分布发生变化时，该曲线能够保持不变。

ROC是以假正率FPR为横坐标，以真正率TPR为纵坐标的一条曲线，FPR和TPR的取值范围都是[0,1]，ROC曲线示例如图9-1所示。

图9-1 ROC曲线示例

ROC曲线的含义是什么呢？

先来看一条特殊的曲线。图9-1中，Random是一条连接原点到点(1,1)的直线，Random上的点的模坐标与纵坐标相等，也就是说FPR与TPR相等，不妨以Random上的点c(0.5,0.5)为例来看看该直线的含义。如果点c表示某个模型的预测能力，那么，该模型的假正率FPR和真正率TPR都为0.5，这意味着该模型对样本的预测类似于抛硬币，不管样本的特征是什么，随机等概打上正负标签即可。再来看Random上的点e(0.25,0.25)，它表示的模型则是对样本的预测类似掷一个四面的骰子，随机掷出指定的一面，则为正类，否则为负类，也就是说，该模型是按0.25的概率来随机给样本打正标签。因此，Random直线表示的模型是以一定概率来进行随机预测，原点表示所有的样本都按概率0判断为正类，点(1,1)表示所有的样本都按概率1判断为正类。这样的模型并没有什么实际意义。

再看Random上方的点，以点c正上方的b为例。点b表示的模型在真正率TPR上有了提高，不再是随机打标签了，提高了对正类实例的预测能力。而对于Random下方的点，表示预测能力比随机猜测还要差，这并没有讨论的意义。因此，只有位于Random上方的点代表的模型才具有实际的分类能力。像点a这样TPR为1的点代表的模型对正类样本的预测能力达到了完美，即能够全部预测出来。而FPR为0的点代表的模型对负类样本的预测能力达到了完美。它们的交叉点(0,1)代表的模型对正负两类样本都能够全部正确预测出来，是最完美的模型。因此，要尽量使模型靠近点(0,1)，即要同时使FPR趋近于0和使TPR趋近于1。

但是，对于一个分类模型来说，它的FPR和TPR是有关联的，并不能在使一个指标改善的同时也使另一个得到改善。分类模型的FPR和TPR的关联性如图9-1中的ROC曲线所示，提高一个指标同时会降低另一个指标。

如何得到ROC曲线呢？

从概率论的角度来看，模型关于每个样本的预测都存在一个概率值，好的模型就是要将原本为正类的样本判定为正的概率尽量大，而原本为负类的样本判定为正的概率尽量小。不同的模型学到的知识不同（提取的特征、采用的算法等因素影响），关于每个样本的预测概率也不同。模型对样本进行预测的概率分布如图9-2所示意。

图9-2 二分类模型对样本进行预测的概率分布示意图

图9-2中，横坐标表示某模型将样本预测为正的概率，纵坐标表示样本数量，正类曲线上的点(x,y)表示有y个正样本会以x大小的概率被预测为正样本，负类曲线上的点(x,y)表示有y个负样本会以x大小的概率被预测为正样本。如果对概率设定一个阈值，当大于该阈值的样本判定为正（图中阈值右边部分），那么随着阈值的变化判定为正的样本数量也会变化。对正类曲线来说，阈值右边部分（横线阴影部分）的面积是所有判定为正的正样本的数量，即TP。对负类曲线来说，阈值右边部分（斜线阴影部分)的面积是所有判定为正的负样本的数量，即FP。从图中可以看出，随着阈值的变化，TP和FP会同时变大，或者同时变小，这正是FPR和TPR不能同时得到改善的原因。

当阈值从1取到0时，可以得到一系列FP与TP值，并除以所有正类样本数量和负类样本数量，从而得到一系列FPR和TPR值对，它们的变化范围是从0到1。以FPR为横坐标值，以TPR为纵坐标值，将这些FPR和TPR值对作点画出来，就得到了图9-1中的ROC曲线。对于图9-1中的c点和(0,1)点代表的分类模型如图9-3中左、右两图所示。

图9-3 二分类模型对样本预测概率分布的特殊情况

好的分类模型是尽量使图9-2中正类曲线和负类曲线离得远的模型，它的ROC曲线也会更接近(0,1)点。图9-1中，ROC’曲线代表的模型比ROC曲线代表的模型就要更好一点，此时，该曲线下的面积就要更大，即AUC更大。

因为ROC曲线的坐标轴采用的是样本的比例值，因此即使正负样本的类别分布发生变化，ROC曲线也会保持不变，也就是说，AUC不会受样本分类不平衡的影响。因此AUC常用来评价类别不平衡的模型。

如何来实际计算AUC值呢？

首先分类模型要能给出每个样本的预测概率，这可以通过在神经网络的最后一层采用softmax等激活函数来实现。然后，统计出每个概率值的正类和负类样本数量，得到如图9-2所示的样本概率分布（实际应用中，概率值不是连续的，得到的正类曲线和负类曲线也不是连续的）。

根据样本概率分布，将阈值从1取到0，由得到的FPR和TPR值对作点画出ROC曲线，当然，实际应用中的ROC曲线不是一条连续的平滑曲线，而是一条锯齿状的ROC曲线（如图9-4中右图所示），计算该曲线下的面积即为AUC值。

图9-4 预测概率分布和ROC曲线示例

来看一个示例。假设有19个样本，它们的标签和模型的预测概率值如下：

标签：0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1；

预测概率值：0.1,0.2,0.2,0.3,0.3,0.4,0.5,0.7,0.9,0.15,0.45,0.55,0.75,0.75,0.85,0.95,0.75,0.85,0.95。

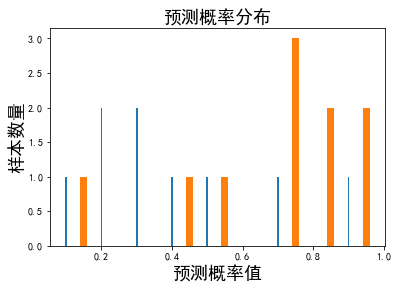
画出它们的概率分布图如图9-4左图所示，图中细线表示负类样本的数量，粗线表示正类样本的数量。利用sklearn.metrics包中的roc_curve（）函数计算出各点的fpr和tpr对，将它们代表的点依次连上，画出ROC曲线如图9-4右图所示。实现以上过程的代码见代码9-2。

代码9-2 AUC示例

import pandas as pd
import matplotlib.pyplot as plt

##### 样本的标签值和预测概率
data = {'label':[0,   0,   0,   0,   0,   0,   0,   0,   0,   1,    1,    1,    1,    1,    1,    1,    1,    1,    1],
        'proba':[0.1, 0.2, 0.2, 0.3, 0.3, 0.4, 0.5, 0.7, 0.9, 0.15, 0.45, 0.55, 0.75, 0.75, 0.85, 0.95, 0.75, 0.85, 0.95]}
df = pd.DataFrame(data)
len(df)
#>>> 19

##### 画出概率分布图
group = df.groupby(['label', 'proba']) # 按标签值和概率值分组
la0 = group.size()[0] # 负类样本概率值统计数
la1 = group.size()[1] # 正类样本概率值统计数

x0 = [] # 负类样本概率值
y0 = [] # 负类样本概率值对应的样本数量
for index, val in la0.items():
    x0.append(index)
    y0.append(val)

x1 = []
y1 = []
for index, val in la1.items():
    x1.append(index)
    y1.append(val)
    
plt.rcParams['font.sans-serif']=['SimHei'] # 设置字体为黑体
plt.rcParams['axes.unicode_minus']=False 
p1 = plt.bar(x0, height=y0, width=0.005) # 细线表示负类样本分布
p2 = plt.bar(x1, height=y1, width=0.02) # 组线表示正类样本分布
plt.xlabel('预测概率值', size=18)
plt.ylabel('样本数量', size=18)
plt.title('预测概率分布', size=18)
#>>> Text(0.5, 1.0, '预测概率分布')

##### 计算FPR和TPR对，并画出ROC曲线
from sklearn import metrics

fpr, tpr, thresholds = metrics.roc_curve(df['label'].values, df['proba'].values, pos_label=1)

plt.plot(fpr, tpr, marker='o')
plt.xlabel('False Positive Rate', size=18)
plt.ylabel('True Positive Rate', size=18)
plt.title('ROC Curve', size=18)
#>>> Text(0.5, 1.0, 'ROC Curve')

print("auc = " + str(metrics.auc(fpr, tpr))) # metrics.auc函数是以梯形法则求出ROC曲线与横坐标所夹面积
#>>> auc = 0.8

来验证一下ROC曲线。

当阈值大于0.95时，统计可知FP为0 、TP为0，因此FPR和TPR分别也为0，对应图中左侧第1个点。

当阈值等于0.95时，统计可知FP为0 、TP为2，再除以负类样本总数和正类样本总数，得到FPR和TPR分别为0和0.2，对应图中第2个点。

当阈值等于0.9时，统计可知FP为1、TP为2，计算得到得到FPR和TPR分别为0.11和0.2，对应图中第3个点。

如此，可验证全部ROC曲线上的点。

sklearn.metrics包提供了直接计算AUC的函数auc（），它是以梯形法则求出ROC曲线下的面积，计算得到示例中的AUC值为0.8。

计算本文示例的AUC值的代码见代码9-1.5。

代码9-1.5 计算AUC值

### 10. 计算AUC值
print('ROC曲线和AUC值:')
print('-' * 40)

# 使用sklearn的roc_auc_score
auc_score = metrics.roc_auc_score(all_labels, all_probabilities)
print(f"AUC值 (sklearn): {auc_score:.4f}")

# 使用sklearn的roc_curve
fpr, tpr, thresholds = metrics.roc_curve(all_labels, all_probabilities)

# 可视化ROC曲线
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC曲线 (AUC = {auc_score:.4f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--', label='随机猜测')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正率 (False Positive Rate)')
plt.ylabel('真正率 (True Positive Rate)')
plt.title('受试者工作曲线 (ROC Curve)')
plt.legend(loc="lower right")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

输出：

ROC曲线和AUC值:
----------------------------------------
AUC值 (sklearn): 0.9983