本文介绍了求和因子法在处理递归和式中的应用，涉及Rn的定义，如何通过a+bk求和，以及调和数的性质。讨论了多重和式计算策略，包括扰动法和差分算子在解决和式中的关键作用，特别是对阶乘幂和分部求和法的强调。
和式和递归式（复习时再动手算一下）——求和因子法
如果S0=a0，Sn=Sn-1+an，且an是一个n的倍数+一个常数（γn+β），则可转化为：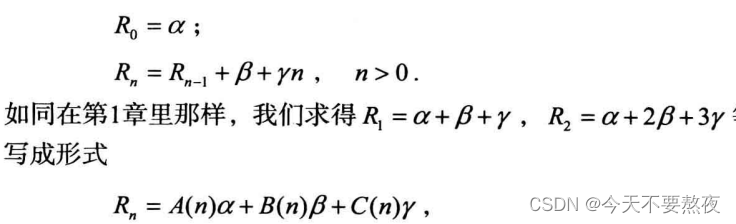
这里令Rn分别为1，n和n方，计算得出A(n)B(n)和C(n)
这里想要计算a+bk的和式，找到对应的R0为a即α，an为a+bn，则β为a，γ为b
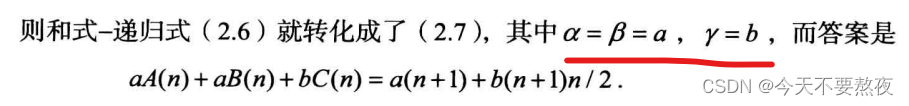
此外对于形如
利用公式可以得到
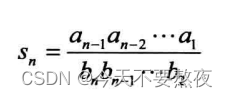
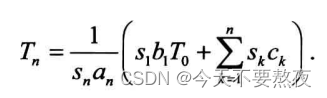
例如下式中an=n，bn=n+1，cn=2n
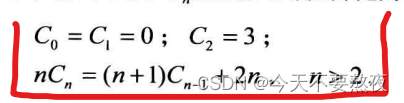
这里需要注意的是分界点n>2（书上P39）
调和数及性质
证明如下等式（必须掌握）
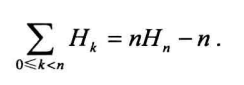
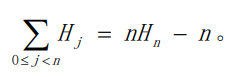
要通过一个多重和式来计算
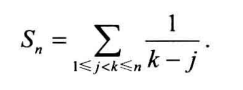
如果要证明的式子左边是j，那么求和顺序为先求k再求j于是最后就会出现j的形式（对谁求和就替换谁）
若先求的是j
这样就搞出了等式的左边，那么等式的右边就需要：
同理或者可以先用k-j替换j，然后先求和k
扰动法（加一个尾再甩出一个头）
对于例子：
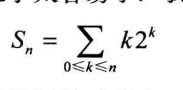利用扰动法可以解决：
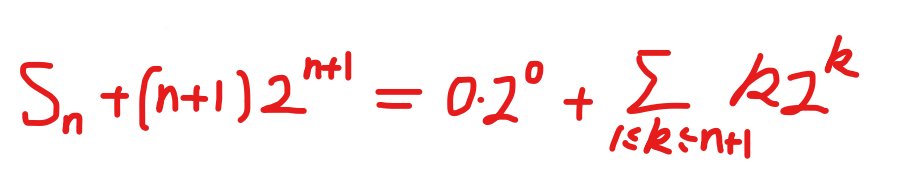
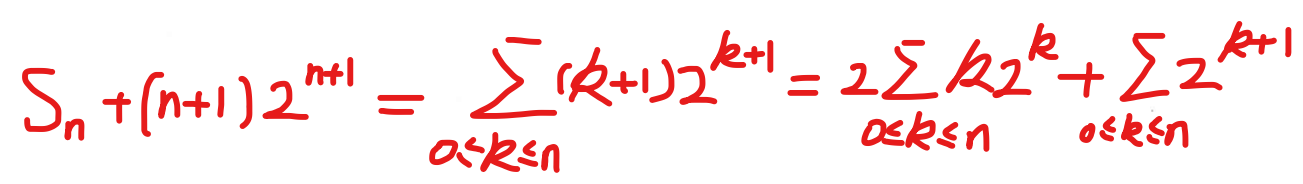
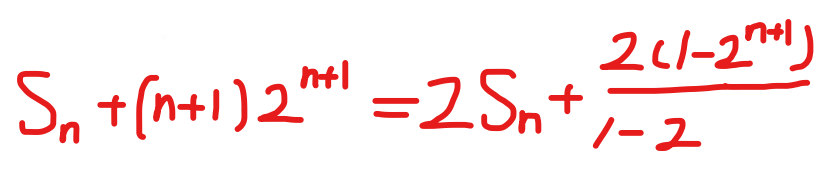
差分算子，上升和下降阶乘幂和差分法求解
差分算子△
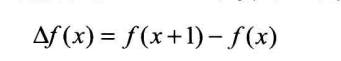
下降阶乘幂
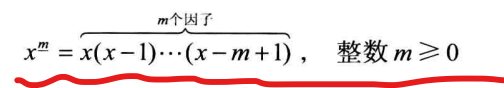
上升阶乘幂
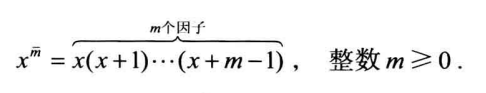
必须掌握（特别注意这里是x+1的下降阶次幂）
微分对应差分，积分对应离散求和
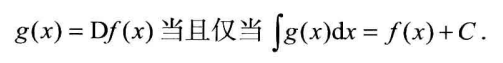
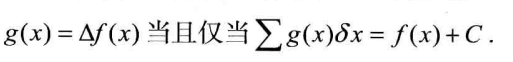
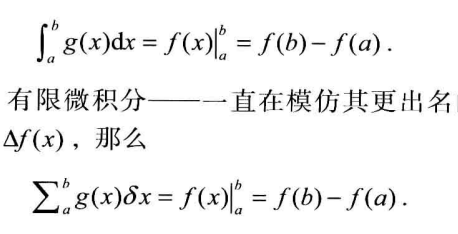
注意其上下界限
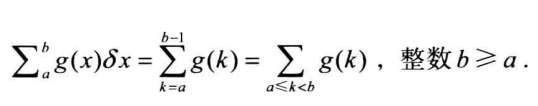
例子：
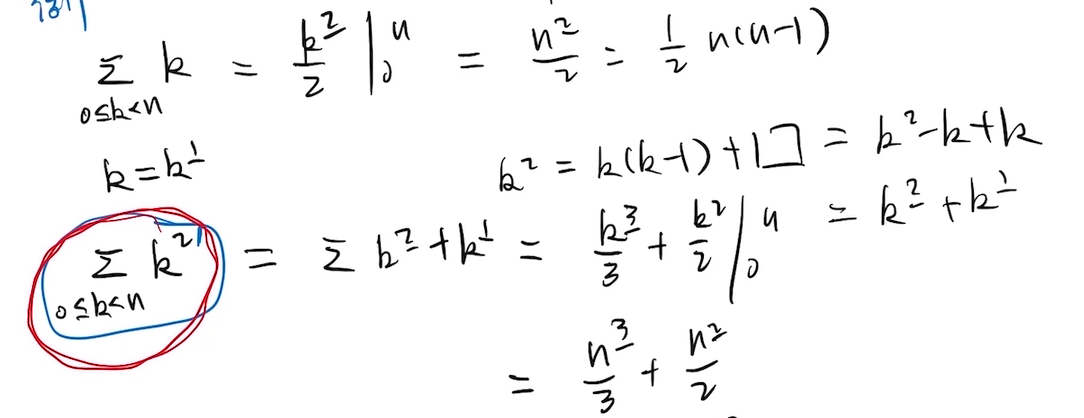
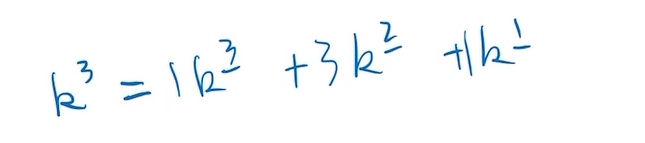
但是遇到正常的幂次需要转换为阶乘幂
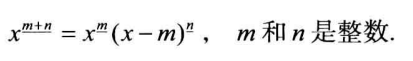
差分法求解和式（即利用分部求和法则） 重点！
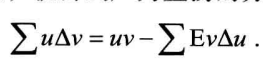
重点：
扫一扫
1880
到【灌水乐园】发言
